Решение задач планиметрии
1.задание
Тема:
|
Координаты вектора.
|
Цель обучения:
|
9.1.3.1 находить координаты вектора;
9.1.3.2 находить длину вектора;
|
Условие задачи:
|
Заданы векторы: 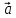 =(-3;5) и =(-3;5) и 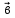 =(0;-1) =(0;-1)
Найдите координаты вектора:
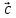 = = 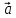 + + 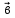
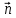 = = 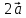 + + 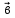
Найдите длину вектора 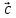
|
Решение:
|
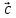 = = 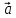 + + 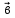 =(-3+0; 5+(-1)) = (-3; 4) =(-3+0; 5+(-1)) = (-3; 4)
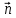 = = 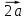 + + 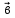 =(2 =(2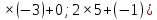 = (-6; 9) = (-6; 9)
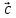 = = 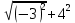 = = 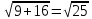 =5 (ед) =5 (ед)
|
Ответ:
|
(-3; 4)
(-6; 9)
5 ед.
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для формативного оценивания, для проверки усвоения формул.
|
2.задание
Тема:
|
Применение векторов к решению задач.
|
Цель обучения:
|
9.1.4.19 применять векторы к решению задач;
|
Условие задачи:
|
Даны координаты точек С(3; -2), Д(-1; 2), М(2; -3), N(-1; 1). Найдите косинус угла между векторами 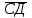 и и 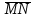 . .
|
Решение:
|
cosα= 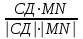
CД(-4;4) 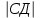 = =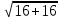 =4 =4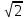
MN=(-3;4) 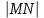 = = 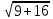 =5 =5
Cosα =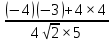 = = 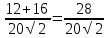 = = 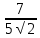
|
Ответ:
|
Cosα =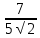
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для работы в группе или парах при закреплении материала, при формативном оценивании.
|
3.задание
Тема:
|
Применение векторов к решению задач.
|
Цель обучения:
|
9.1.4.19 применять векторы к решению задач;
|
Условие задачи:
|
При каком значении n данные векторы перпендикулярны:
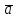 (2; 3) и (2; 3) и 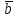 (1; n)? (1; n)?
|
Решение:
|
Векторы перпендикулярны, когда их скалярное произведение равно нулю.
ab=2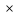 1+3n 1+3n
3n+2=0
3n=-2
n=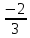
|
Ответ:
|
- 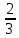
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при проверке понимания перепендикулярности векторов при формативном оценивании.
|
4.задание
Тема:
|
Решение треугольников
|
Цель обучения:
|
9.1.3.10 применять теоремы синусов и косинусов для решения треугольников и прикладных задач I
|
Условие задачи:
|
Задача.
Два парохода начинают движение одновременно из одного и того же пункта и двигаются равномерно по прямым пересекающимся под углом 600. Скорость первого 40км/ч, второго – 30км/ч. Вычислите , на каком расстоянии друг от друга будут находиться пароходы через 3 часа?
|
Решение:
|
Решение:
V1= 40 км/ч , то S1= АС =120 км
V2 = 30км/ч, то S2= АВ =90 км
Найдем расстояние ВС по теореме косинусов:
ВС2= АС2+ АВ2– 2АС АВ*cos600
ВС2=1202+ 902- 2*120*90*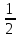
ВС2=14400 + 8100 – 10800
ВС2 =11700; ВС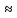 108 108
|
Ответ:
|
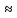 108 км 108 км
|
Методические рекомендации по использованию на уроке:
|
При изучении материала
|
5.задание
Тема:
|
Решение треугольников
|
Цель обучения:
|
9.1.3.10 применять теоремы синусов и косинусов для решения треугольников и прикладных задач I
|
Условие задачи:
|
Задача.
В 7 часов утра пассажирский самолёт вылетел из города А. После получасовой остановки в городе В в 8 часов 10 минут самолёт сделал поворот на 35вправо и в 9 часов совершил посадку в городе С.
Найти расстояние между городами А и С, если средняя скорость самолёта на каждом участке полёта была равна 320км/час.
|
Решение:
|
Да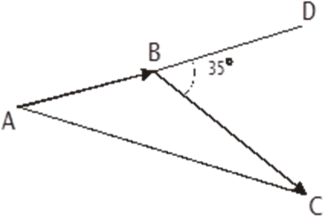 но:СВD = 35, но:СВD = 35,
v = 320 км/час, t1 = 7 ч.,
t2= 8 ч. 10 мин,t3= 9 ч.
tост= 30 мин.
Найти АС.
Решение:
АВ= v*( t2 – t1 – t0 )=320*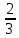 = = 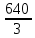 (км) (км)
ВС= v*( t3 – t2)=320*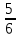 = = 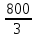 (км) (км)
АВС +DВС = 180(как смежные)
АВС = 180– 35, АВС = 145
Из треугольника АСВ по теореме косинусов находим АС:
АС2= АВ2+ ВС2– 2АВ * ВС*cos145= 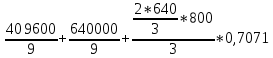 458 км 458 км
|
Ответ:
|
АС 458 км.
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала.
|
6.задание
Тема:
|
Применение векторов к решению задач.
|
Цель обучения:
|
9.1.4.19 применять векторы к решению задач
|
Условие задачи:
|
Задача.
Парашютист спускался со скоростью 3м/с. Ветром его начинает сносить в сторону со скоростью 3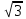 м/с. Какова его реальная скорость? Под каким углом к вертикали спускается парашютист? м/с. Какова его реальная скорость? Под каким углом к вертикали спускается парашютист?
|
Решение:
|
Скорость парашютиста v0= 3 м/с, скорость ветра vв = 3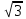 м/с. Скорость – векторная величина. Т. к. парашютист имеет две скорости в различных направлениях, то результирующая (истинная скорость) находится как векторная сумма первых двух: м/с. Скорость – векторная величина. Т. к. парашютист имеет две скорости в различных направлениях, то результирующая (истинная скорость) находится как векторная сумма первых двух:
Найдем ее, используя правило параллелограмма (в нашем случае параллелограмм – это прямоугольник (см. рис.)
,
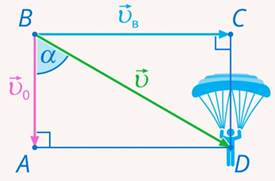
Прямоугольник АВСD. Значение реальной скорости – это длина вектора, т. е. диагонали прямоугольника:
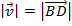
Ее можно найти, используя теорему Пифагора:
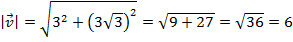
Тангенс искомого угла между вертикалью и реальной скоростью равен, по определению, отношению противолежащего катета к прилежащему:
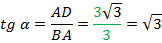
Острый угол, который соответствует такому тангенсу, равен 600.
|
Ответ:
|
6 м/с; 600
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
7.задание
Тема:
|
Вектор. Действия над векторами. Коллинеарные и неколлинеарные векторы
|
Цель обучения:
|
9.1.4.2 знать и применять правила сложения векторов и умножения вектора на число
9.1.4.3 применять условие коллинеарности векторов;
|
Условие задачи:
|
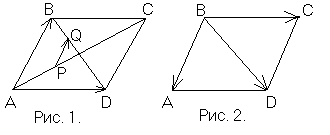
В параллелограмме ABCD диагонали AC и BD разделены в отношении 1:2 и 2:3 соответственно точками 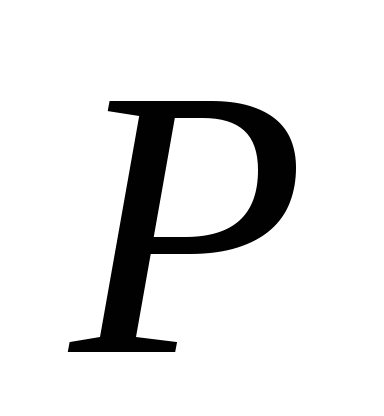 и и  . Разложить вектор . Разложить вектор  по векторам по векторам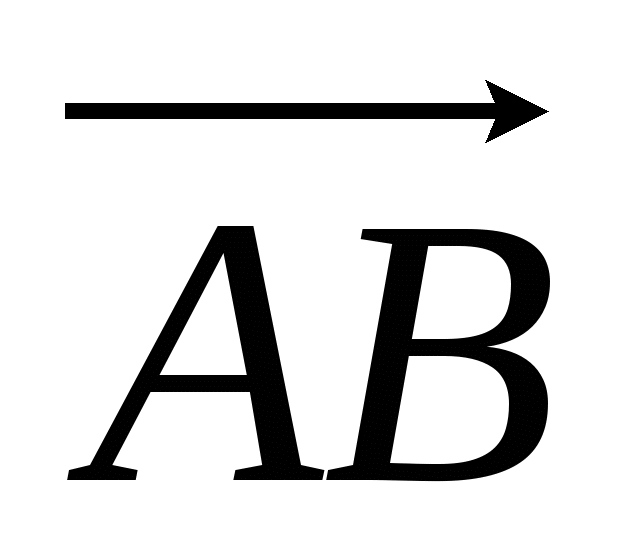 и и . (Рис.1.) . (Рис.1.)
|
Решение:
|
Используя правило сложение векторов, выразим векторы  и и через векторы через векторы 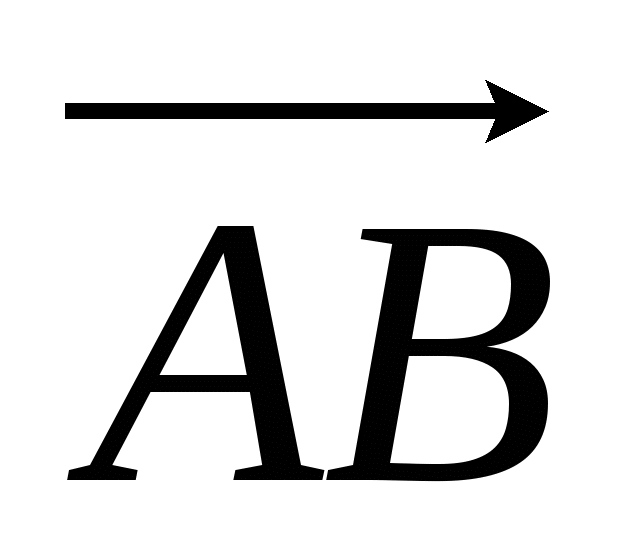 и и  следующим образом: следующим образом:
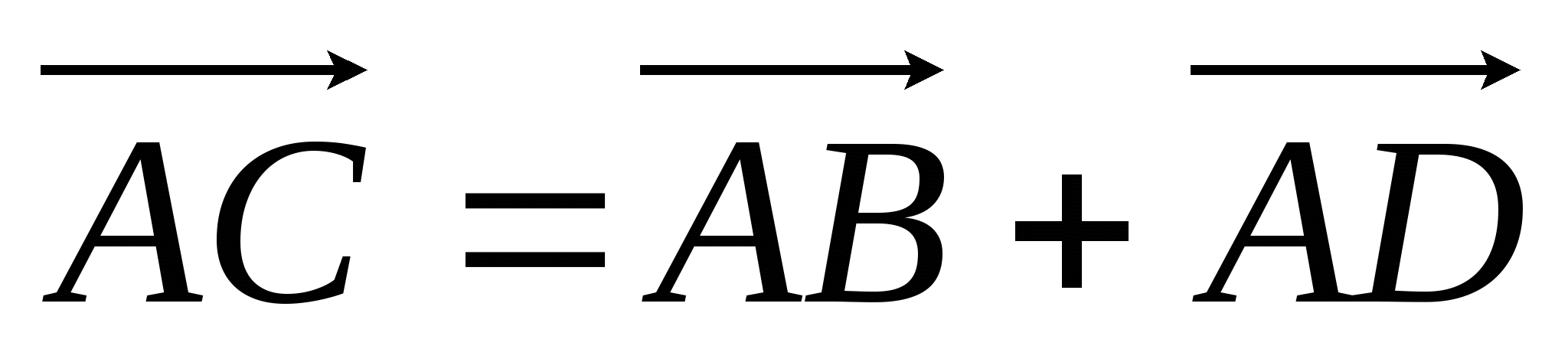 ; ;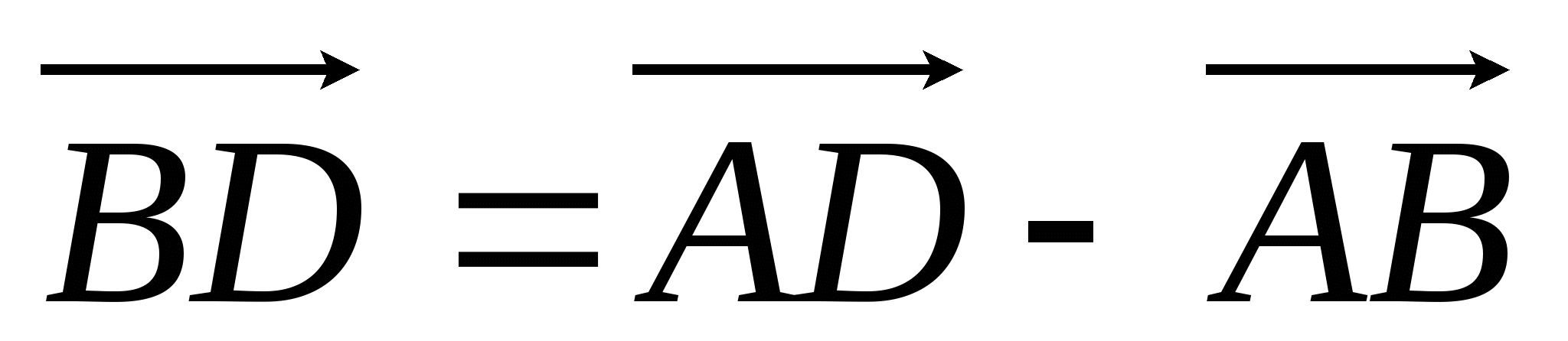 . .
Векторы 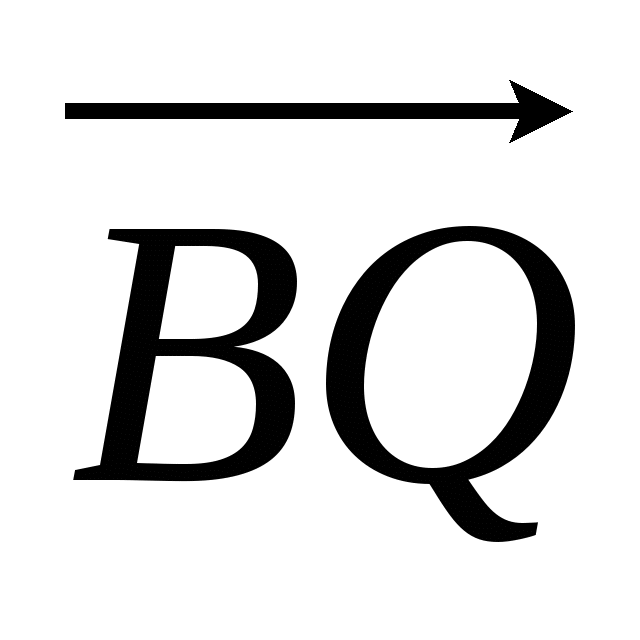 и и  коллинеарны векторам коллинеарны векторам  и и  соответственно, поэтому соответственно, поэтому
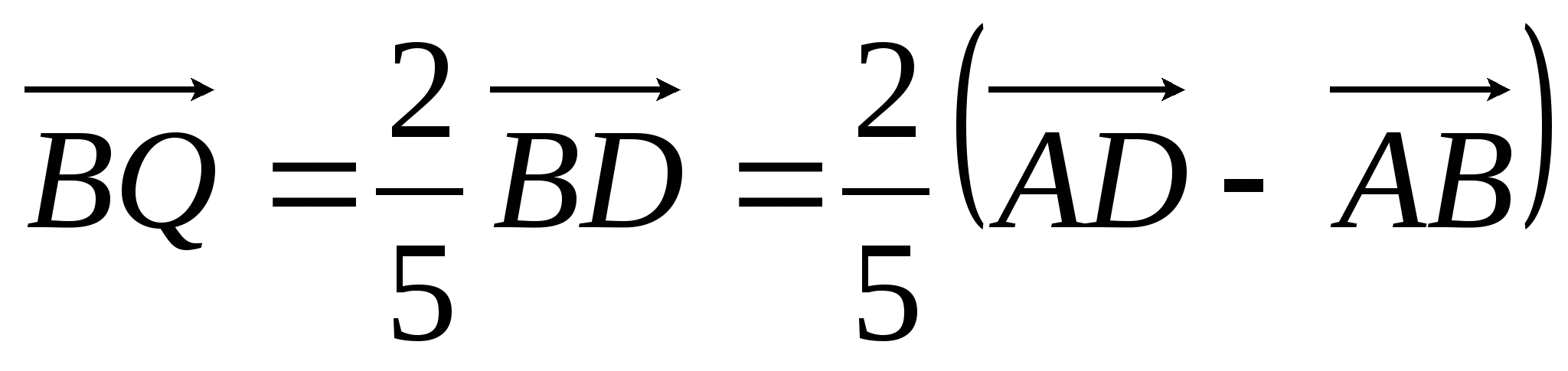 , , 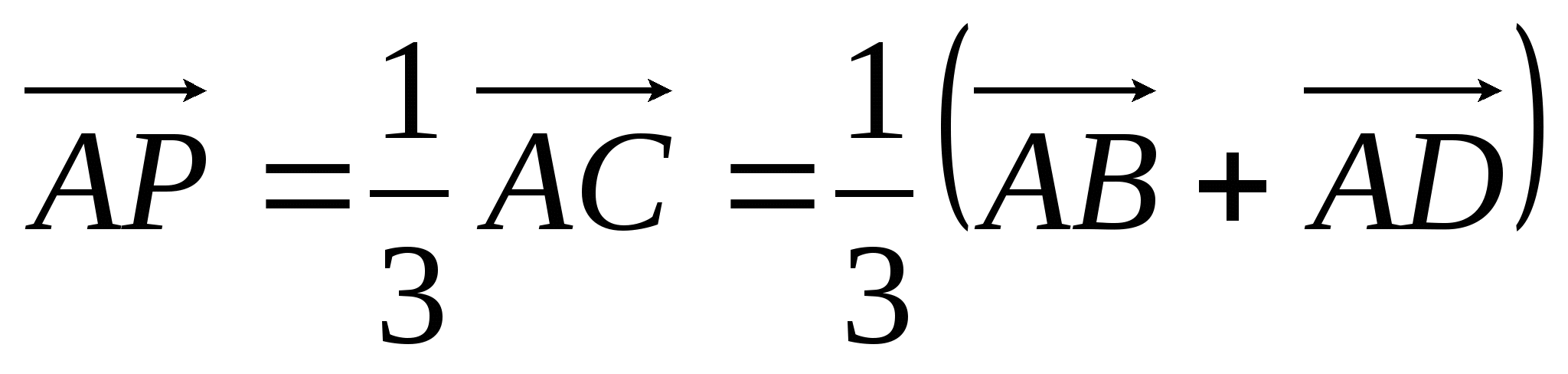 . .
В четырехугольнике ABQP можно записать следующее соотношение: 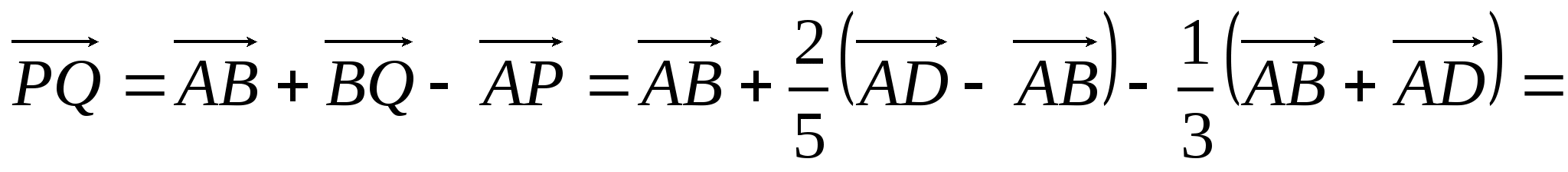
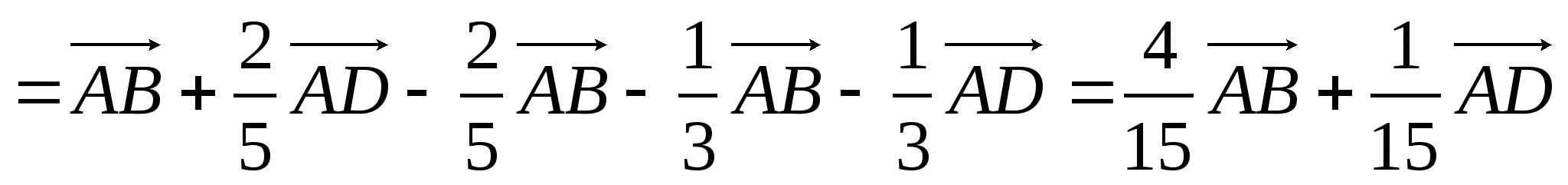 . .
Ответ: 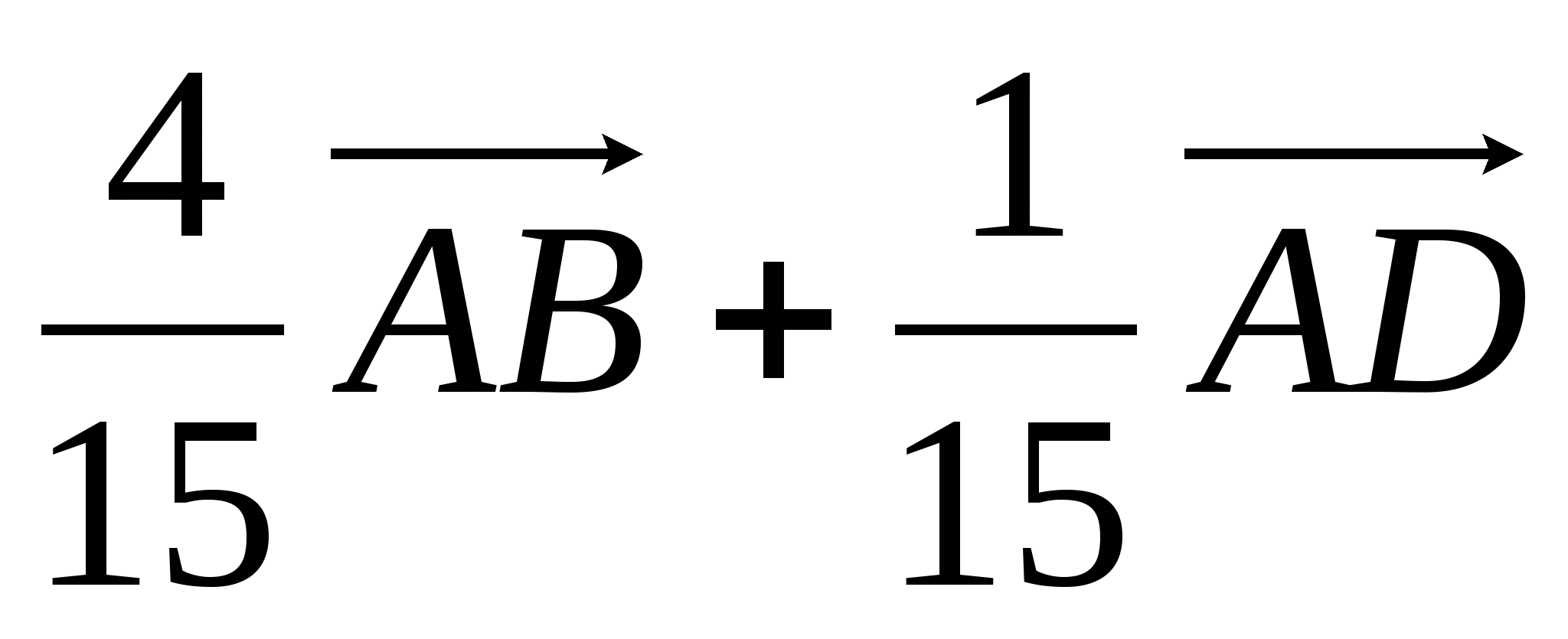 . .
|
Ответ:
|
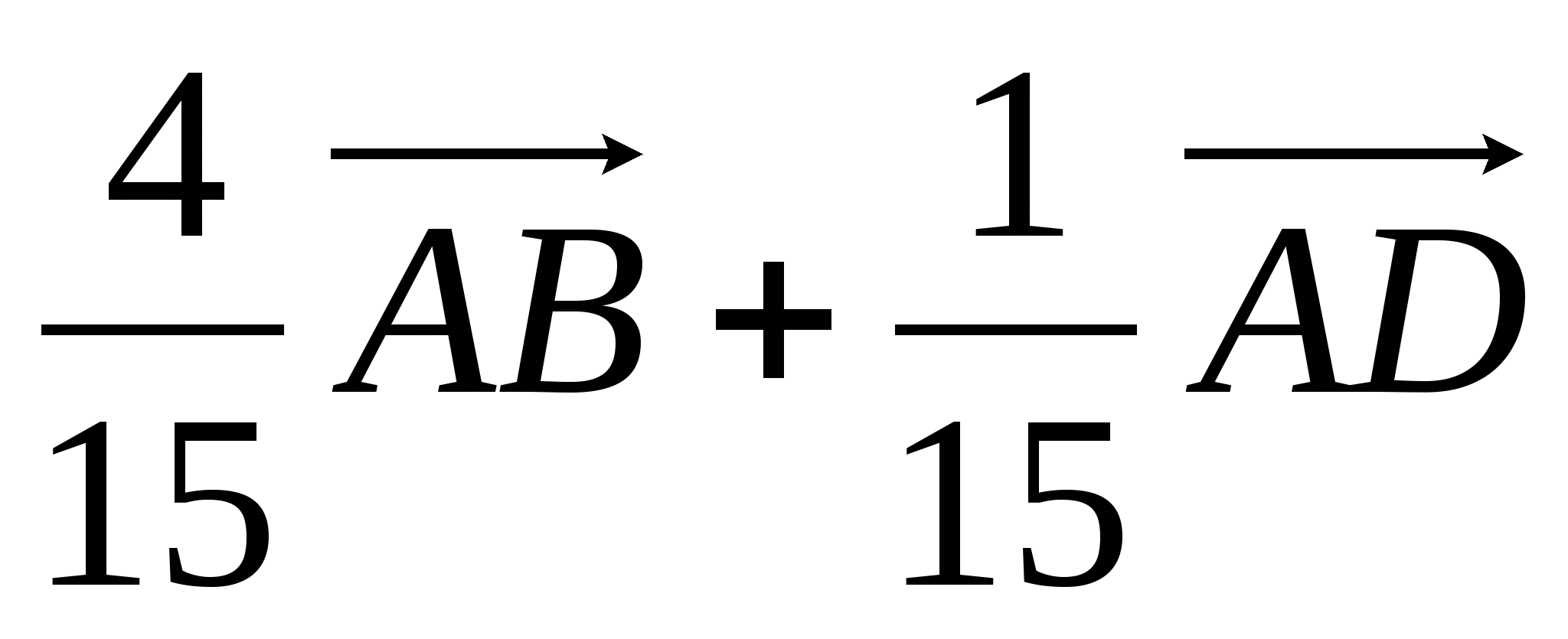
|
Методические рекомендации по использованию на уроке:
|
Предложить для самостоятельной работы учащимся
|
8.задание
Тема:
|
Окружность, круг, их элементы и части. Центральный угол
|
Цель обучения:
|
7.1.1.29 знать и применять определение и свойства центрального угла;
|
Условие задачи:
|
Колесо имеет 15 спиц. Найдите величину угла в градусах, который образует две соседние спицы.
|
Решение:
|
Окружность составляет 3600.
Спиц по условию задачи у нас 15, они делят окружность на 15 равных секторов.
360:15=240 – величина угла каждого сектора
|
Ответ:
|
240
|
Методические рекомендации по использованию на уроке:
|
Задача прикладного характера на понимание темы «Центральный угол. Окружность»
Предложить учащимся в тестах на закрепление пройденного материала
| |
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
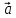 =(-3;5) и
=(-3;5) и 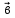 =(0;-1)
=(0;-1)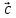 =
= 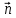 =
= 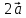 +
+ 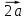 +
+ 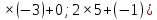 = (-6; 9)
= (-6; 9)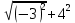 =
= 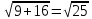 =5 (ед)
=5 (ед)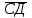 и
и 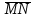 .
.
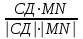
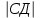 =
=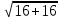 =4
=4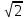
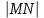 =
= 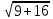 =5
=5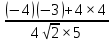 =
= 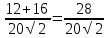 =
= 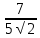
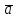 (2; 3) и
(2; 3) и 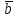 (1; n)?
(1; n)?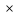 1+3n
1+3n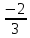
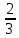
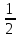
 108
108 но:СВD = 35,
но:СВD = 35,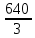 (км)
(км)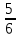 =
= 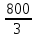 (км)
(км)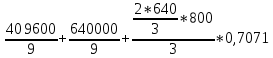 458 км
458 км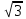 м/с. Какова его реальная скорость? Под каким углом к вертикали спускается парашютист?
м/с. Какова его реальная скорость? Под каким углом к вертикали спускается парашютист?
