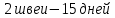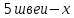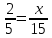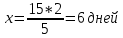|
|
задания по МОДО. ИтоговаяРабота - 4 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
ИТОГОВАЯ РАБОТА
по обучению на курсе повышения квалификации
«Развитие предметных компетенций учителей математики»
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
для учителей математики общеобразовательных школ
Критерии оценки:
Задачи соответствуют целям/цели обучения.
Задачи носят практико-ориентированный характер.
Представлены верные решения задач.
Оформлены ответы.
Представлены методические рекомендации по использованию задач на уроке.
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
для учителей математики общеобразовательных школ
Данный сборник содержит методические рекомендации для учителей математики общеобразовательных школ. В сборник включены образцы решения задач по тематике курса. Задачи составлены в соответствии с целями обучения предметов "Математика", «Алгебра», «Алгебра и начала анализа», «Геометрия».
Выполнила группа:
Макашева Айсулу Саметовна
Ташкен Жанна Серікқызы
Мукеева Жанат Мукановна
Тусупова Елена Мурзахметовна
СОДЕРЖАНИЕ
|
стр
|
Методы решения текстовых задач
|
5
|
Решение задач на нахождение процента от числа
Прямая и обратная пропорциональная зависимость.
Решение текстовых задач с помощью пропорции.
Задачи на нахождение масштаба, длины окружности, площади круга.
|
|
|
|
Методы решения задач по статистике и теории вероятностей в основной школе
|
|
Абсолютная и относительная частота
Бином Ньютона и его свойства.
Элементы комбинаторики.
Решение задач с использованием формул комбинаторики.
|
12
|
Методы решения задач на событие и вероятность.
|
|
Элементы математической статистики.
Вариационные ряды.
|
|
Прикладные задачи на математическое моделирование и анализ
|
|
Прикладные задачи на исследование квадратичных функций.
|
19
|
Текстовые задачи на прогрессии
|
|
|
|
Решение задач планиметрии
|
28
|
Решение треугольников.
|
|
Векторы на плоскости. Применение векторов в решении геометрических задач
|
|
Преобразования плоскости. Методы решения задач с применением преобразований плоскости
|
|
Окружность, круг и их элементы. Центральный угол
Решение задач стереометрии
|
|
Многогранники. Сечения многогранников плоскостями
Способы решения задач на нахождение площади боковой и полной поверхности пространственных фигур.
|
37
|
Методы решения задач на нахождение элементов тел вращения и объемов пространственных фигур
|
|
Комплексные числа. Основная теорема алгебры
|
|
Комплексные числа. Арифметические действия над комплексными числами
|
45
|
Комплексная плоскость. Модуль комплексного числа
|
|
Решение квадратных уравнений на множестве комплексных чисел.
|
|
Методы решения уравнений и неравенств в старшей школе
|
52
|
Решение уравнений высших степеней различными методами. Применение обобщенной теоремы Виета к многочленам третьего порядка
|
|
Методы решения иррациональных уравнений и неравенств
|
|
Методы решения тригонометрических уравнений и неравенств
|
|
Решение систем логарифмических, показательных уравнений и неравенств
|
|
Статистика и теория вероятностей в старших классах
|
59
|
Вероятность события и ее свойства. Правила сложения и умножения вероятностей
|
|
Задачи на нахождение вероятностей с применением формулы комбинаторики.
Применение бинома Ньютона для приближённых вычислений
|
|
Формула полной вероятности.
Применение формулы Байеса при решении задач.
Формула Бернулли и ее следствия
|
|
Прикладные задачи на математическое моделирование и анализ в старших классах
|
66
|
Прикладные задачи на применение физического и геометрического смысла производной
|
|
Прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
|
Применение определенного интеграла для решения физических задач на вычисление работы и расстояния
|
|
|
|
|
|
|
|
Методы решения текстовых задач
1.задание
Тема:
|
Длина окружности.
|
Цель обучения:
|
6.3.3.2 знать, что отношение длины окружности к ее диаметру есть число постоянное;
6.3.3.3 знать и применять формулу длины окружности;
|
Условие задачи:
|
Радиус круга равен 5 см. Найдите длину окружности С. (число π округлите до одного знака после запятой)
|
Решение:
|
С = 2πR
π =3,14… 3,1 3,1
С= 2 ∙ 3,1 ∙ 5 = 31 (см).
|
Ответ:
|
Ответ: 31 см;
|
Методические рекомендации по использованию на уроке:
|
Использовать для повторения округления чисел(округление числа π)
Для закрепления при применении формулы длины окружности.
|
2.задание
Тема:
|
Нахождение процентов от данного числа
|
Цель обучения:
|
5.1.2.34 - находить процент данного числа;
5.1.2.35 - находить процентное отношение одного числа к другому и наоборот;
|
Условие задачи:
|
В 6 «А» классе 25 человек. 80% всех учеников по окончанию учебного года отправятся в поход. Сколько учеников отправились в поход?
|
Решение:
|
80%=0,8
25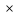 0,8=20(уч) отправятся в поход 0,8=20(уч) отправятся в поход
|
Ответ:
|
20 учеников
|
Методические рекомендации по использованию на уроке:
|
Использовать при закрепление навыков перевода процентов в десятичное число и при нахождении процентов от числа
|
3.задание
Тема:
|
Площадь круга.
|
Цель обучения:
|
6.3.3.3 знать и применять формулу длины окружности;
6.3.3.4 знать и применять формулу площади круга;
|
Условие задачи:
|
Вычислите площадь заштрихованных фигур (сторона клетки равна 1см)
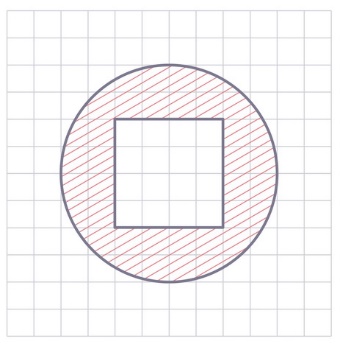
|
Решение:
|
S = πR2
R=4 см
Sкруга = 3,14 ∙ 42 = 3,14 ∙ 16 = 50,24 (см2).-площадь круга
а=4см-сторона квадрата
S = а2 = 42 = 16 (см2).-площадь квадрата
S = 50,24 – 16 = 34,24 (см2).-площадь заштрихованной фигуры
|
Ответ:
|
S = 34,24 см2.
|
Методические рекомендации по использованию на уроке:
|
Использовать при решении задач на нахождении площади круга, при повторении площади квадрата, определении радиуса круга и стороны квадрата по рисунку.
|
4.задание
Тема:
|
Решение текстовых задач с помощью пропорции
|
Цель обучения:
|
6.5.1.2 решать задачи на проценты с помощью пропорции;
|
Условие задачи:
|
Задача.
Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?
|
Решение:
|
Примем всех подписчиков за 100% и запишем условие задачи кратко:
300ч. — 100%
108 ч.— x %
Составим пропорцию: 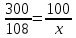 ; ;
Найдем х:
х= (108 * 100) : 300 = 36.
|
Ответ:
|
Ответ: 36% всех подписчиков поставили лайк под постом.
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
5.задание
Тема:
|
Решение текстовых задач с помощью пропорции
|
Цель обучения:
|
6.1.2.6 делить величины в заданном отношении;
|
Условие задачи:
|
Отец с сыном собрали 18 кг яблок, причем отец собрал в 2 раза больше яблок, чем сын. Сколько килограммов яблок собрал каждый из них?
|
Решение:
|
Решение: Поскольку отец собрал в 2 раза больше яблок, то количество собранных отцом и сыном яблок находится в отношении 2 : 1 . Значит, нужно 18 кг разделить на две части, отношение которых равно 2 : 1.
|
Яблок, кг
|
Часть
|
Всего
|
18
|
2+1=3
|
Отец
|
x
|
2
|
Сын
|
y
|
1
|
Составим пропорции: 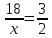 ; ; 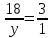 . .
Решая пропорции, найдем значения x - яблок в килограммах, собранных отцом;
y - яблок в килограммах, собранных сыном.
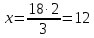 (кг) яблок собрал отец; (кг) яблок собрал отец;
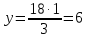 (кг) яблок собрал сын. (кг) яблок собрал сын.
|
Ответ:
|
Ответ: 12 кг, 6 кг.
|
Методические рекомендации по использованию на уроке:
|
При изучении нового материала
|
6.Задание
Тема:
|
Прямая пропорциональная зависимость. Обратная пропорциональная зависимость
|
Цель обучения:
|
6.5.1.1 распознавать и решать задачи, в которых величины связаны прямой и обратной пропорциональностями
|
Условие задачи:
|
Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
|
Решение:
|
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится. Обозначим:
v1= 75 км/ч, t1 = 13 ч
v2 = 52 км/ч, t2 = х
Составим пропорцию: 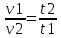 . .
Подставим известные значения: 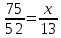 . .
х = : 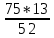 = = 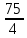 = 18 = 18 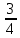 = 18 ч 45 мин = 18 ч 45 мин
|
Ответ:
|
Ответ: 18 часов 45 минут.
|
Методические рекомендации по использованию на уроке:
|
При изучении нового материала
|
7. задание
Тема:
|
Решение текстовых задач с помощью пропорции
|
Цель обучения:
|
6.5.1.2 решать задачи на проценты с помощью пропорции;
|
Условие задачи:
|
Собрав урожай картофеля, дачник проанализировал, что 16% картофеля было маленького размера, среднего – на 47% больше, чем маленького, а остальные - большого размера. Сколько тонн картофеля большого размера собрал дачник, если весь урожай составил 10 тонн?
|
Решение:
|
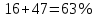 - картофеля среднего размера - картофеля среднего размера
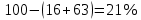 - картофеля большого размера - картофеля большого размера
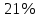 − х − х
 − 10 т − 10 т
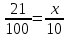
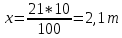
|
Ответ:
|
2,1 тонн
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
8. задание
Тема:
|
Прямая пропорциональная зависимость. Обратная пропорциональная зависимость
|
Цель обучения:
|
6.5.1.1 распознавать и решать задачи, в которых величины связаны прямой и обратной пропорциональностями;
|
Условие задачи:
|
Купив в магазине 10 метров ткани, мама сшила двум дочерям близняшкам по 3 платья. Если потребуется сшить 9 таких платьев, то сколько метров ткани потребуется?
|
Решение:
|
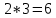 – платьев сшила мама – платьев сшила мама
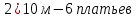
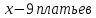
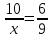
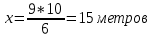
|
Ответ:
|
15 метров
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для формативного оценивания.
|
9. задание
Тема:
|
Прямая пропорциональная зависимость. Обратная пропорциональная зависимость
|
Цель обучения:
|
6.5.1.1 распознавать и решать задачи, в которых величины связаны прямой и обратной пропорциональностями;
|
Условие задачи:
|
2 швеи вместе выполняют заказ за 15 дней. За сколько дней справятся швеи, если им помогут еще 3 швеи?
|
Решение:
|
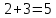 швей швей
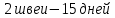
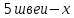
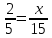
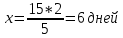
|
Ответ:
|
6 дней
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для формативного оценивания.
|
10.задание
Тема:
|
Решение задач на проценты способом пропорции
|
Цель обучения:
|
6.5.1.2 решать задачи на проценты с помощью пропорции;
|
Условие задачи:
|
Цена на школьные пеналы по акции «Уценка товара» была снижена на 50 тенге. Изначально пенал стоил 300 тенге. На сколько процентов нужно поднять новую цену пенала, чтобы вернуться к старой цене в 300 тенге?
|
Решение:
|
После уценки пенал стоит 300-50=250 тенге.
250 тенге – это новая цена товара – 100%
300 тенге – это желаемая цена товара – х%
Составим и решим пропорцию:
250-100%
300-х%
Х=(300*100)/250
Х= 120%
300-120%, значит повысили на 20%
|
Ответ:
|
20%
|
Методические рекомендации по использованию на уроке:
|
вопросы:
Какова новая цена пенала?
Что возьмём за 100%?
Что означает 120% ?
|
11.задание
Тема:
|
Решение задач на проценты способом пропорции
|
Цель обучения:
|
6.5.1.2 решать задачи на проценты с помощью пропорции;
|
Условие задачи:
|
В магазине на определённый товар предоставили скидку 17%. Если цена товара после скидки стала 1245 тенге, то чему равна его изначальная цена ?
|
Решение:
|
Если изначальная стоимость бвла 100%, то после скидки на 17% получаем 100-17=83% это 1245 тенге
Составим и решим пропорцию:
Х - 100%
1245 – 83% Х=1245*100:83
Х= 1500 (тенге) изначальная цена
|
Ответ:
|
1500 тенге
|
Методические рекомендации по использованию на уроке:
|
Задачу можно предложить в качестве самостоятельной работы
|
12.задание
Тема:
|
Текстовые задачи
|
Цель обучения:
|
6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений;
|
Условие задачи:
|
Если банка полна на 20%, она содержит на 3 литра меньше варенья, чем когда она пуста на 20%. Сколько литров варенья вмещает банка?
|
Решение:
|
Пусть Х- вместимость банки, тогда банка полна на 20% = 0,2х и
банка пуста на 20% (значит полна на 80%) = 0,8х.
По условию задачи банка, наполненная на 20%, содержит на 3 литра меньше варенья, чем банка наполненная на 80%.
Составим и решим уравнение: 0,8х-0,2х=3
0,6х=3
Х=5 (литров)
|
Ответ:
|
5 литров
|
Методические рекомендации по использованию на уроке:
|
Задачу можно предложить в качестве самостоятельной работы
Если ученики не будут справляться, можно предложить по шаговую инструкцию с рисунком .
20%
20%
|
|
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
 3,1
3,1 0,8=20(уч) отправятся в поход
0,8=20(уч) отправятся в поход
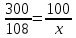 ;
; 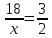 ;
; 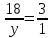 .
.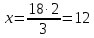 (кг) яблок собрал отец;
(кг) яблок собрал отец; 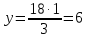 (кг) яблок собрал сын.
(кг) яблок собрал сын.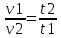 .
.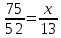 .
.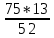 =
= 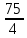 = 18
= 18 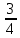 = 18 ч 45 мин
= 18 ч 45 мин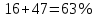 - картофеля среднего размера
- картофеля среднего размера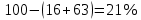 - картофеля большого размера
- картофеля большого размера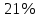 − х
− х − 10 т
− 10 т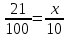
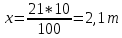
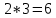 – платьев сшила мама
– платьев сшила мама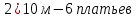
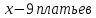
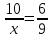
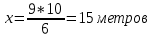
 швей
швей