|
|
задания по МОДО. ИтоговаяРабота - 4 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
9.задание
Тема:
|
Многоранники
|
Цель обучения:
|
11.3.3 - решать задачи на нахождение элементов многогранников
|
Условие задачи:
|
В правильной треугольной пирамиде со стороной основания 12см и боковыми ребрами по 10 см найти угол, образованный боковым ребром и плоскостью основания пирамиды;
|
Решение:
|
Высота правильного треугольника АН по формуле: h=а*√3/2, где а - сторона треугольника.
AH=12√3/2 = 6√3см.
В правильном треугольнике высота=медиана=биссектриса. По свойству медианы (центром правильного треугольника делится в отношении 2:1, считая от вершины).
АО=(2/3)*h = 4√3см. OH=2√3см.
По Пифагору: SO=√(AS²-AO²) = √(100-48) = 2√13см.
|
Ответ:
|
2√13см
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
10.задание
Тема:
|
Многоранники
|
Цель обучения:
|
11.3.18 - решать задачи
практического содержания на комбинации геометрических тел
|
Условие задачи:
|
Основание садового домика — прямоугольник 6×8 (м). Крыша наклонена под углом 45◦ к основанию. Найдите сколько 2кг банок краски потребуется на покраску крыши, если на 1м2 расходуется 100г. краски.
|
Решение:
|
AD=8 м, CD=6м, угол SEO=450, тогда площадь крыши S=6*8* cos 450= 48 cos 45◦ = 48*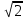 ≈67,9 (м2 ). ≈67,9 (м2 ).
67,9*100:1000=6,79
|
Ответ:
|
7 банок
|
Методические рекомендации по использованию на уроке:
|
Для ф.о.
|
11.задание
Тема:
|
Сечения многогранников плоскостями
|
Цель обучения:
|
11.2.1 - уметь строить сечения многогранника плоскостью.
|
Условие задачи:
|
Высота МО правильной четырехугольной пирамиды МАВСD равна стороне квадрата АВ. Постройте сечение пирамиды плоскостью, проходящей через вершину А перпендикулярно ребру МС.
|
Решение:
|
В правильной пирамиде основание высоты находится в центре основания пирамиды, поэтому проекции её рёбер совпадают с отрезками диагоналей квадрата.
В плоскости AMC строим AH⊥MC. Из точки Н на гранях MDC и MBC восстанавливаем перпендикуляры HP и HR, соответственно. Достраиваем отрезки AP и AR. Четырёхугольник APHR искомое сечение (Т9).
|
Ответ:
|
APHR искомое сечение.
|
Методические рекомендации по использованию на уроке:
|
Урок закрепления.
|
12.задание
Тема:
|
Обьем комбинации геометрических тел.
|
Цель обучения:
|
11.2.5 - изображать комбинации геометрических тел на плоскости;
|
Условие задачи:
|
Середина ребра куба со стороной 1,8 является центром шара радиуса 0,9. Найдите объем части шара, лежащего внутри куба.
|
Решение:
|
Так как середина ребер куба является центром шара, диаметр которого равен ребру куба, в кубе содержится 1/4 шара, и, соответственно, 1/4 его объема. Имеем:
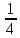 Vш= Vш=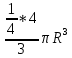 = = 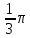 0,93 = 0,243 0,93 = 0,243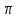 (ед.3) (ед.3)
|
Ответ:
|
0,243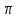 ед.3 ед.3
|
Методические рекомендации по использованию на уроке:
|
Для ф.о.
|
Комплексные числа. Основная теорема алгебры
1.задание
Тема:
|
Действия над комплексными числами в алгебраической форме
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме
|
Условие задачи:
|
Выполните умножение (2 + 3i) (5 – 7i).
|
Решение:
|
1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i =
= (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) =
= 10 – 14i + 15i + 21 = 31 + i
|
Ответ:
|
31 + i.
|
Методические рекомендации по использованию на уроке:
|
Для самостоятельного решения
|
2.задание
Тема:
|
Комплексные корни квадратных уравнений
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел
|
Условие задачи:
|
Решите уравнения:
а) x2 – 6x + 13 = 0; б) 9x2 + 12x + 29 = 0.
|
Решение:
|
а) Найдем дискриминант по формуле
D = b2 – 4ac.
Так как a = 1, b = – 6, c = 13, то
D = (– 6)2 – 4×1×13 = 36 – 52 = – 16;
Корни уравнения находим по формулам
б) Здесь a = 9, b = 12, c = 29. Следовательно,
D = b2 – 4ac =122 – 4×9×29 = 144 – 1044 = – 900,
Находим корни уравнения:
Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня
|
Ответ:
|
и
|
Методические рекомендации по использованию на уроке:
|
На закрепление темы
|
3.задание
Тема:
|
Действия над комплексными числами в алгебраической форме
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме
|
Условие задачи:
|
Найти частное
|
Решение:
|
1 способ.
2 способ.
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Для работы в группе
|
4.задание
Тема:
|
Комплексные корни квадратных уравнений
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел;
|
Условие задачи:
|
Найдите все корни квадратного уравнения х2+2х+5=0
|
Решение:
|
х2+2х+5=0
D =22-4*5= 4-20=-16
х1=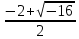 = = 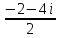 =-1- 2i =-1- 2i
х2=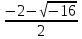 = =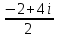 =-1+2i =-1+2i
|
Ответ:
|
-1- 2i; -1+2i
|
Методические рекомендации по использованию на уроке:
|
Можно использовать в групповой работе при закреплении
|
5.задание
Тема:
|
Действия над комплексными числами в алгебраической форме
|
Цель обучения:
|
- выполнять арифметические действия над комплексными числами в алгебраической форме;
- применять закономерность значения in при возведении в целую степень комплексного числа в алгебраической форме;
|
Условие задачи:
|
Найти сумму, разность, произведение и частное двух комплексных чисел z1=-9-7i и z2=-1 +i в алгебраической форме.
|
Решение:
|
z1+z2=-9-7i+(-1)+i= -10-6i
z1 - z2==-9-7i-(-1)-i = -8-8i
z1 *z2 =(-9-7i)( -1 +i)= 9-9i+7i-7i2 =9-2i+7=16-2i
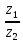 = = 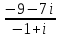 = =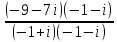 = = 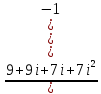 = = 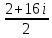 =1+8i =1+8i
|
Ответ:
|
-10-6i 16-2i
-8-8i 1+8i
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при формативном оценивании работу в группах или индивидуально.
|
6.задание
Тема:
|
Комплексные корни квадратных уравнений
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел;
|
Условие задачи:
|
Решить уравнения на множестве комплексных чисел:
а) 6х2+7=0 ;
|
Решение:
|
6х2+7=0 ;
6х2 = -7
х2= - 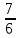
х1= 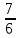 i i
x2= - 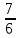 i i
|
Ответ:
|
х1= 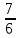 i i
x2= - 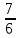 i i
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при проведении формативного оценивания
|
7.задание
Тема:
|
Комплексные числа
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме
|
Условие задачи:
|
Выполнить действия над комплексными числами в алгебраической форме:
(4-3i)+(-2+i)
(5+2i)-(3-i)
(7-2i)*(-7+i)
|
Решение:
|
(4-3i)+(-2+i)=2-2i
(5+2i)-(3-i)=2+3i
(7-2i)*(-7+i) = - 49+7i+14i+2= -47+21i
|
Ответ:
|
2-2i
2+3i
-47+21i
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
8.задание
Тема:
|
Комплексные числа
|
Цель обучения:
|
11.1.1.1 - знать определение комплексного числа и его модуля;
|
Условие задачи:
|
найти i28 , i 33 ,i 135 .
|
Решение:
|
28=4 * 7 (нет остатка)
33 = 4 * 8 + 1
135 = 4 * 33 + 3.
i28 = 1
i 33 = i
i 135 = - I
|
Ответ:
|
i28 = 1
i 33 = i
i 135 = - I .
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
9.задание
Тема:
|
Комплексные числа
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме
|
Условие задачи:
|
Найти частное
|
Решение:
|
|
Ответ:
|
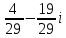
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
10.задание
Тема:
|
Действия над комплексными числами, заданными в алгебраической форме
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме;
|
Условие задачи:
|
Вычислить 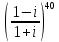 . Представить результат в алгебраической форме. . Представить результат в алгебраической форме.
|
Решение
|
Упростим выражение, умножая числитель и знаменатель на выражение, сопряженное знаменателю:
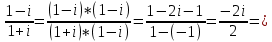 -i. -i.
Тогда z=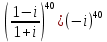 = ((-i)2)20 =(-1)20 =1. = ((-i)2)20 =(-1)20 =1.
Алгебраическая форма: z = 1= 1+0i .
|
Ответ:
|
z = 1= 1+0i .
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала для ф.о.
|
11.задание
Тема:
|
Действия над комплексными числами, заданными в алгебраической форме
|
Цель обучения:
|
11.1.2.1 - выполнять арифметические действия над комплексными числами в алгебраической форме;
|
Условие задачи:
|
Решить уравнение: 3x − (1− i)( x − yi) = 2 + 3i , x и y R.
|
Решение:
|
3x − (1− i)( x − yi) = 2 + 3i
3x − ( х− уi – хi + yi2) = 2 + 3i
3x − (( x − y) + (−x − y)i) = 2 + 3i
( 2x + y ) + ( x + y )i = 2 + 3i.
В силу равенства комплексных чисел имеем:
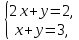
откуда x = –1 , y = 4
|
Ответ:
|
x = –1 , y = 4
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала для ф.о.
|
12.задание
Тема:
|
Комплексные корни квадратных уравнений
|
Цель обучения:
|
11.1.2.4 - решать квадратные уравнения на множестве комплексных чисел
|
Условие задачи:
|
Решить биквадратное уравнение на множестве комплексных чисел:
х4 + 14х2 + 53 = 0.
|
Решение:
|
Обозначим через х2=t, получаем t2 + 14t + 53 = 0.
D1= 49 – 53 = -4
t1,2 = -7 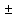 2i , x2== -7 ± 2i 2i , x2== -7 ± 2i
Решим уравнение x2 = -7 + 2i, учитывая, что комплексное число x= u +vi, где u и v – действительные числа: (u +vi)2=-7 + 2i.
u2 +2uvi – v2 =-7 + 2i.
Учитывая, что комплексные числа равны, если равны их действительные и мнимые части, получаем систему уравнений:
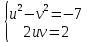 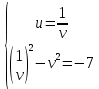
v4 – 7v2 -1 = 0, обозначим v2=a, получаем a2 -7a -1 =0. D=53
a1,2 =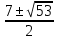 . Отсюда v2 = . Отсюда v2 =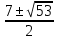 . Учитывая, что v – действительное число, оставляем положительное значение: v2 = . Учитывая, что v – действительное число, оставляем положительное значение: v2 =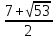 . .
Далее v1,2 =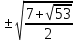 . Тогда u1,2 = . Тогда u1,2 =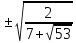 . .
Соответственно корни уравнения:
x1=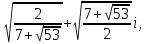 x2= x2=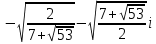 . .
После преобразования: x1=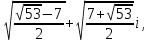 x2= x2=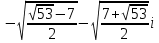 . .
Решим уравнение x2 = -7 - 2i, учитывая, что комплексное число x= u +vi, где u и v – действительные числа: (u +vi)2=-7 - 2i.
u2 +2uvi – v2 =-7 - 2i.
Учитывая, что комплексные числа равны, если равны их действительные и мнимые части, получаем систему уравнений:
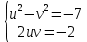 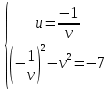
v4 – 7v2 -1 = 0, обозначим v2=a, получаем a2 -7a -1 =0. D=53
a1,2 =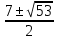 . Отсюда v2 = . Отсюда v2 =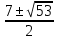 . Учитывая, что v – действительное число, оставляем положительное значение: v2 = . Учитывая, что v – действительное число, оставляем положительное значение: v2 =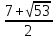 . .
Далее v3,4 =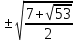 . Тогда u3,4 = . Тогда u3,4 =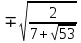 . .
Соответственно корни уравнения:
X3=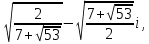 x4= x4=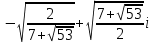 . .
После преобразования:
х3=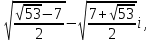 x4= x4=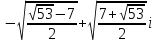 . .
|
Ответ:
|
x1=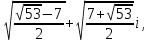 x2= x2=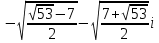 , х3= , х3=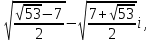 x4= x4=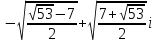 . .
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
|
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
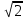 ≈67,9 (м2 ).
≈67,9 (м2 ).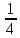 Vш=
Vш=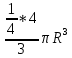 =
= 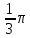 0,93 = 0,243
0,93 = 0,243 (ед.3)
(ед.3)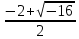 =
= 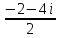 =-1- 2
=-1- 2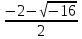 =
=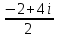 =-1+2i
=-1+2i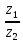 =
= 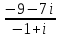 =
=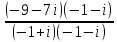 =
= 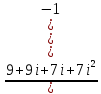 =
= 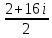 =1+8i
=1+8i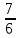
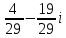
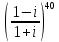 . Представить результат в алгебраической форме.
. Представить результат в алгебраической форме.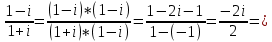 -i.
-i.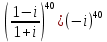 = ((-i)2)20 =(-1)20 =1.
= ((-i)2)20 =(-1)20 =1.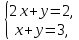
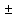 2i , x2== -7 ± 2i
2i , x2== -7 ± 2i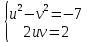
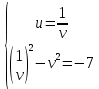
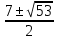 . Отсюда v2 =
. Отсюда v2 =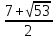 .
. 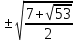 . Тогда u1,2 =
. Тогда u1,2 =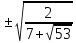 .
. 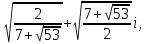 x2=
x2=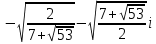 .
.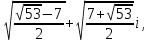 x2=
x2=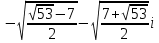 .
.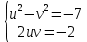
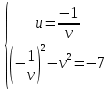
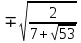 .
. 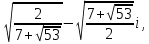 x4=
x4=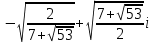 .
. 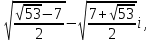 x4=
x4=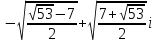 .
.