Прикладные задачи на математическое моделирование и анализ
1.задание
Тема:
|
Формула суммы первых n членов арифметической прогрессии
|
Цель обучения:
|
9.2.3.5 знать и применять формулы n-го члена, суммы n первых членов и характеристическое свойство арифметической прогрессии;
|
Условие задачи:
|
Численность населения города Астаны на начало 2015 года по данным КазСтат составила 852 тыс. жителей. Население города Астана увеличивается каждый год приблизительно на 45 тыс. жителей. Какова будет приблизительно численность населения Астаны:
а) к 2020 году? b) к 2030 году?
|
Решение:
|
852 тыс, 897 тыс,...-арифметическая прогрессия
а1 =852 тыс.
d=45
n=6, n=16
an=a1 +(n-1)d
a6 =852+5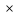 45=1077 тыс.(жителей) население в 2020году 45=1077 тыс.(жителей) население в 2020году
a16 =852+15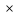 45=1527 тыс.(жителей) население в 2030 году 45=1527 тыс.(жителей) население в 2030 году
|
Ответ:
|
1077 тыс.жителей, 1527 тыс.жителей
|
Методические рекомендации по использованию на уроке:
|
|
2.задание
Тема:
|
Геометрическая прогрессия. Решение задач
|
Цель обучения:
|
9.2.3.7 решать задачи, связанные с геометрической прогрессией;
|
Условие задачи:
|
В геометрической прогрессии (bn ) известно, что b6 – b4 = 72, а b1 – b3 = 9.
a) Найдите первый член и знаменатель этой прогрессии.
b) Найдите сумму первых восьми членов геометрической прогрессии.
|
Решение:
|
(вn)- геометрическая прогрессия
в6 – в4 =72
в1 – в3 =9
Найти:в1; q; S8.
a)
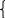 в6 – в4 =72 в6 – в4 =72
в1 – в3 =9
вn= в1 qn-1
в6= в1 q5
в4 = в1 q3
в3 = в1 q2
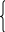 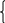 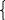 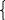 в1 q5- в1q3=72 в1 q3 ( q2 -1)=72 в1 q3 ( q2 -1)=72 в1 q3 (- в1 q5- в1q3=72 в1 q3 ( q2 -1)=72 в1 q3 ( q2 -1)=72 в1 q3 (- 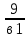 ) =72 ) =72
в1 - в1q2=9 , в1 (1 - q2)=9, (q2-1)= - 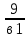 , (q2-1)= - , (q2-1)= - 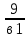 , ,
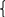 q = -2 q = -2
в1 =-3
b)
Sn.=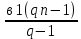 S8=.= S8=.=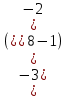 = =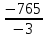 =255 =255
|
Ответ:
|
q = -2, в1 =-3 , S8 =255
|
Методические рекомендации по использованию на уроке:
|
|
3.задание
Тема:
|
Квадратичная функция и её свойства. Решение примеров
|
Цель обучения:
|
8.4.1.4 - находить значения функции по заданным значениям аргумента и находить значение аргумента по заданным значениям функции.
|
Условие задачи:
|
Мяч брошен вертикально вверх с начальной скоростью 24 м/с. Зависимость расстояния h (в метрах) от мяча до земли от времени полета выражается формулой 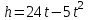 . .
1) Какой наибольшей высоты достигнет мяч?
2) Через сколько секунд после броска мяч упадет на землю?
|
Решение:
|
1) 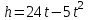 . .
х(t0)= - 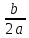 =- =- 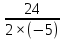 =-2,4(с) =-2,4(с)
h =24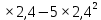 =28,8(м) =28,8(м)
2)24t- 5t2 =0
t(24 – 5t) = 0
t =0 24- 5t =0
не уд. условию задачи -5t=-24
t = 4,8
|
Ответ:
|
1)28,8 м. 2) 4,8 с.
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для закрепления темы при работе в группах. При повторении формул для нахождения вершины паработы кадратичной функции. Как самостоятельное задание при повторении.
|
4.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
8.4.2.3 использовать квадратичную функцию для решения прикладных задач
|
Условие задачи:
|
Задача.
Каковы должны быть стороны прямоугольного участка, периметр которого 120м., чтобы площадь этого участка была наибольшей?
|
Решение:
|
Пусть стороны участка a и b, тогда 2a+2b=120, значит a+b =60; b=60-а.
Площадь прямоугольника S= ab т.е. f(a)= a(60-а)= 60a – a2.
Нужно найти значение a, при котором функция принимает наибольшее значение, это парабола, которая имеет max в вершине;
a=30м., b= 30м.
|
Ответ:
|
30 м и 30м.
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
5.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Задача.
Человек заболевший гриппом, может заразить четырех человек в день.
Через сколько дней заболеет все население поселка в количестве 341 человек?
|
Решение:
|
Рассмотрим геометрическую прогрессию, где b1=1, q=4 и Sn=341. Найдем n.
В формулу Sn = 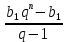 подставим: подставим:
341 =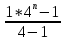
1023 = 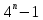
1024=4n
45=4n
n=5
|
Ответ:
|
Через 5 дней.
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
6.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Задача.
Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
|
Решение:
|
Рассмотрим арифметическую прогрессию у которой: х1=15, d=10, хn=105 мин.
хn= х1+ d(n - 1).
105= 15 + 10(n – 1)
105= 15 + 10n – 10.
10n = 100.
n =10, значит через 10 дней продолжительность воздушной ванны достигнет 1ч45мин.
|
Ответ:
|
10дней
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала
|
7.задание
Тема:
|
Арифметическая прогрессия
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Дамиру надо решить 420 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Дамир решил 13 задач. Определите, сколько задач Диас решил в последний день, если со всеми задачами он справился за 12 дней.
|
Решение:
|
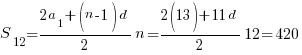
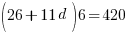
Находим 12 член прогрессии:
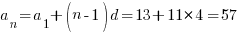
|
Ответ:
|
57
|
Методические рекомендации по использованию на уроке:
|
На этапе закрепления темы
|
8.задание
Тема:
|
Арифметическая прогрессия
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
|
Решение:
|
Используем формулу суммы арифметической прогрессии:
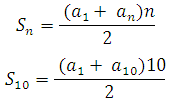 Подставим данные: Подставим данные: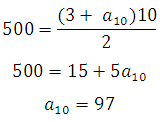
В последний день рабочие проложили 97 метров тоннеля.
|
Ответ:
|
97
|
Методические рекомендации по использованию на уроке:
|
На этапе закрепления темы
|
9.задание
Тема:
|
Арифметическая прогрессия
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Два тела, находясь на расстояни153 м друг от друга, начали двигаться одновременно навстречу друг другу. Первое тело движется со скоростью 10 м/с, второе в первую секунду прошло 3 м, а в каждую последующую - на 5 м больше, чем в предыдущую. Через сколько секунд тела встретятся?
|
Решение:
|
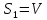 ∙ ∙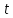 . .
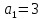 , d = 5, , d = 5,
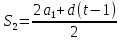 ∙ ∙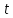 . . 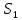 + +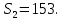
необходимо найти t.
Из условия задачи получаем уравнение: 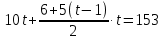
5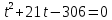
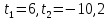 . .
Второй корень не удовлетворяет условию 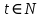 . .
|
Ответ:
|
Тела встретятся через 5 секунд.
|
Методические рекомендации по использованию на уроке:
|
На этапе закрепления темы
|
10.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
Марат коллекционирует монеты с разных стран мира. Каждый год у него появляется по 7 новых монет. Сколько монет было у Марата изначально, если через 10 лет у него стало 72 монеты?
|
Решение:
|
Решим задачу используя формулы арифметической прогрессии.
а1=Х, d = 7, N=10, S=72
а10 =а1+9*7=а1+63
а10=72 (на десятый год, по условию задачи) было 72 монеты
72= а1+63
а1 = 9 (монет было в первый год)
|
Ответ:
|
9
|
Методические рекомендации по использованию на уроке:
|
Предложить учащимся на закрепление формул нахождения N-ого члена арифметической прогрессии
|
11.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
8.4.2.3 использовать квадратичную функцию для решения прикладных задач
|
Условие задачи:
|
Камень брошен вертикально вверх. Пока
камень не упал, высота, на которой он находится,
описывается формулой h(t) = – 5t2 + 39t, где h — высота в
метрах, t — время в секундах, прошедшее с момента
броска. Найдите, сколько секунд камень находился на
высоте не менее 28 м.
|
Решение:
|
Решим неравенство: – 5t2 + 39t ≥ 28,
5t2 + 39t – 28 ≤ 0, D = 961, t1 = 0,8, t2 = 7.
На высоте не менее 28 метров, камень
находился 7 – 0,8 = 6,2 секунды.
О т в е т: 6,2 с.
|
Ответ:
|
6,2
|
Методические рекомендации по использованию на уроке:
|
Задачу можно предложить в качестве самостоятельной работы
Если ученики не будут справляться, можно предложить по шаговую инструкцию
|
12.задание
Тема:
|
Решение текстовых задач
|
Цель обучения:
|
9.4.2.2 решать текстовые задачи, связанные с геометрической и арифметической прогрессиями
|
Условие задачи:
|
В первом ряду кинотеатра 21 кресло. В каждом последующем ряду на 2 кресла больше, чем в предыдущем. Сколько кресел в 40 ряду?
|
Решение:
|
Решим задачу используя формулы арифметической прогрессии
а1= 21, d=2, n=40
найти а40 =?
а40=21+39*2=99
|
Ответ:
|
99
|
Методические рекомендации по использованию на уроке:
|
Предложить учащимся на закрепление формул нахождения N-ого члена арифметической прогрессии
| |
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
 45=1077 тыс.(жителей) население в 2020году
45=1077 тыс.(жителей) население в 2020году в6 – в4 =72
в6 – в4 =72
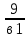 ) =72
) =72 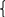 q = -2
q = -2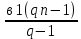 S8=.=
S8=.=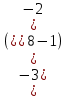 =
=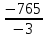 =255
=255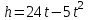 .
.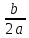 =-
=- 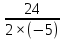 =-2,4(с)
=-2,4(с)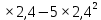 =28,8(м)
=28,8(м)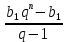 подставим:
подставим: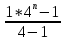
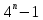
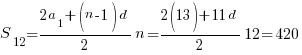
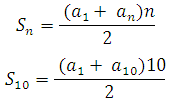 Подставим данные:
Подставим данные: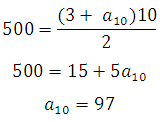
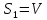 ∙
∙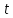 .
. 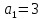 , d = 5,
, d = 5, 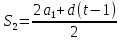 ∙
∙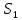 +
+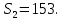
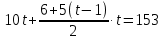
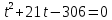
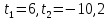 .
.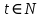 .
.