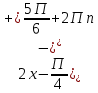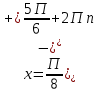Методы решения уравнений и неравенств в старшей школе
1.задание
Тема:
|
Решение иррациональных неравенств методом возведения в степень
|
Цель обучения:
|
11.2.2.5 - уметь решать иррациональные неравенства
|
Условие задачи:
|
Решить иррациональное неравенство.
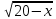 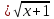
|
Решение:
|
1) Найдем ОДЗ.
x + 1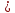 0 и 20 – x 0 и 20 – x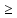 0; 0;
-1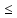 x x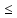 20, следовательно, ОДЗ : [-1; 20] (1) 20, следовательно, ОДЗ : [-1; 20] (1)
Возведем обе части неравенства в квадрат. 20 - x > x + 1;
2x < 19; x < 9,5 , следовательно решение этого неравенства :
(-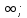 9,5) (2). 9,5) (2).
3) Найдем пресечение множеств (1) и (2), это будет множество
[-1; 9,5).
|
Ответ:
|
[-1; 9,5).
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при формативном оценивании работы учащихся в группе на закрепление.
|
2.задание
Тема:
|
Решения тригонометрических уравнений способом разложения на множители
|
Цель обучения:
|
10.2.3.9 - уметь решать тригонометрические уравнения с помощью разложения на множители
|
Условие задачи:
|
Решите уравнение
2sinx⋅sin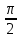 ⋅sin ⋅sin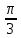 +sin2x=0 +sin2x=0
|
Решение:
|
sin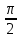 =1 и sin =1 и sin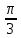 = = 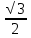 . .
По формуле синуса двойного угла sin2x=2sinxcosx,
Следовательно
2sinx⋅1⋅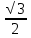 +2sinxcosx =0 +2sinxcosx =0
sinx(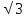 +2cosx)=0 +2cosx)=0
sinx=0 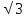 +2cosx=0 +2cosx=0
x=πn, 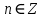 cosx= - cosx= -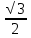
x=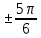 +2πm, m +2πm, m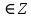
|
Ответ:
|
x=πn, 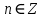
x=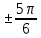 +2πm, m +2πm, m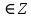
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при закреплении темы решение тригонометрических уравнений при групповой работе или индивидуальной.
|
3.задание
Тема:
|
Решение уравнений высших степеней методом введения новой переменной и замены переменной.
|
Цель обучения:
|
10.2.2.2 - применять метод введения новой переменной при решении уравнений высших степеней;
|
Условие задачи:
|
Решить уравнение: (2x−21)2−5(2x−21)+4=0.
|
Решение:
|
Обозначаем 2x−21=y. Получается простое квадратное уравнение:
у2−5y+4=0 по теореме Виета; y1=4, y2=1.
Возвращаемся к обозначенному:
1) 2x−21=4;
2x=25;
х1=12,5
|
2) 2x−21=1;
2x=22;
х2=11
|
|
Ответ:
|
х1=12,5; x2=11
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при закреплении темы при формативном оценивании учащихся.
|
4.задание
Тема:
|
Обобщенная теорема Виета для многочлена третьего порядка .
|
Цель обучения:
|
10.2.1.12 - знать обобщенную теорему Виета и применять ее к многочленам третьего порядка
|
Условие задачи:
|
Составить кубическое уравнение, корнями которого являются числа -5;3;4.
|
Решение:
|
Пусть х1 = 5; х2 = 4; х3 = -3, тогда по теореме Виета
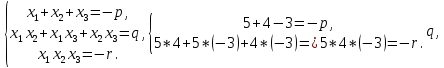
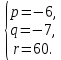
Составим приведенное кубическое уравнение вида х3 + 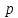 х2 + х2 + 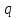 х + х + 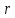 =0, корнями которого являются числа 5;4; -3. Получим х3 -6х2 -7х + =0, корнями которого являются числа 5;4; -3. Получим х3 -6х2 -7х + 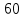 =0 =0
|
Ответ:
|
х3 -6х2 -7х + 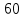 =0 =0
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
5.задание
Тема:
|
Иррациональные неравенства
|
Цель обучения:
|
11.2.2.5 - уметь решать иррациональные неравенства
|
Условие задачи:
|
Решить неравенство: (х2 -7х +6)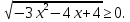
|
Решение:
|
Так как (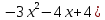 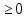 при всех допустимыхзначениях х. Значит данное неравенство равносильно системе при всех допустимыхзначениях х. Значит данное неравенство равносильно системе
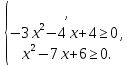
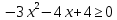 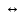 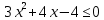 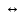 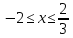
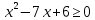 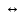 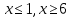
Решение системы: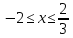
|
Ответ:
|
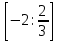
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
6.задание
Тема:
|
Логарифмические уравнения и их системы
|
Цель обучения:
|
11.2.2.8 - знать и применять методы решения логарифмических уравнений
|
Условие задачи:
|
Решить уравнение: 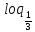 (2x -1) = log3 (2x -1) = log3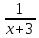 . .
|
Решение:
|
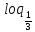 (2x -1) = log3 (2x -1) = log3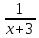 . .
Преобразуем правую часть уравнения: 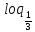 (2x -1) = - (2x -1) = - 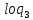 (2x -1) = (2x -1) =
= 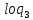 (2x -1)-1 = log3 (2x -1)-1 = log3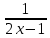 . .
Получили: log3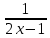 = log3 = log3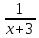 . .
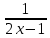 = = 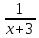
х+3 =2х -1
-х = -4
х =4.
Сделаем проверку: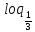 (8 -1) =: (8 -1) =: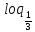 (7) = log3 (7) = log3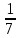
log3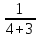 .= = log3 .= = log3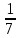
Верно, значит х =4 является корнем уравнения.
|
Ответ:
|
х = 4.
|
Методические рекомендации по использованию на уроке:
|
При изучении материала
|
7.задание
Тема:
|
Тригонометрические функции
|
Цель обучения:
|
10.2.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики
|
Условие задачи:
|
Найдите множество значений функции y x 3sin 5x - 0,1.
|
Решение:
|
Область значений функции y sin 5x , как и функции y sin x равна 1;1 . Так как при умножении на -3 происходит растяжение в 3 раза вдоль Оу графика функции y sin 5x и симметричное отображение графика функции y 3sin 5x относительно оси абсцисс, область значений функции y 3sin5x - отрезок 3;3 . А после сдвига вдоль Оу вниз на 0,1 графика последней функции, получаем окончательный ответ 3,1;2,9.
|
Ответ:
|
3,1;2,9.
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
8.задание
Тема:
|
Тригонометрические функции
|
Цель обучения:
|
10.2.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики
|
Условие задачи:
|
Используя четностью/нечетность тригонометрических функций, исследовать на четностью/нечетность функцию 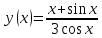
|
Решение:
|
Поменяем знак аргумента, получим,
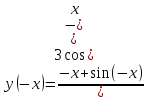
следовательно функция нечетная.
|
Ответ:
|
функция нечетная.
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
9.задание
Тема:
|
Тригонометрические уравнения
|
Цель обучения:
|
10.2.3.11 - уметь решать тригонометрические уравнения с использованием тригонометрических формул
|
Условие задачи:
|
Решить уравнение 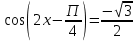
|
Решение:
|
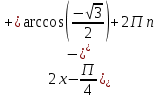
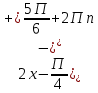
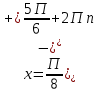
|
Ответ:
|
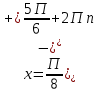
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
10.задание
Тема:
|
Иррациональные неравенства
|
Цель обучения:
|
11.2.2.5 - уметь решать иррациональные неравенства
|
Условие задачи:
|
|
Решение:
|
Выполним равносильные в ОДЗ преобразования :.
Не случайно сделано последнее преобразование. Важно знать, чему конкретно равняется функция g (x) = 2x – 8. Часто ошибкой является считать, что g (x) = 2x + 8.
ОДЗ данного неравенства: то есть Перейдём к равносильной системе.
С учётом ОДЗ сразу получаем:
Ответ.
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
11. задание
Тема:
|
Иррациональные неравенства
|
Цель обучения:
|
11.2.2.5 - уметь решать иррациональные неравенства
|
Условие задачи:
|
|
Решение:
|
Неравенство равносильно системе:
Ответ.
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
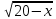
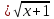
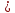 0 и 20 – x
0 и 20 – x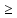 0;
0;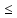 x
x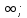 9,5) (2).
9,5) (2).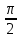
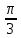
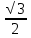 .
. 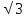
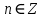
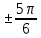 +2πm
+2πm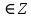
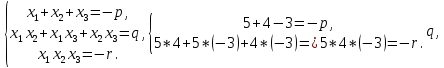
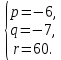
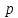 х2 +
х2 + 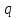 х +
х + 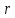 =0, корнями которого являются числа 5;4; -3. Получим х3 -6х2 -7х +
=0, корнями которого являются числа 5;4; -3. Получим х3 -6х2 -7х + 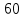 =0
=0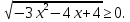
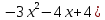
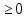 при всех допустимыхзначениях х. Значит данное неравенство равносильно системе
при всех допустимыхзначениях х. Значит данное неравенство равносильно системе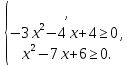
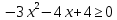
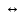
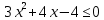
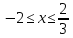
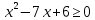
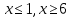
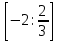
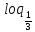 (2x -1) = log3
(2x -1) = log3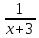 .
.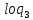 (2x -1) =
(2x -1) = 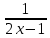 .
.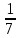
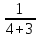 .= = log3
.= = log3