|
|
задания по МОДО. ИтоговаяРабота - 4 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Прикладные задачи на математическое моделирование и анализ в старших классах
1.задание
Тема:
|
Предел функции
|
Цель обучения:
|
10.4.1.8 - знать определение предела функции в точке и вычислять его
|
Условие задачи:
|
Найти предел функции в точке
|
Решение:
|
|
Ответ:
|
-3
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
2.задание
Тема:
|
Предел функции
|
Цель обучения:
|
10.4.1.9 - знать определение предела функции на бесконечности и вычислять его;
|
Условие задачи:
|
Вычислить предел
|
Решение:
|
Для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим числитель и знаменатель на
|
Ответ:
|
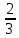
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
3.задание
Тема:
|
Предел функции
|
Цель обучения:
|
10.4.1.9 - знать определение предела функции на бесконечности и вычислять его;
|
Условие задачи:
|
Найти предел
|
Решение:
|
Разделим числитель и знаменатель на
|
Ответ:
|
0
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
4.задание
Тема:
|
Определение наибольшего и наименьшего значения функции на отрезке
|
Цель обучения:
|
10.4.1.34 - находить наибольшее и наименьшее значения функции на отрезке;
|
Условие задачи:
|
Найдите наименьшее значение функции у=х-4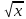 на промежутке [1;9] на промежутке [1;9]
|
Решение:
|
D(f)=[0; +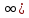
y1= 1- 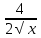
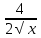 =0; 1- =0; 1-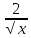 =0 =0
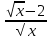 =0 =0
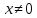 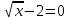
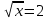
x=4 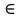 [1;9] [1;9]
y(4)=4-4*2=-4
y(1)=1-4=-3
y(9)=9-4*3=-3
yнаим. =-4
|
Ответ:
|
-4
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при проведении формативного оценивания учащихся или при закреплении темы урока в групповой работе.
|
5.задание
Тема:
|
Площадь плоской фигуры, ограниченной заданными линиями.
|
Цель обучения:
|
11.4.1.8 - вычислять площадь плоской фигуры, ограниченной заданными линиями;
|
Условие задачи:
|
Вычислить площадь фигуры, ограниченной линиями:
у=х2+3; у=0; х=-1; х=2
|
Решение:
|
2
S =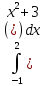 =( =(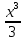 +3x) = ( +3x) = (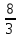 +6)- (- +6)- (-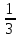 -3) =8 -3) =8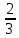 + 3 + 3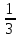 = 12 (кв.ед) = 12 (кв.ед)
-1
|
Ответ:
|
12 (кв.ед)
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при закреплении темы учащимися , в тестовых заданиях при повторении раздела, при составлении заданий для СОР.
|
6.задание
Тема:
|
Вычисление объема тела вращения с помощью определенного интеграла.
|
Цель обучения:
|
11.4.1.9 - знать и применять формулу вычисления объема тела вращения с помощью определенного интеграла;
|
Условие задачи:
|
Найдите объем тела, полученной вращением криволинейной трапеции вокруг оси ОХ, ограниченной линиями у =х2; у=0; х=0; х=2.
|
Решение:
|
V=π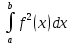
 2 2
V=π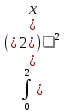 dx =π dx =π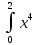 dx =π dx =π 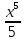 =π* =π*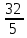 =6,4 π (куб.ед) =6,4 π (куб.ед)
0
|
Ответ:
|
6,4 π (куб.ед)
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при закреплении темы учащимися , в тестовых заданиях при повторении раздела, при составлении заданий для СОР.
|
7.задание
Тема:
|
Физический и геометрический смысл производной
|
Цель обучения:
|
10.4.2.1 - знать геометрический смысл производной
|
Условие задачи:
|
К графику функции у=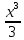 проведите касательную, так чтобы она была параллельна прямой у=4х+7. проведите касательную, так чтобы она была параллельна прямой у=4х+7.
|
Решение:
|
Если касательная параллельна прямой у=4х+7, то угловой коэффициент этой касательной k=4 и k= 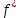 (x0). (x0).
Найдем 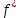 (x)= (x)= 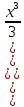 = х2, тогда = х2, тогда 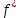 (x0)= = х02 = 4. и х0= -2, х0=2. (x0)= = х02 = 4. и х0= -2, х0=2.
То есть имеются две касательные, удовлетвторяющие условию задачи: а) составим уравнение касательной в точке х0= 2:
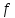 (x0) = (x0) =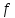 (2) = (2) = 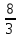 ; ;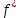 (x0) = (x0) = 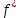 (2) = 4; у = (2) = 4; у = 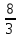 + 4(х -2) или у = 4х - + 4(х -2) или у = 4х - 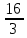 . .
в) составим уравнение касательной в точке х0= -2:
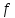 (x0) = (x0) =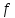 (-2) = - (-2) = - 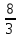 ; ;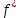 (x0) = (x0) = 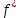 (-2) = 4; у = (-2) = 4; у = 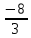 + 4(х +2) или у = 4х + + 4(х +2) или у = 4х + 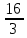 . .
|
Ответ:
|
у = 4х - 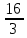 или у = 4х + или у = 4х + 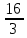 . .
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала или для ф.о.
|
8.задание
Тема:
|
Физический и геометрический смысл производной
|
Цель обучения:
|
10.4.3.1 - решать прикладные задачи, опираясь на физический смысл производной
|
Условие задачи:
|
Тело, масса которого 5 кг, движется прямолинейно по закону
S(t) = 1-t + t2 , где S- измеряется в метрах, а t в секундах. Найти кинетическую энергию тела через 10с после начала движения
|
Решение:
|
. S(t) = 1-t + t2 по условию m =5 кг, t = 10с и кинетическая энергия вычисляется по формуле Е =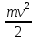 . .
Найдем v= S´( t) = (1-t + t2 )´ = -1 +2t =2 t - 1
v( t) = v( 10) = 2·10 -1 = 19(м/с)
Е = =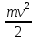 = = = =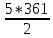 = 902,5 (Дж) = 902,5 (Дж)
|
Ответ:
|
902,5 Дж
|
Методические рекомендации по использованию на уроке:
|
При закреплении материала или для ф.о.
|
9.задание
Тема:
|
Наибольшее и наименьшие значения функции на отрезке.
|
Цель обучения:
|
10.4.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Условие задачи:
|
Марат решил сделать своей маме подарок и заказал другу Дамиру шкатулку из драгоценного металла. В мастерскую он принес кусок листа из этого металла размером 80 х 50 см. Требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и загибая оставшиеся кромки.
|
Решение:
|
   х х х х

Обозначим через х см высоту вырезаемой коробки, где 0
тогда (80 – 2х) см– длина коробки
(50 -2х) см ширина коробки.
Объем коробки:
V (х)= x (80 - 2х) (50 – 2х) = 4х³ - 260х² + 4000х.
V´(х) = 12х² - 520х + 4000
V´(х) = 0, 12х² - 520х + 4000=0
х1 = 100:3 = 33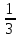 , х2= 10. , х2= 10.
х1- посторонний корень по смыслу задачи.
х2= 10 – единственное решение
 + - + -
10
При х=10, V (х)- максимальное значение.
х = 10 см– высота, 80 – 20 = 60 см– длина, 50 – 20 = 30 см– ширина.
|
Ответ:
|
Коробка имеет размеры:10х60х30 см.
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
10.задание
Тема:
|
Наибольшее и наименьшие значения функции на отрезке.
|
Цель обучения:
|
10.4.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Условие задачи:
|
Каковы размеры прямоугольника наибольшей площади, который можно вписать в полукруг радиуса R таким образом, чтобы одна сторона прямоугольника лежала на диаметре полукруга?
|
Решение:
|
Решение задачи сводится к нахождению того значения DC=x и, следовательно, CB=у=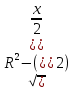 , при котором функция S(х)=ху=x , при котором функция S(х)=ху=x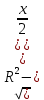 принимает свое наибольшее значение на промежутке (0; 2R). Ясно, что вместо функции S(x) целесообразно исследовать функцию f(x) = S2(x) отрезке [0; 2R]. принимает свое наибольшее значение на промежутке (0; 2R). Ясно, что вместо функции S(x) целесообразно исследовать функцию f(x) = S2(x) отрезке [0; 2R].
Ответ: 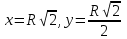 . .
|
Ответ:
|
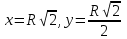
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
11.задание
Тема:
|
Наибольшее и наименьшие значения функции на отрезке.
|
Цель обучения:
|
10.4.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Условие задачи:
|
Стоимость эксплуатации катера, плывущего со скоростью 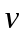 км/час, составляет 90+0,4 км/час, составляет 90+0,4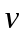 2 руб/час. С какой скоростью должен плыть катер, чтобы стоимость эксплуатации катера на 1 км пути была наименьшей? 2 руб/час. С какой скоростью должен плыть катер, чтобы стоимость эксплуатации катера на 1 км пути была наименьшей?
|
Решение:
|
По условию задачи стоимость эксплуатации катера, плывущего со скоростью 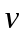 км/час, равна 90+0,4 км/час, равна 90+0,4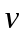 2 руб/час. Но за 1 час катер проплывает 2 руб/час. Но за 1 час катер проплывает 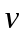 км. Значит, стоимость эксплуатации катера за 1 км пути равна км. Значит, стоимость эксплуатации катера за 1 км пути равна 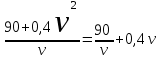 (руб/км). (руб/км).
Таким образом, требуется определить, при каком значении 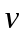 функция S( функция S(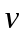 )= )=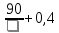 принимает свое наименьшее значение на луче (0;+ ∞). принимает свое наименьшее значение на луче (0;+ ∞).
Найдем критические точки этой функции: 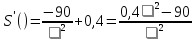 . Производная существует в каждой точке промежутка (0; + ∞). Далее S’( . Производная существует в каждой точке промежутка (0; + ∞). Далее S’(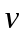 ) = 0↔ ) = 0↔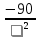 + 0,4 = 0↔ + 0,4 = 0↔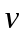 2 = 225 ↔ 2 = 225 ↔ 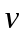 =15 или =15 или 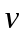 = =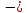 15. Из двух найденных критических точек лишь одна, а именно 15. Из двух найденных критических точек лишь одна, а именно 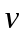 =15, принадлежит промежутку (0; + ∞). =15, принадлежит промежутку (0; + ∞).
Так как 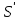 ( (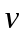 ) < 0 на промежутке (0; 15) и ) < 0 на промежутке (0; 15) и 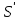 ( (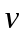 ) > 0 на промежутке (15; + ∞), то ) > 0 на промежутке (15; + ∞), то 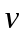 =15 является точкой минимума функции S( =15 является точкой минимума функции S(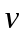 ). Наконец, так как функция S( ). Наконец, так как функция S(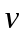 ) убывает на (0; 15) и возрастает на (15; + ∞), то эта функция достигает своего наименьшего значения на промежутке (0; + ∞) в точке ) убывает на (0; 15) и возрастает на (15; + ∞), то эта функция достигает своего наименьшего значения на промежутке (0; + ∞) в точке 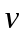 =15. =15.
|
Ответ:
|
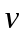 =15 км/час. =15 км/час.
|
Методические рекомендации по использованию на уроке:
|
При изучении материала.
|
12.задание
Тема:
|
Наибольшее и наименьшие значения функции на отрезке.
|
Цель обучения:
|
10.4.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Условие задачи:
|
Число 26 представить в виде суммы трех положительных слагаемых, сумма квадратов которых наименьшая, если известно, что второе слагаемое втрое больше первого.
|
Решение:
|
Обозначим неизвестные слагаемые через x, y, z. По условию задачи введенные неизвестные удовлетворяют системе уравнений: 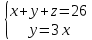 . Выразим неизвестное y и z через x. Получим y=3x, z=26-4x. . Выразим неизвестное y и z через x. Получим y=3x, z=26-4x.
Таким образом, задача сводится к исследованию функции
S(x)= x2+9x2+(26-4x)2, или S(x)=26x2 - 208x+676.
Промежуток изменения аргумента в данном случае определяем из условия положительности всех слагаемых:
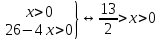 . .
Итак, решение задачи сведено к нахождению наименьшего значения функции S(x) на (0;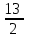 ). Так как функция S(x) непрерывна и на отрезке [0; ). Так как функция S(x) непрерывна и на отрезке [0;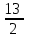 ], то рассмотрим сначала ее на этом отрезке. Имеем: S'(x)=52x–208; S'(x)=0 ], то рассмотрим сначала ее на этом отрезке. Имеем: S'(x)=52x–208; S'(x)=0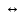 52x–208=0 52x–208=0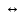 x=4. Так что единственной критической точкой функции S(x) является x=4 x=4. Так что единственной критической точкой функции S(x) является x=4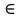 (0; (0;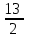 ). Осталось сравнить числа S(0)=676, S(4)=260 иS( ). Осталось сравнить числа S(0)=676, S(4)=260 иS(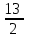 )=422,5. )=422,5.
Таким образом, наименьшее значение на отрезке [0; 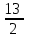 ] функция S(x) достигает во внутренней точке x=4 этого отрезка. Значит, число S(4)=260 является наименьшим значением функции S(x) и на промежутке (0; ] функция S(x) достигает во внутренней точке x=4 этого отрезка. Значит, число S(4)=260 является наименьшим значением функции S(x) и на промежутке (0; 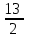 ). ).
З а м е ч а н и е. Число S(0)=676 является наибольшим значением функции S(x) на отрезке [0; 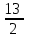 ]. Однако, как легко видеть, функция S(x) на промежутке (0; ]. Однако, как легко видеть, функция S(x) на промежутке (0; 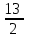 ) не достигает своего наибольшего значения. ) не достигает своего наибольшего значения.
Ответ: 26=4+12+10.
|
Ответ:
|
26=4+12+10.
|
Методические рекомендации по использованию на уроке:
|
При изучении темы
|
Использованная литература
|
справочник с решениями задач, автор А. Ж. Жумадилова,
сборник задач Рыжкова И.Г.
задачи с практическим содержанием, как средство формирования геометрических представлений учащихся И.М.Смирнова, В.А.Смирнов
комплексные числа И.В.Деменева
комплексные числа В.Н. Акимов, И.Н. Коновалова
тригонометрические уравнения Ю.И. Галанов, Е.Н. Некряч, В.И. Рожкова
Дорофеев Г., Потапов М., Розов Н. Математика для поступающих в вузы. М.: Дрофа, 2002
|
|
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
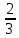
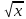 на промежутке [1;9]
на промежутке [1;9]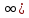
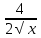
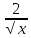 =0
=0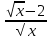 =0
=0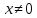
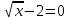
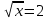
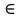 [1;9]
[1;9]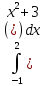 =(
=(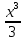 +3x) = (
+3x) = (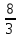 +6)- (-
+6)- (-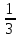 -3) =8
-3) =8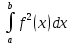
 2
2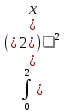 dx =π
dx =π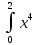 dx =π
dx =π 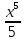 =π*
=π*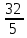 =6,4 π (куб.ед)
=6,4 π (куб.ед) 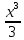 проведите касательную, так чтобы она была параллельна прямой у=4х+7.
проведите касательную, так чтобы она была параллельна прямой у=4х+7.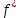 (x0).
(x0). 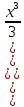 = х2, тогда
= х2, тогда 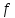 (x0) =
(x0) =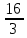 .
.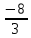 + 4(х +2) или у = 4х +
+ 4(х +2) или у = 4х + 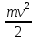 .
. 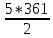 = 902,5 (Дж)
= 902,5 (Дж)


 + -
+ -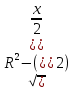 , при котором функция S(х)=ху=x
, при котором функция S(х)=ху=x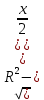 принимает свое наибольшее значение на промежутке (0; 2R). Ясно, что вместо функции S(x) целесообразно исследовать функцию f(x) = S2(x) отрезке [0; 2R].
принимает свое наибольшее значение на промежутке (0; 2R). Ясно, что вместо функции S(x) целесообразно исследовать функцию f(x) = S2(x) отрезке [0; 2R].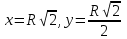 .
.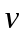 км/час, составляет 90+0,4
км/час, составляет 90+0,4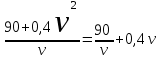 (руб/км).
(руб/км).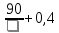 принимает свое наименьшее значение на луче (0;+ ∞).
принимает свое наименьшее значение на луче (0;+ ∞).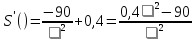 . Производная существует в каждой точке промежутка (0; + ∞). Далее S’(
. Производная существует в каждой точке промежутка (0; + ∞). Далее S’(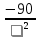 + 0,4 = 0↔
+ 0,4 = 0↔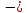 15. Из двух
15. Из двух 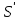 (
(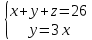 . Выразим неизвестное y и z через x. Получим y=3x, z=26-4x.
. Выразим неизвестное y и z через x. Получим y=3x, z=26-4x. 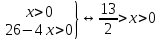 .
.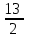 ). Так как функция S(x) непрерывна и на отрезке [0;
). Так как функция S(x) непрерывна и на отрезке [0;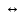 52x–208=0
52x–208=0