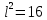Навигация по странице:Дано
|
задания по МОДО. ИтоговаяРабота - 4 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
9.задание
Тема:
|
Теорема синусов
|
Цель обучения:
|
9.1.3.7 знать и применять теорему синусов;
|
Условие задачи:
|
Для определения ширины непроходимого болота с вертолета, находящегося на высоте h, измерили углы α и β. Найдите ширину болота
|
Решение:
|
Дано:
<САD = α; <СВА = β; СD = h
Найти: АВ.
Решение:
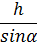 Из прямоугольного ∆АCD находим: Из прямоугольного ∆АCD находим:
АС =
2.Из ∆АВС теореме о внешнем угле треугольника
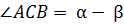
3.По теореме синусов имеем:
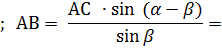 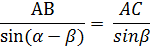 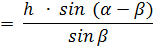
 С С
D A B
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Предложить работу в группах
|
10.задание
Тема:
|
Теорема синусов
|
Цель обучения:
|
9.1.3.7 знать и применять теорему синусов;
|
Условие задачи:
|
В треугольнике АВС сторона АВ = 8 см, <С=600, <В = 45°. Найдите сторону АС.
|
Решение:
|
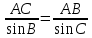
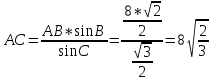
|
Ответ:
|
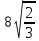
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
11.задание
Тема:
|
Векторы
|
Цель обучения:
|
9.1.4.3 применять условие коллинеарности векторов
|
Условие задачи:
|
Даны точки А(-2; 3; 1), В(-2; 1; 2) и С(0; 3; 4). Проверьте перпендикулярность векторов АВ и АС.
даны точки A(2, 4) B(6,-4) C(-8,-1) докажите что векторы ab и ac перпендикулярны! заранее большое вам спасибо
|
Решение:
|
АВ( 0; -2; 1 ), АС( 2; 0; 3).
Скалярное произведение этих векторов равно
0*2+(-2)*0+1*3 =3.
Если скалярное произведение равно 0, то векторы перпендикулярны.
Данные векторы не перпендикулярны.
|
Ответ:
|
Данные векторы не перпендикулярны.
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
12.задание
Тема:
|
Векторы
|
Цель обучения:
|
9.1.4.4 раскладывать вектор по двум неколлинеарным векторам
|
Условие задачи:
|
Пусть M — середина отрезка AB, O — произвольная точка. Докажите, что OM=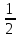 (OA+OB) (OA+OB)
(везде сверху букв знак вектора)
|
Решение:
|
OM=OA+AM=OB+BM
Сложив почленно равенства
OM=OA+AM
OM=OB+BM
получим:
2 OM=(OA+OB)+(AM+BM)=OA+OB+0=OA+OB
Следовательно,
OM=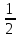 (OA+OB) (OA+OB)
|
Ответ:
|
Доказано, что OM=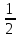 (OA+OB) (OA+OB)
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
Решение задач стереометрии
1.задание
Тема:
|
Сечения многогранников плоскостями
|
Цель обучения:
|
11.1.4.1 Уметь строить сечения многогранника плоскостями
|
Условие задачи:
|
Дан куб ABCDA1B1C1D1 с ребром a. Постройте сечение куба плоскостью, проходящей через середины рёбер AB, BB1 и B1C1.
|
Решение:
|
Пусть M, L, N - заданные точки. Строим PR || LN и KR || ML . Соединяем N c K и M c P . Прямые NK и MP также должны быть параллельны. Легко доказать, что все перечисленные условия параллельности будут выполнены одновременно, если изначально точку R расположить в середине ребра DD1.
|
Ответ:
|
Искомое сечение МLNKRP
|
Методические рекомендации по использованию на уроке:
|
Предложить учащимся для самостоятельной работы
|
2.задание
Тема:
|
Нахождение угла в пространстве
|
Цель обучения:
|
11.2.4.1.Уметь находить угол между прямыми и угол между прямой и плоскостью
|
Условие задачи:
|
|
Решение:
|
|
Ответ:
|
60
|
Методические рекомендации по использованию на уроке:
|
Предложить учащимся для работы в группе
|
3.задание
Тема:
|
Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах
|
Цель обучения:
|
10.2.8 - знать определение перпендикуляра, наклонной и проекции наклонной в пространстве;
10.3.1 - знать теорему о трех перпендикулярах и применять её при решении задач;
10.2.9 - знать определение угла между двумя прямыми в пространстве;
10.2.10 - уметь изображать угол между скрещивающимися прямыми и их общий перпендикуляр;
|
Условие задачи:
|
Пусть SABC – правильная треугольная пирамида с вершиной S. Найдите угол между AS и BC. Ответ дайте в градусах.
|
Решение:
|
|
Ответ:
|
90
|
Методические рекомендации по использованию на уроке:
|
Предложить учащимся для самостоятельной работы
|
4.задание
Тема:
|
Площадь полной поверхности призмы
|
Цель обучения:
|
11.3.1 - выводить формулы площади боковой и полной поверхности призмы и применять их при решении задач
|
Условие задачи:
|
Стороны основания прямой треугольной призмы равны 12 см, 13 см и 5 см, а боковое ребро равно большей высоте основания. Найдите площадь полной поверхности призмы.
|
Решение:
|
Sп.пов. =Sбок+2 Sосн.=Росн.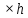 +2Sосн. +2Sосн.
Росн.=12+13+5=30(см)
Sосн.=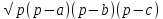 = =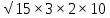 = =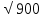 =30(см2) =30(см2)
h =2S :с =2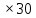 :5=12(см) :5=12(см)
Sп.пов.=30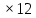 +2 +2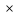 30=420(см2) 30=420(см2)
|
Ответ:
|
420 см2
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для работы в группе при решении задач на повторение формул площади треугольника, закреплении фомулы площади прямой призмы.
|
5.задание
Тема:
|
Площадь боковой и полной поверхности усеченной пирамиды
|
Цель обучения:
|
11.3.2 - выводить формулы площади боковой и полной поверхности пирамиды (усеченной пирамиды) и применять их при решении задач;
|
Условие задачи:
|
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
|
Решение:
|
Объем усеченной пирамиды может быть найден по формуле
V = 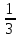 H · (S1 + S2 + √(S1 · S2)), H · (S1 + S2 + √(S1 · S2)),
где S1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p1 = 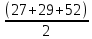 = 54. = 54.
S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
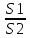 = ( = ( 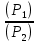 )2= )2= 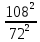 = = 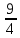 . .
Отсюда S2 = 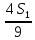 = = 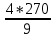 = 120. = 120.
Итак, V = 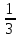 · 10(270 + 120 + √(270 · 120)) = 1900. · 10(270 + 120 + √(270 · 120)) = 1900.
|
Ответ:
|
1900 куб.ед.
|
Методические рекомендации по использованию на уроке:
|
Можно использовать на закрепление формулы объема с повторением понятия подобия треугольников и нахождения площади треугольника.
|
6.задание
Тема:
|
Объем шара и его частей
|
Цель обучения:
|
11.3.16 — знать формулы нахождения объема шара и его частей и применять их при решении зада
|
Условие задачи:
|
Объем шара равен 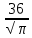 . Чему будет равна площадь поверхности шара, если его радиус увеличить на . Чему будет равна площадь поверхности шара, если его радиус увеличить на 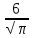 ? ?
|
Решение:
|
Vшара= 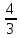 πR3= πR3= 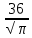 ⇒ R= ⇒ R= 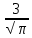 . .
Радиус нового шара равен:
Rнов. = R+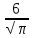 = = 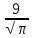 . .
Тогда найдем площадь поверхности:
Sпов.=4πR2нов. =4π(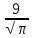 )2=4π )2=4π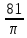 = 324. = 324.
|
Ответ:
|
324
|
Методические рекомендации по использованию на уроке:
|
Можно использовать в групповой работе на применение формулы объема шара и площади поверхности сферы. При проверки умений применять формулы в СОРе.
|
7.задание
Тема:
|
Многоранники
|
Цель обучения:
|
11.3.3 - решать задачи на нахождение элементов многогранников
|
Условие задачи:
|
В основании прямоугольного параллелепипеда лежит квадрат со стороной 4, высота параллелепипеда равна 2. Найти диагонали прямоугольного параллелепипеда.(6)
|
Решение:
|
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
d² = a² + b² + c²
Так как основание квадрат то
d²=4²+4²+2²=36 d=6
|
Ответ:
|
d=6
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
8.задание
Тема:
|
Многоранники
|
Цель обучения:
|
11.3.3 - решать задачи на нахождение элементов многогранников
|
Условие задачи:
|
В прямой пятиугольной призме все ребра равны. Площадь боковой поверхности равна 80 см2. Найдите высоту призмы.
|
Решение:
|
S=P*l
P*l=80
5*l*l=80
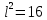
l=4
|
Ответ:
|
4 cм
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
| |
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
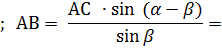
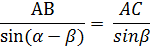
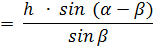
 С
С 
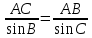
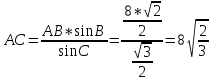
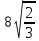
 (
(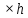 +2Sосн.
+2Sосн.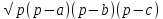 =
=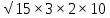 =
=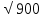 =30(см2)
=30(см2) :5=12(см)
:5=12(см)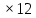 +2
+2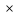 30=420(см2)
30=420(см2)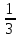 H · (S
H · (S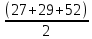 = 54.
= 54.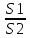 = (
= ( 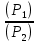 )2=
)2= 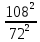 =
= 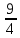 .
. 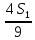 =
= 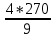 = 120.
= 120.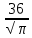 . Чему
. Чему 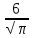 ?
?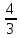
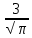 .
.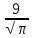 .
. 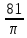 = 324.
= 324.