|
|
Методические указания и индивидуальные задания для выполнения типового расчета Хабаровск Издательство двгупс 2007 удк 519. 2 (075. 8)
Вариант № 27
При наборе телефонного номера абонент забыл две последние цифры и выбрал их наудачу, помня только, что эти цифры нечетные и разные. Сколькими разными способами он может сделать этот выбор?
В барабан револьвера заложены четыре боевых патрона и три пустые гильзы. Барабан прокручивается произвольно и производится два выстрела. Определить вероятность того, что: а) оба выстрела холостые;
б) один выстрел холостой.
На предприятии три телефона. Вероятности их занятости соответственно равны: 0,6; 0,4; 0,5. Какова вероятность того, что: а) хотя бы один телефон свободен, б) все телефоны свободны?
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-4;-1]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
На сборку поступили детали с трех автоматов: первый дает 15% деталей, второй – 30%, третий – 55%. Первый автомат допускает 0,1% брака, второй – 0,2% брака, третий – 0,3% брака. Найти вероятность того, что бракованная деталь изготовлена на первом автомате.
Вероятность отказа прибора за время Т равна 0,001. Найти вероятность того, что из 2000 приборов за время Т откажут 2 прибора.
Вероятность выигрыша в лотерее на 1 билет равна 0,3. Куплено
13 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,8. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9573 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,03?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 500 поступивших вызовов имеется 6 сбоев.
В партии 12 деталей, из них 3 нестандартные. Наудачу отобраны 3 детали. Составить закон распределения числа нестандартных деталей среди отобранных. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
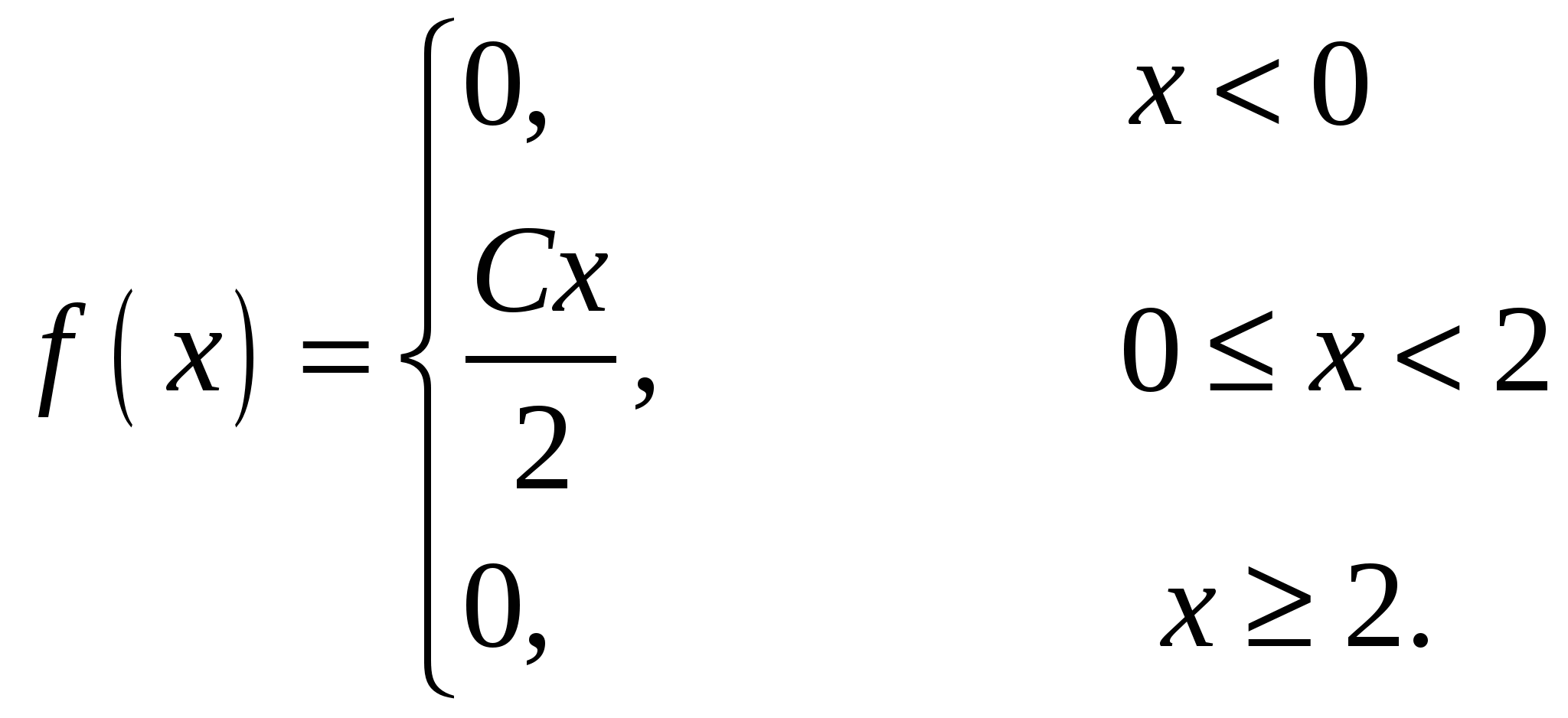
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (1/2;4/3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
10
|
15
|
20
|
24
|
|
У
|
10
|
1
|
-3
|
Р
|
0,1
|
0,7
|
0,15
|
0,05
|
|
Р
|
0,25
|
0,35
|
0,4
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0567 отклонится от своего математического ожидания менее, чем на 0,012.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
2,3
|
2,7
|
26
|
0,05
|
0,09
|
30
|
0,12
|
0,30
|
41
|
0,08
|
0,11
|
50
|
0,04
|
0,21
|
|
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.