Вариант № 25
Некто выбирает наугад 6 клеток “Спортлото” (6 из 49). В скольких случаях он правильно угадает из числа выигравших 6 номеров ровно три; ровно четыре; ровно пять; все шесть номеров?
На каждой из шести набранных карточек напечатана одна из следующих букв: А, Т, И, Р, С, О. Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной и расположенных в одну линию карточках можно будет прочесть слово «ТРОС».
Вероятность попадания в цель при каждом выстреле для трех стрелков равна 4/5, 3/4, 2/3 соответственно. При одновременном выстреле всех трех стрелков имелось одно попадание. Определить вероятность того, что в цель промахнулся третий стрелок.
Наудачу взяты 2 положительных числа Х и У, каждое их них не превышает двух. Найти вероятность того, что произведение ХУ будет не больше 2,6, а частное Х/У не больше 2.
В спецбольницу поступает в среднем 50% больных с заболеванием сердца, 30%- с заболеванием почек, 20% с заболеванием печени. Вероятность полного излечения болезни сердца равна 0,7, для болезни почек – 0,8, для болезни печени – 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что больной страдал заболеванием почек.
Принимая одинаково вероятным рождение мальчика и девочки,
найти вероятность того, что из 4000 новорожденных будет от 1950 до
2050 мальчиков.
Вероятность выигрыша в лотерее на 1 билет равна 0,7. Куплено 12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,2. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9879 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,01?
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 600 поступивших вызовов имеется 9 сбоев.
Найти закон распределения Х и математическое ожидание случайной величины, которая может принимать только два значения х1 и х2. причем х1< х2, D(Х)=7,56 и вероятность того, что случайная величина Х примет значение х2 равна 0,3.
Случайная величина Х задана плотностью распределения:
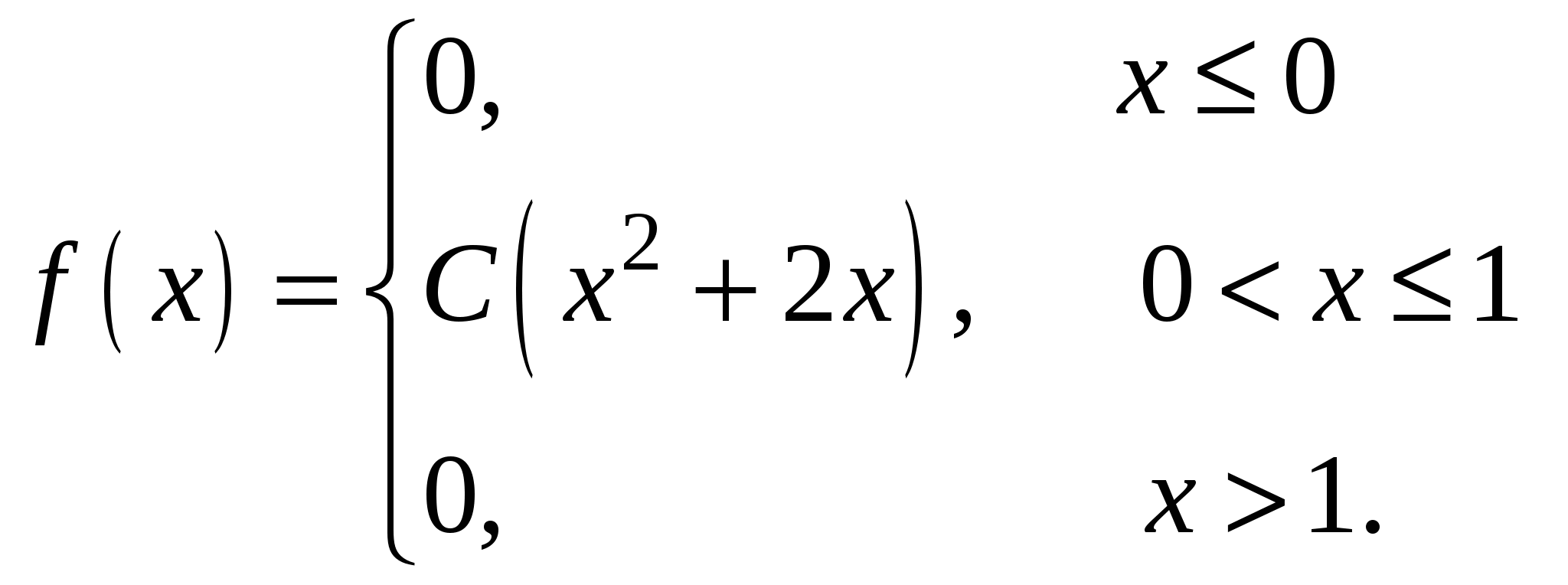
Найти параметр С, функцию распределения F(х) случайной величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (0; 0,25). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
0,3
|
0,5
|
0,7
|
0,9
|
|
У
|
1,1
|
1,3
|
1,7
|
У
|
0,4
|
0,3
|
0,2
|
0,1
|
|
Р
|
0,5
|
0,4
|
0,1
|
Укажите законы распределения случайной величины Х+У, Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0015 отклонится от математического ожидания менее, чем на 0,1.
Двумерная случайная величина (Х, У) задана таблицей. Найдите её ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
у х
|
1
|
2
|
3
|
1,1
|
0,1
|
0,06
|
0,09
|
4,8
|
0,09
|
0,04
|
0,11
|
6,7
|
0,07
|
0,09
|
0,13
|
9,7
|
0,01
|
0,04
|
0,17
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.