Вариант № 23
Лифт в пятиэтажном доме отправляется с тремя пассажирами. Сколько различных способов имеется для их выхода из лифта? В скольких случаях на каждом этаже выйдет не более одного пассажира? Пассажиры выходят на 2, 3, 4, 5 этажах.
Какова вероятность того, что четырехзначный номер случайно взятого автомобиля в большом городе а) имеет все цифры разные, б) имеет все цифры одинаковые?
Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие будет высшего сорта равна 0,8. Найти вероятность того, что из трех наугад взятых изделий только два будут высшего сорта.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает 2,5. Найти вероятность того, что произведение ХУ будет не больше 1, а частное У/Х не больше 2,5.
Некто, заблудившийся в лесу, вышел на поляну, откуда ведет пять дорог. Известно, что вероятности выхода из леса за час для различных дорог равны 0,6; 0,3; 0,2; 0,4; 0,1 соответственно. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час?
Статистикой установлено, что из каждой тысячи родившихся детей в среднем рождаются 315 девочек и 485 мальчиков. В семье пятеро детей. Найти вероятность того, что среди этих детей три девочки.
Вероятность выигрыша в лотерее на 1 билет равна 0,6. Куплено
15 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,5. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,966 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,02?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 400 поступивших вызовов имеется 9 сбоев.
В одной урне четыре шара, в другой – три шара. На каждом шаре отмечено число очков от одного до четырех для первой урны и от одного до трех – для второй. Из каждой урны наугад извлекают по одному шару. Составить закон распределения суммы очков на вынутых шарах. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
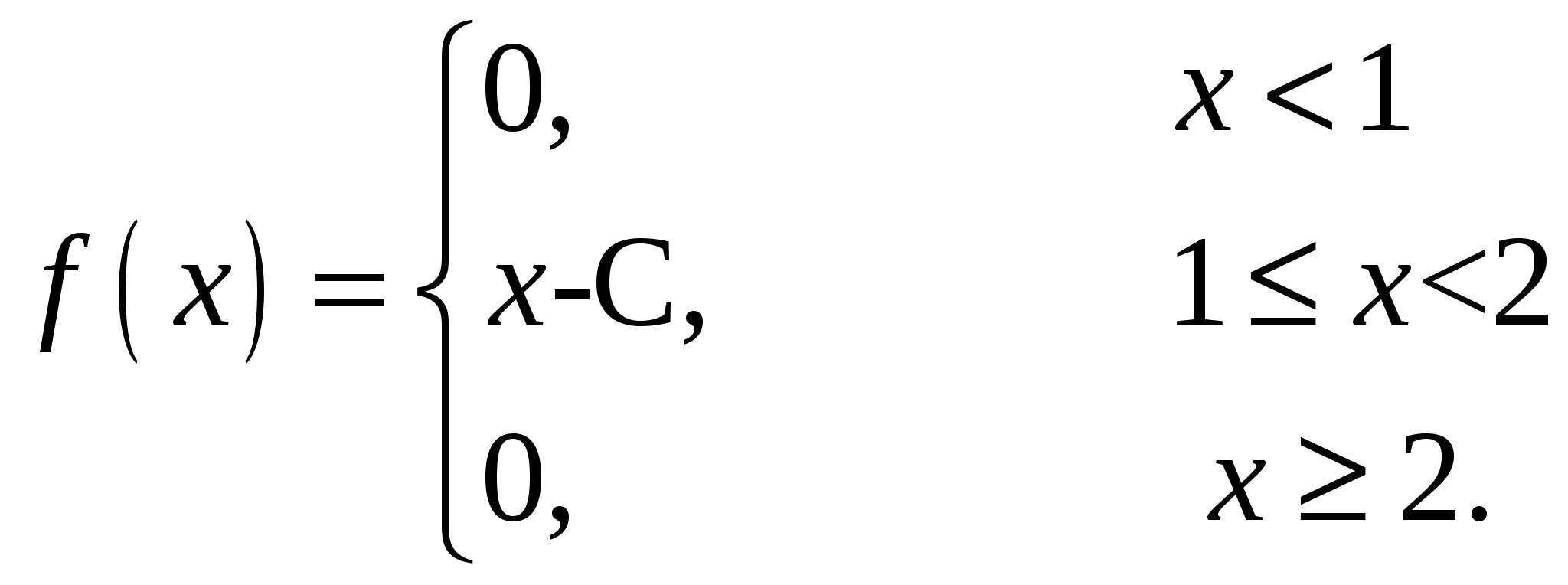
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (1,9;3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
1
|
2
|
3
|
4
|
|
У
|
2
|
4
|
6
|
Р
|
0,2
|
0,3
|
0,4
|
0,1
|
|
Р
|
0,6
|
0,2
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0121 отклонится от своего математического ожидания менее, чем на 0,33.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
1
|
0,09
|
0,04
|
0,03
|
3
|
0,08
|
0,21
|
0,04
|
8
|
0,03
|
0,15
|
0,21
|
10
|
0,01
|
0,05
|
0,06
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.