Вариант № 19
Сколько четырехзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5, если никакая цифра не повторяется более одного раза? Если повторения цифр допустимы?
В ящике находится 15 годных и 5 бракованных деталей. Найти вероятность того, что среди трех наудачу вынутых деталей нет бракованных.
Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8, из второго – 0,2, из третьего – 0,9. Найти вероятность того, что хотя бы один выстрел попадает в цель.
Наудачу взяты 2 положительных числа Х и У, каждое их них не превышает единицы. Найти вероятность того, что произведение ХУ будет не меньше 0,085, а сумма Х+У не превышает единицы.
С одного автомата на сборку поступает 20% деталей, со второго – 30%, с третьего – 50%. Первый автомат дает в среднем 0,2% брака, второй – 0,3%, третий – 0,1%. Найти вероятность того, что оказавшаяся бракованной деталь изготовлена на втором автомате.
Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отработанных деталей окажется непроверенных от 70 до 100 деталей.
Вероятность выигрыша в лотерее на 1 билет равна 0,6. Куплено
13 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,7. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,803 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 500 поступивших вызовов имеется 8 сбоев.
Из орудия ведется стрельба по цели до первого попадания, но производится не более трех выстрелов. Вероятность попадания при одном выстреле равна 0,6. Составить закон распределения числа произведенных залпов, найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана плотностью распределения:
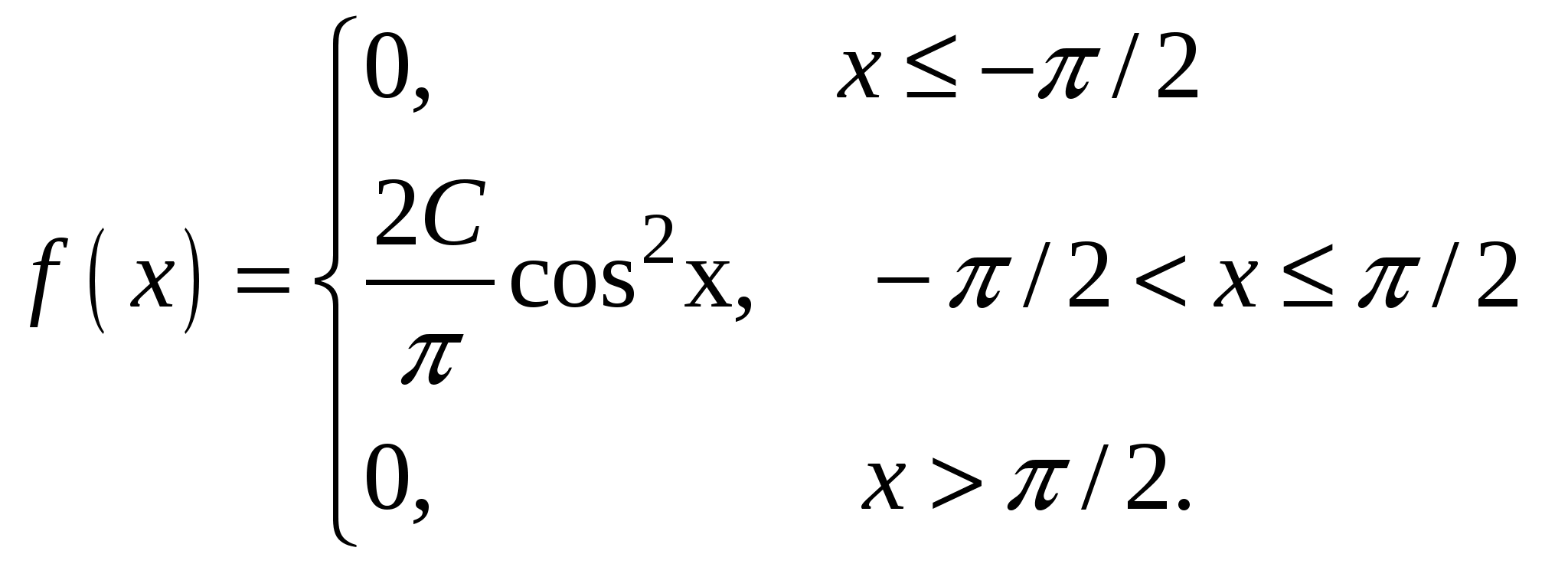
Найти параметр С, функцию распределения F(х) случайной величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (0;/4). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2,2
|
2,4
|
2,6
|
2,8
|
|
У
|
2
|
3
|
4
|
Р
|
0,3
|
0,2
|
0,2
|
0,3
|
|
Р
|
0,1
|
0,4
|
0,5
|
Укажите законы распределения случайной величины Х+У, Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0357 отклонится от математического ожидания менее, чем на 0,7.
Двумерная случайная величина (Х, У) задана таблицей. Найдите её ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
0,5
|
0,01
|
0,06
|
0,15
|
2,3
|
0,03
|
0,11
|
0,07
|
4,8
|
0,09
|
0,09
|
0,04
|
6,3
|
0,31
|
0,02
|
0,02
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.