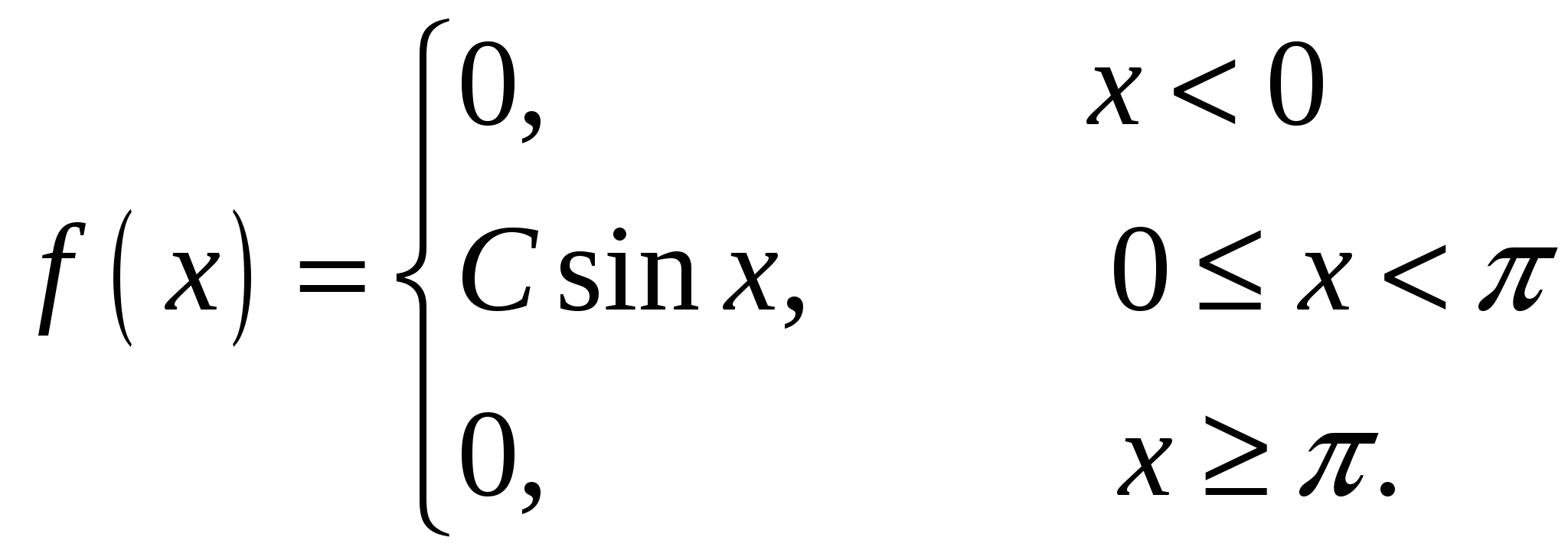Вариант № 17
Сколькими способами можно расставить на полке 7 книг, если a) две определенные книги должны всегда стоять рядом, б) эти две книги не должны стоять рядом?
В урне пять белых и четыре черных шара. Из неё наугад вынимают два шара. Найти вероятность того, что оба шара белые.
В мешочке имеется десять шариков с номерами от 11 до 20. Наудачу извлекают три шарика. Найти вероятность того, что последовательно появятся шарики с номерами 11, 13, 15, если шарики извлекаются: а) без возвращения, б) с возвращением.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,075.
На сборку должно поступить 1000 деталей с первого автомата, 2000 – со второго, 2500 – с третьего. Первый автомат дает 0,3% брака, а второй – 0,2%, третий – 0,4%. Найти вероятность того, что на сборку поступила бракованная деталь.
Что вероятнее: выиграть у равносильного противника (ничейный результат исключается) три партии из четырех или пять из восьми?
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
14 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,4. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,806 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 400 поступивших вызовов имеется 8 сбоев.
Выпущено 1000 билетов денежной лотереи, в которой имеется один выигрыш в 50 рублей, пять – по 25 рублей, десять – по 10 рублей, двадцать пять – по 5 рублей. Составить закон распределения выигрыша на один билет. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
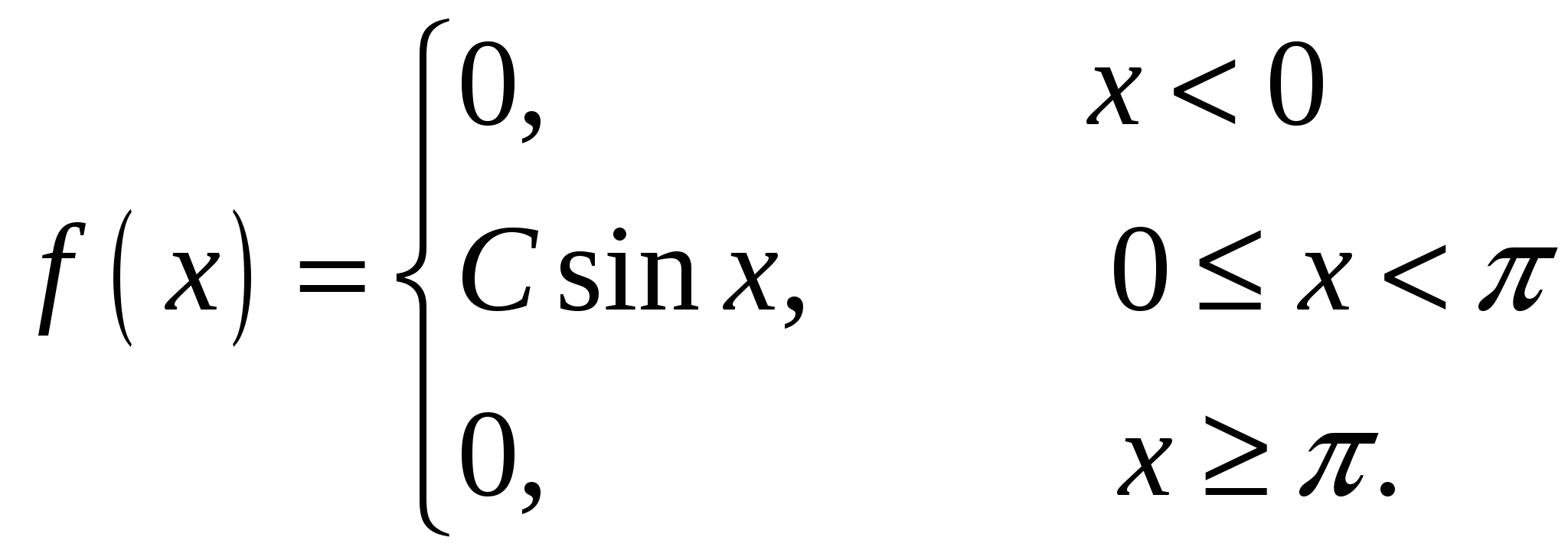
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (0;p/4). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2
|
4
|
6
|
8
|
|
У
|
0,5
|
1,5
|
2,5
|
Р
|
0,3
|
0,4
|
0,2
|
0,1
|
|
Р
|
0,6
|
0,3
|
0,1
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0375 отклонится от своего математического ожидания менее, чем на 0,6.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
0,1
|
0,3
|
0,04
|
0,01
|
1,1
|
0,14
|
0,16
|
0,02
|
2,3
|
0,08
|
0,07
|
0,08
|
3,1
|
0,03
|
0,02
|
0,05
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.