Вариант № 16
Сколькими способами из 5 супружеских пар можно отобрать 4 человека, если: а) в число отобранных должны входить двое мужчин и две женщины; б) никакая супружеская пара не должна входить в их число?
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечено два изделия. Найти вероятность того, что а) из двух изделий одно окрашено, а другое – нет; б) оба изделия окрашены.
Рабочие обслуживают три станка. Вероятность того, что в течение часа станок не потребует ремонта для первого станка равна 0,7; для второго – 0,8; для третьего – 0,85. Найти вероятность того, что в течение часа ремонт потребуется двум станкам.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,064.
При разрыве снаряда образуются крупные, средние, и мелкие осколки в отношении 1:3:6. При попадании в танк крупный осколок пробивает броню с вероятностью 0,9, средний – 0,3, мелкий – 0,1. Какова вероятность того, что попавший в броню осколок пробьёт её?
Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из 800 посеянных семян взойдет не менее 700.
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
13 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,7. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,806 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,07?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 700 поступивших вызовов имеется 8 сбоев.
Из орудия ведется стрельба по плывущему судну с вероятностью попадания при каждом выстреле 0,8. Стрельба ведется до первого попадания или до израсходования всех имеющихся пяти снарядов. Составить закон распределения числа израсходованных снарядов. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
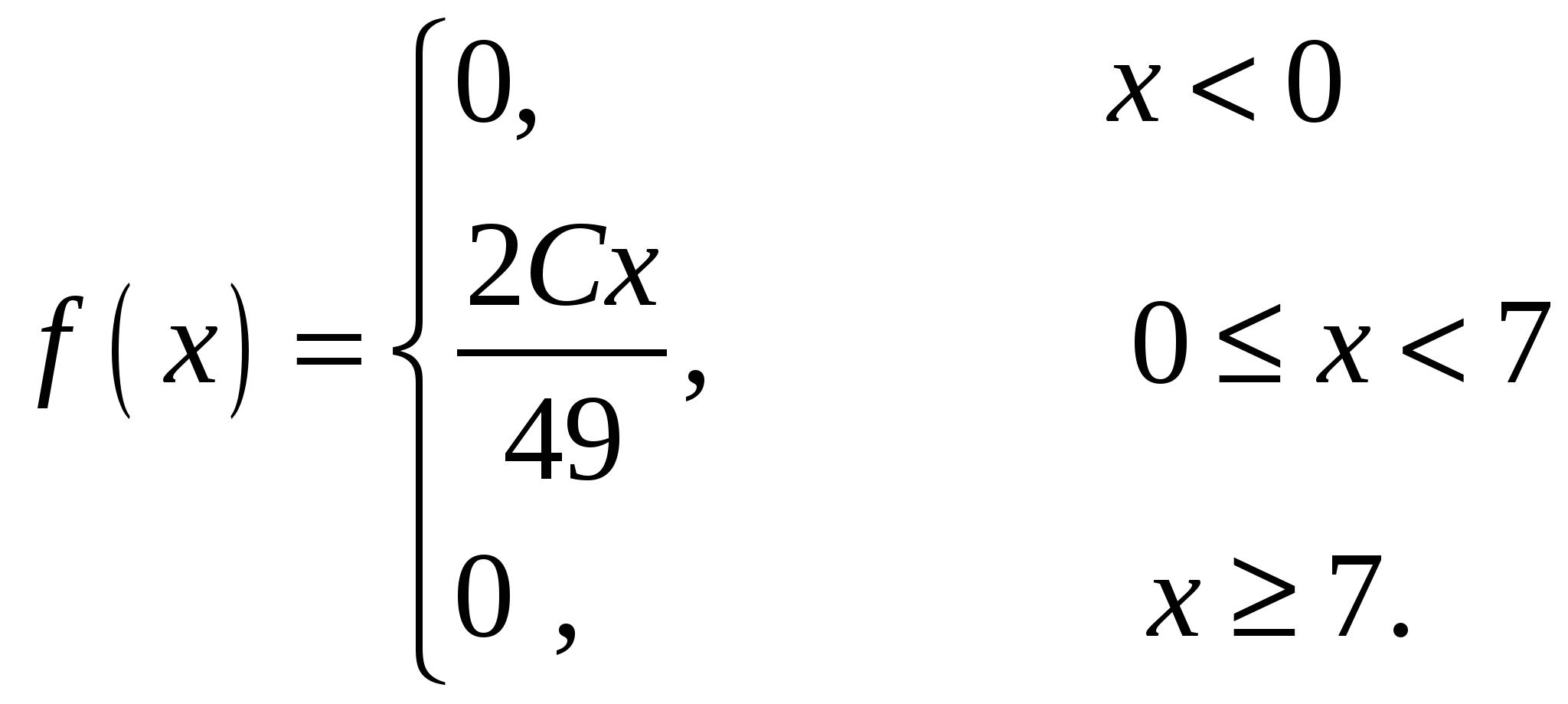
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;5). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-7
|
0
|
4
|
6
|
|
У
|
-3
|
0
|
4
|
Р
|
0,3
|
0,4
|
0,2
|
0,1
|
|
Р
|
0,5
|
0,4
|
0,1
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0364 отклонится от своего математического ожидания менее, чем на 0,4.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
-2
|
-1
|
0
|
1
|
-1
|
1/16
|
2/16
|
1/16
|
1/16
|
0
|
1/16
|
3/16
|
2/16
|
2/16
|
1
|
0
|
1/16
|
2/16
|
2/16
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.