Вариант № 13
Автомобильные номера состоят из одной, двух или трех букв и трех цифр. Найти общее число номеров. Сколько всего номеров, в которых все буквы и цифры различны?
Из колоды карт наудачу вынимают три. Найти вероятность того, что это тройка, семерка, туз.
Три охотника попадают в летящую утку с вероятностями соответственно равными 2/3, 3/4 и 1/4. Они одновременно стреляют по пролетающей утке. Какова вероятность того, что утка будет подбита?
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,07.
В первой коробке содержится 20 радиоламп, 18 из них стандартные, во второй коробке – 10 радиоламп, из них 9 стандартных. Из второй коробки взята наугад одна лампа и переложена в первую коробку, из которой затем наугад берется одна лампа. Найти вероятность того, что эта лампа будет стандартной.
Вероятность появления некоторого события в каждом из независимых испытаний равна 0,6. Найти вероятность того, что это событие наступит ровно 60 раз в 100 испытаниях.
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,6. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,909 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 200 поступивших вызовов имеется 8 сбоев.
По пути следования автомобиля имеется 4 светофора. Каждый из них с вероятностью 0,6 разрешает автомобилю дальнейшее движение. Составить закон распределения числа светофоров, пройденных автомобилем до первой остановки. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
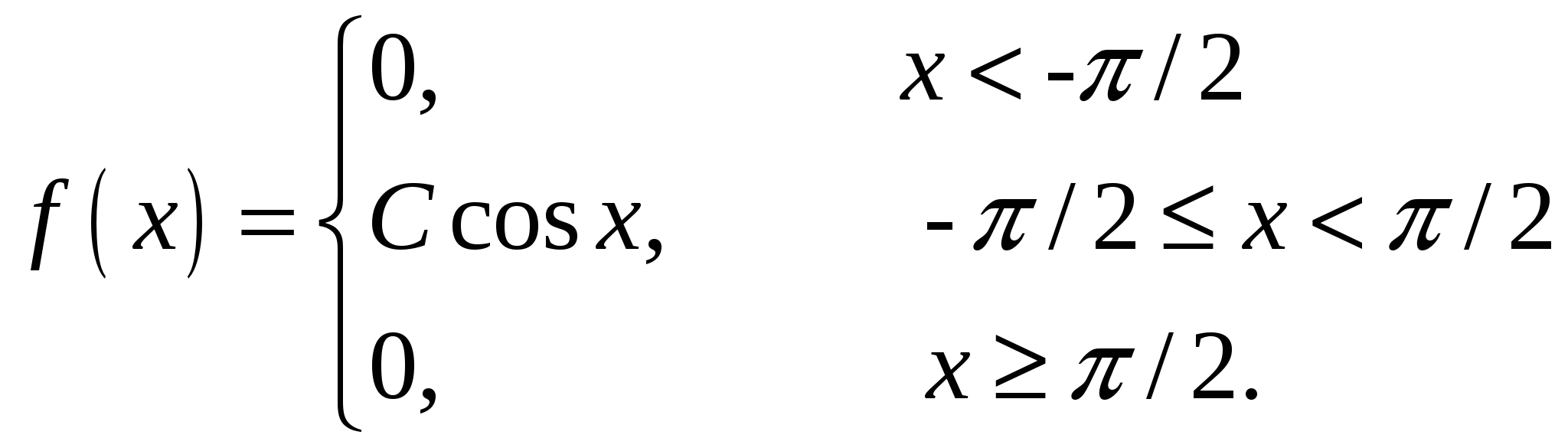
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (p/3;2p/3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-5
|
0
|
1
|
2
|
|
У
|
1
|
7
|
10
|
Р
|
0,3
|
0,3
|
0,2
|
0,2
|
|
Р
|
0,4
|
0,5
|
0,1
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0342 отклонится от своего математического ожидания менее, чем на 0,04.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
-1
|
2
|
3
|
1
|
0,27
|
0,01
|
0,02
|
7
|
0,03
|
0,04
|
0,01
|
18
|
0,01
|
0,03
|
0,02
|
25
|
0,01
|
0,03
|
0,5
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.