Вариант № 10
Танцует компания из семи юношей и десяти девушек. Сколько имеется вариантов участия девушек в танце, если танцуют все кавалеры?
Слово «АГАВА» разрезали на буквы и эти буквы выложили наудачу в ряд. Какова вероятность опять получить это же слово?
Производится четыре независимых выстрела по одной и той же цели с различных расстояний. Вероятности попадания при этих выстрелах соответственно равны 0,2; 0,3; 0,4, 06. Какова вероятность трех попаданий в цель?
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-0,5;1,5]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
В пирамиде восемь винтовок, из которых три снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95, а из винтовки без оптического прицела – 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: он стрелял из винтовки с оптическим прицелом или без него?
В мартеновском цехе металлургического завода не каждая плавка отвечает требованиям, обусловленным в заказе. Поэтому руководство цеха планирует заведомо большее количество плавок. По заказу нужно выполнить 90 плавок, а запланировано 100. Какова вероятность того, что заказ будет выполнен, если вероятность получения качественной плавки равна 0,9?
Вероятность выигрыша в лотерее на 1 билет равна 0,4. Куплено
10 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,2. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9873 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,1?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,011. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения х1 и х2, если известно, что Р(Х=х1)=0,9, М(Х)=3, Д(Х)=0,9 и х1<х2.
Случайная величина Х задана своей плотностью распределения:
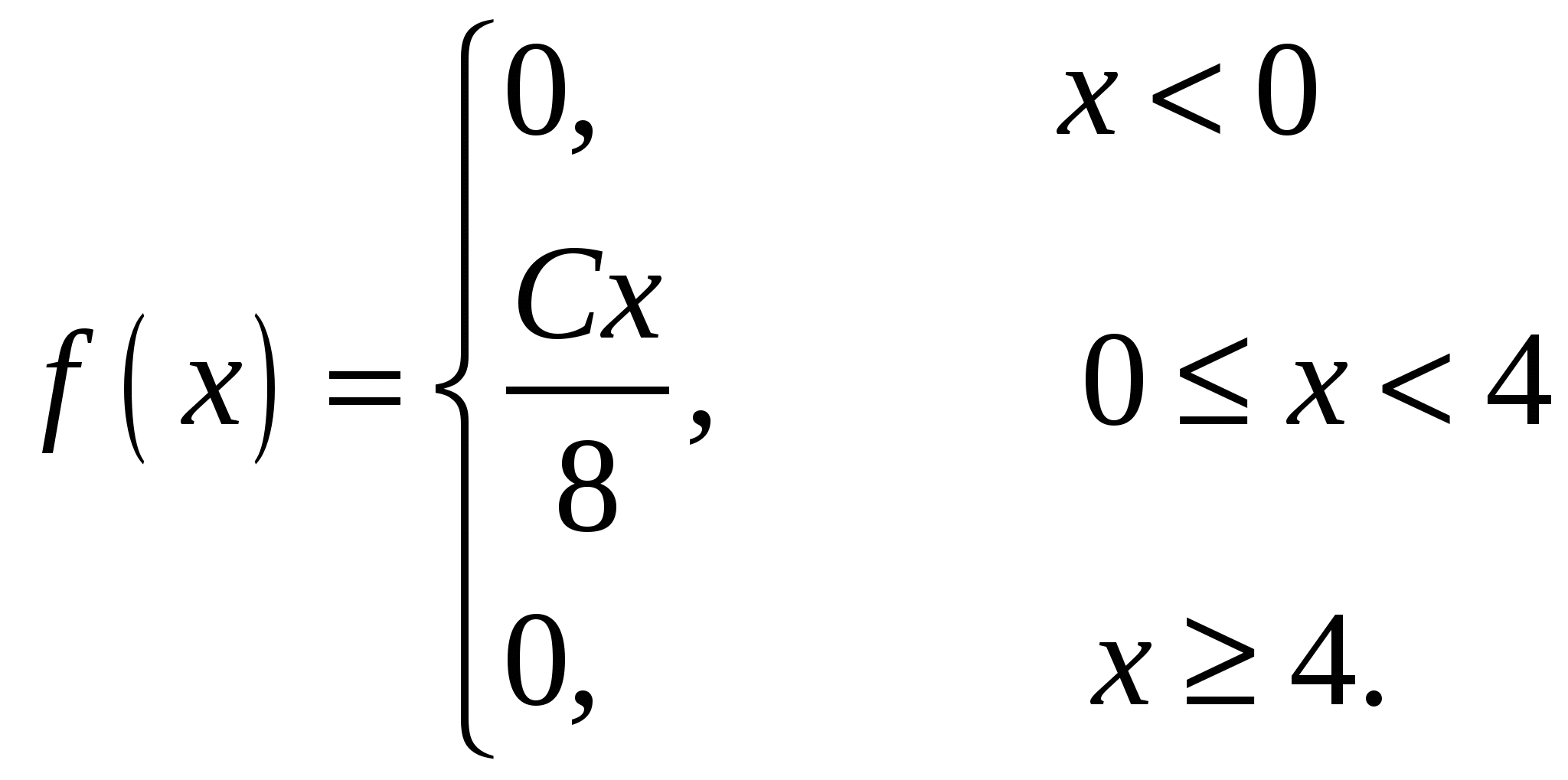
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;8). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2,6
|
3
|
8,3
|
|
У
|
5,2
|
7,6
|
Р
|
0,3
|
0,5
|
0,2
|
|
Р
|
0,6
|
0,4
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0069 отклонится от своего математического ожидания менее, чем на 0,13.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
2
|
4
|
6
|
6,8
|
0,4
|
0,02
|
0,01
|
9,3
|
0,09
|
0,06
|
0,01
|
12,1
|
0,04
|
0,21
|
0,01
|
14,1
|
0,01
|
0,09
|
0,05
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.