Вариант № 7
Номер автомашины состоит из трех букв и трех цифр, причем среди букв используются только двенадцать. Сколько существует различных автомобильных номеров? Сколько таких номеров, в которых цифры не повторяются?
В денежно-вещевой лотерее на каждые 1000 билетов разыгрывается 150 вещевых и 50 денежных выигрыша. Чему равна вероятность выигрыша (безразлично какого, денежного или вещевого) для владельца одного билета?
Из урны, содержащей три белых и два черных шара, взяли наугад два шара и положили в другую урну, содержащую четыре белых и четыре черных шара. Затем, из последней урны наугад взяли один шар. Найти вероятность того, что этот шар белый.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [0;2,5]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
В читальном зале имеется одиннадцать книг, из которых пять –
1960 года издания, четыре – 1970 года издания, две – 1980 года издания. Вероятность ого, что нужная формула есть в книге 1980 года равна 0,7,
в книге 1970 года – 0,8, в книге 1980 года – 0,9. Найти вероятность того, что в наудачу взятой книге нужной формулы нет.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность того, что при ста выстрелах стрелок поразит мишень не менее 75 раз.
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
11 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,6. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,993 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,03?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,08. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Вероятность наличия нужной специалисту книги в каждом из четырех магазинов равна 0,1. Составить закон распределения числа магазинов, которые пришлось посетить с целью покупки нужной книги. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
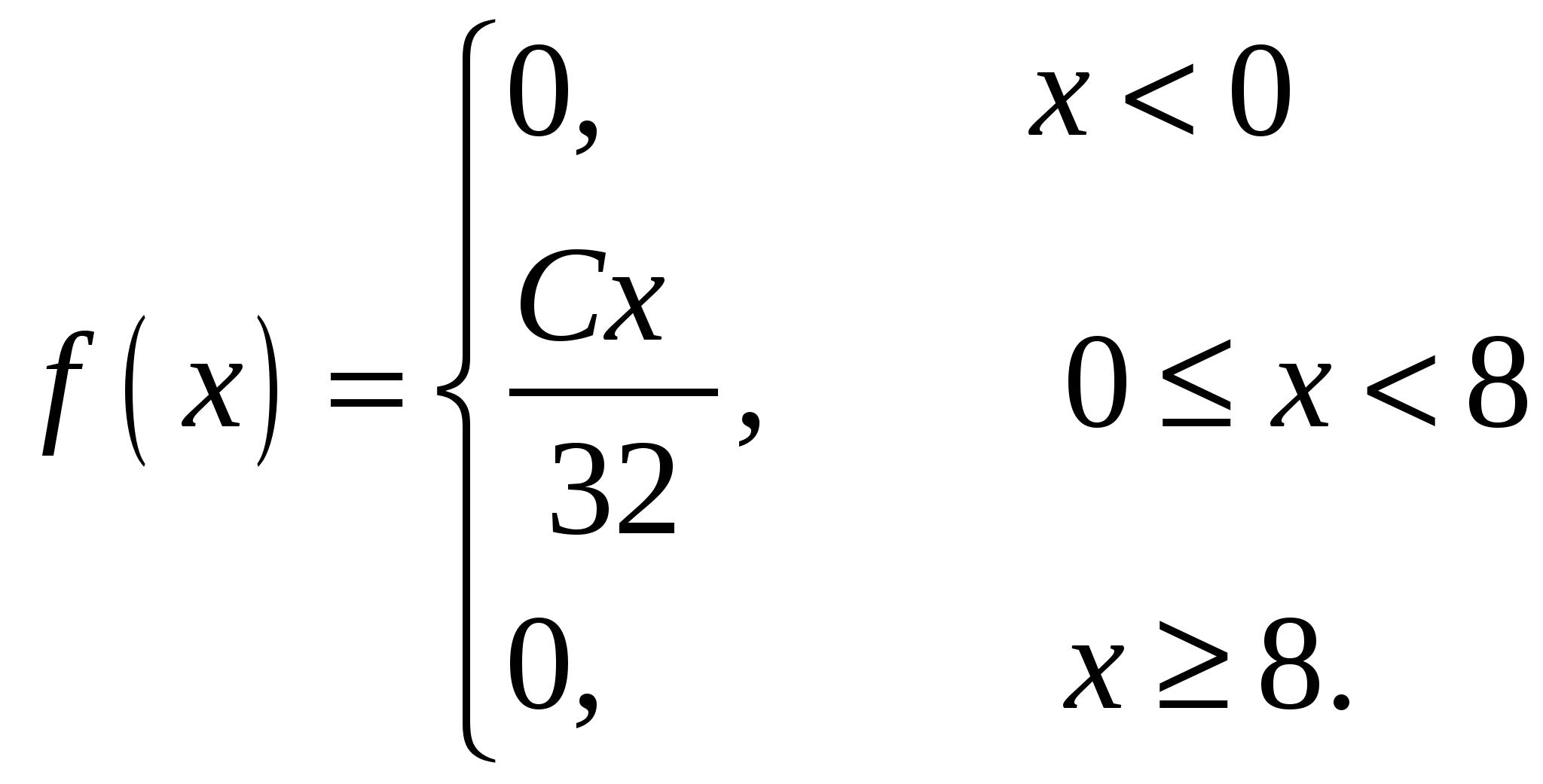
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;10). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-1
|
1
|
2
|
4
|
|
У
|
-3
|
0
|
1
|
Р
|
0,2
|
0,4
|
0,3
|
0,1
|
|
Р
|
0,3
|
0,5
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,159 отклонится от своего математического ожидания менее, чем на 0,3.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
3
|
5
|
1,2
|
0,4
|
0,01
|
0,01
|
8,8
|
0,06
|
0,08
|
0,01
|
14
|
0,04
|
0,03
|
0,02
|
20
|
0,03
|
0,01
|
0,3
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.