Вариант № 5
Докажите, что число трехбуквенных слов, которые можно образовать из букв слова «гипотенуза», равно числу всевозможных перестановок букв слова «призма».
10 книг на одной полке расставлены наудачу. Определить вероятность того, что при этом три определенных книги окажутся поставленными рядом.
В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному кубику три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются а) без возвращения, б) с возвращением.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-1;2]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
На склад поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 46%, третьей – 34%. Известно, что средний процент нестандартных деталей для первой фабрики равен 3%, для второй – 2%, для третьей – 1%. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось нестандартным.
Производится шесть выстрелов по цистерне с горючим. Вероятность попадания при одном выстреле равна 0,2. Первое попадание дает пробоину и вызывает течь, а второе – воспламенение горючего. Найти вероятность того, что цистерна будет подожжена.
Вероятность выигрыша в лотерее на 1 билет равна 0,3. Куплено
11 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,3. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9624 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,01?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,006. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения х1 и х2, если известно, что Р(Х=х1)=0,2, М(Х)=2,6, Д(Х)=0,64 и х1<х2.
Случайная величина Х задана своей плотностью распределения:
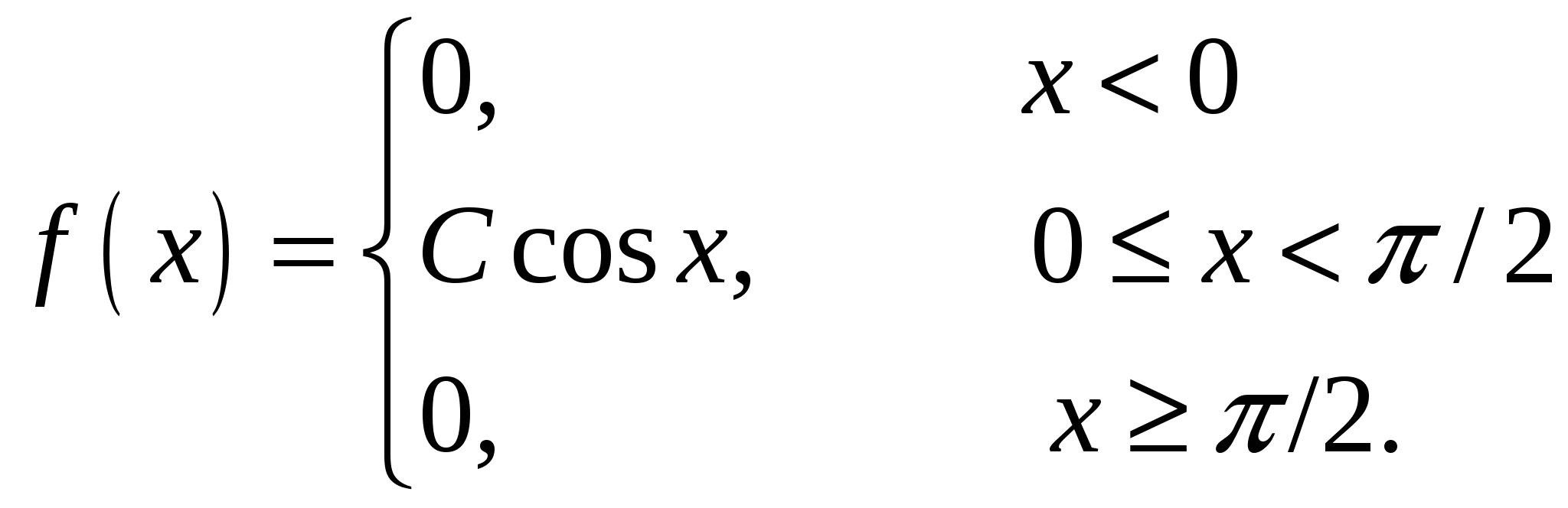
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (0;/3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
0
|
1
|
2
|
3
|
|
У
|
-1
|
0
|
1
|
Р
|
0,1
|
0,3
|
0,4
|
0,2
|
|
Р
|
0,3
|
0,3
|
0,4
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0372 отклонится от своего математического ожидания менее, чем на 0,12.
Двумерная дискретная случайная величина (Х, У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
3
|
4
|
5
|
2
|
0,4
|
0,02
|
0,01
|
3
|
0,08
|
0,03
|
0,01
|
4
|
0,01
|
0,3
|
0,02
|
5
|
0,01
|
0,05
|
0,06
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.