Вариант № 4
Некто имеет восемь пар перчаток. Сколькими способами он может выбрать одну перчатку для правой руки и одну для левой так, чтобы они не принадлежали одной паре?
В ящике имеется 15 годных и 5 бракованных деталей. Найти вероятность того, что среди трех наугад вынутых из ящика деталей будут две бракованные.
Для некоторой местности среднее число ясных дней в июле равно 25. Найти вероятность того, что первые два дня июля будут ясными.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-2;1]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
Стрельба производится по пяти мишеням типа А, трем типа Б и двум типа С. Вероятность попадания в мишень типа А равна 0,4; типа Б – 0,1, типа С – 0,15. Найти вероятность поражения мишени при одном выстреле, если неизвестно, в мишень какого типа он будет сделан.
В цехе имеется пять моторов. Вероятность быть включенным в данный момент для каждого из них равна 0,8. Найти вероятность того, что из них в данный момент включены: а) четыре мотора; б) не менее двух моторов; в) хотя бы один мотор.
Вероятность выигрыша в лотерее на 1 билет равна 0,3. Куплено
12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,6. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9642 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,03?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,005. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Известно, что в партии из 20 телефонных аппаратов имеется пять не действующих. Из этой партии наугад взято четыре аппарата. Составить закон распределения числа не действующих из них аппаратов. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
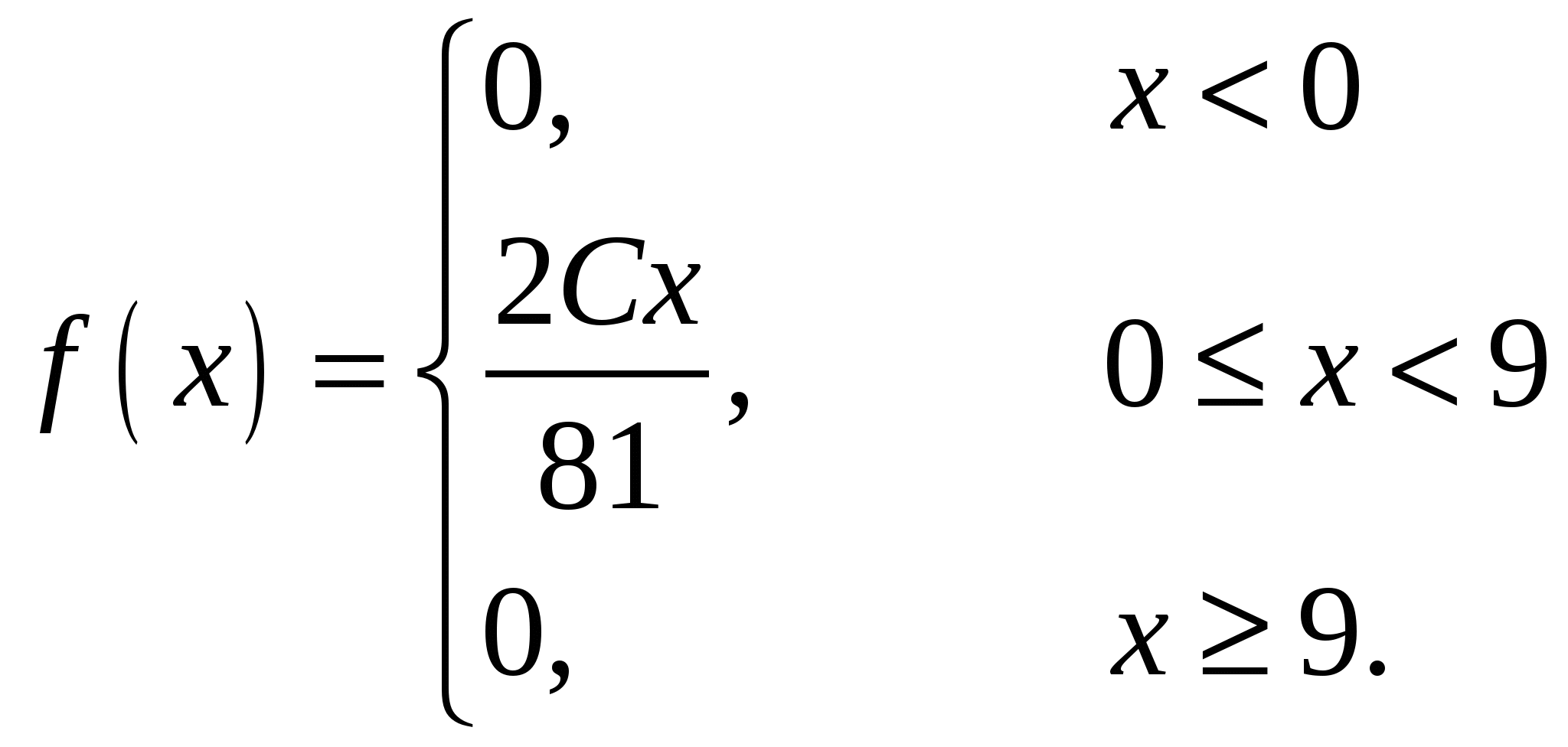
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;7). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2,3
|
2,5
|
2,7
|
2,9
|
|
У
|
1
|
2
|
3
|
Р
|
0,4
|
0,3
|
0,2
|
0,1
|
|
Р
|
0,3
|
0,5
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0162 отклонится от своего математического ожидания менее, чем на 0,14.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
1,5
|
0,03
|
0,02
|
0,02
|
2,9
|
0,06
|
0,13
|
0,03
|
4,1
|
0,4
|
0,04
|
0,02
|
5,6
|
0,15
|
0,06
|
0,04
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.