Вариант № 6
В автомашине семь мест. Сколькими способами можно разместить семь человек в этой машине, если занять место водителя могут только трое из них?
В лотерее 1000 билетов, из них на один билет выпадает выигрыш 500 рублей, на 10 билетов – по 100 рублей, на 50 – по 20 рублей, остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выигрыша не менее 50 рублей.
Три стрелка стреляют в цель независимо друг от друга. Вероятности попадания в цель для первого стрелка равна 0,6, для второго – 0,7, для третьего 0,75. Найти вероятность по крайней мере одного попадания в цель, если каждый стрелок делает по одному выстрелу.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [0;3]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квалификационную норму для лыжника – 0,9, для велосипедиста – 0,8, для бегуна – 0,75. Найти вероятность того, что взятый наудачу из этой группы спортсмен выполнит норму.
Вероятность того, что расход электроэнергии за сутки не превысит нормы равна 0,75. Найти вероятность того, что из ближайших 6 суток только 4 суток пройдут без перерасхода энергии.
Вероятность выигрыша в лотерее на один билет равна 0,3. Куплено 15 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую ему вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,6. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,933 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,007. Определить вероятность того, что среди 100 поступивших вызовов имеется 7 сбоев.
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 рублей и десять – по 1 рублю. Найти закон распределения суммы возможного выигрыша для владельца одного билета и найти его средний выигрыш.
Случайная величина Х задана своей плотностью распределения:
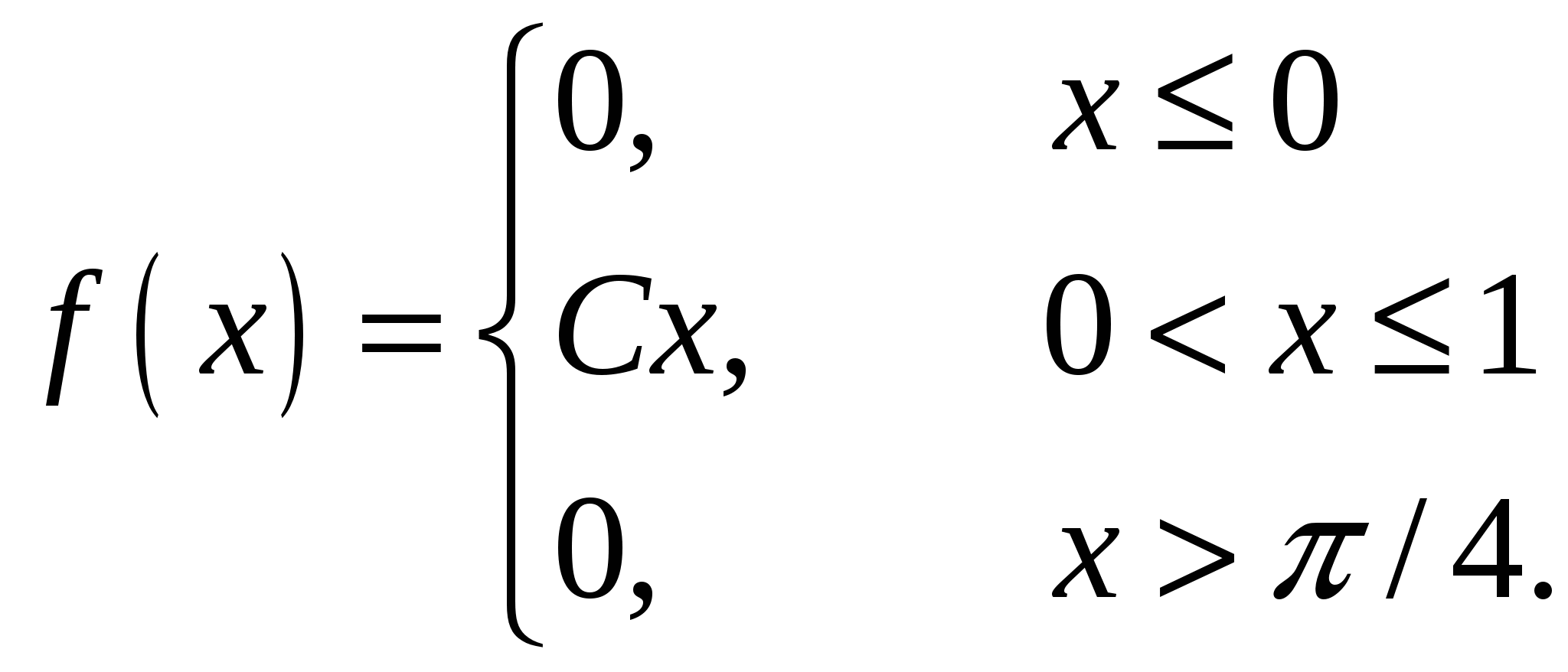
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (0,5;1). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-2
|
1
|
5
|
7
|
|
У
|
-2
|
1
|
3
|
Р
|
0,2
|
0,1
|
0,5
|
0,2
|
|
Р
|
0,3
|
0,5
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,001 отклонится от своего математического ожидания менее, чем на 0,2.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
0,3
|
0,4
|
0,01
|
0,01
|
2,25
|
0,09
|
0,2
|
0,01
|
4,1
|
0,06
|
0,08
|
0,1
|
6,5
|
0,01
|
0,02
|
0,01
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.