Вариант № 8
Сколько нужно издать словарей, чтобы можно было непосредственно переводить с одного из пяти языков на другой?
В группе 17 юношей и 8 девушек. Какова вероятность того, что студент, фамилия которого первая в списке окажется девушкой?
Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует наладки, равна 0,8 для первого станка, 0,3 – для второго станка, 0,9 – для третьего станка. Найти вероятность того, что в течение часа только один станок потребует наладки.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-1;3]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
В ящик, содержащий три одинаковые детали, брошена стандартная деталь, а затем из него наудачу извлечена деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.
Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 50 и не более 80 раз.
Вероятность выигрыша в лотерее на один билет равна 0,4. Куплено 13 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую ему вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,3. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,996 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,009. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Монета брошена 3 раза. Найти закон распределения числа выпадения «герба», математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
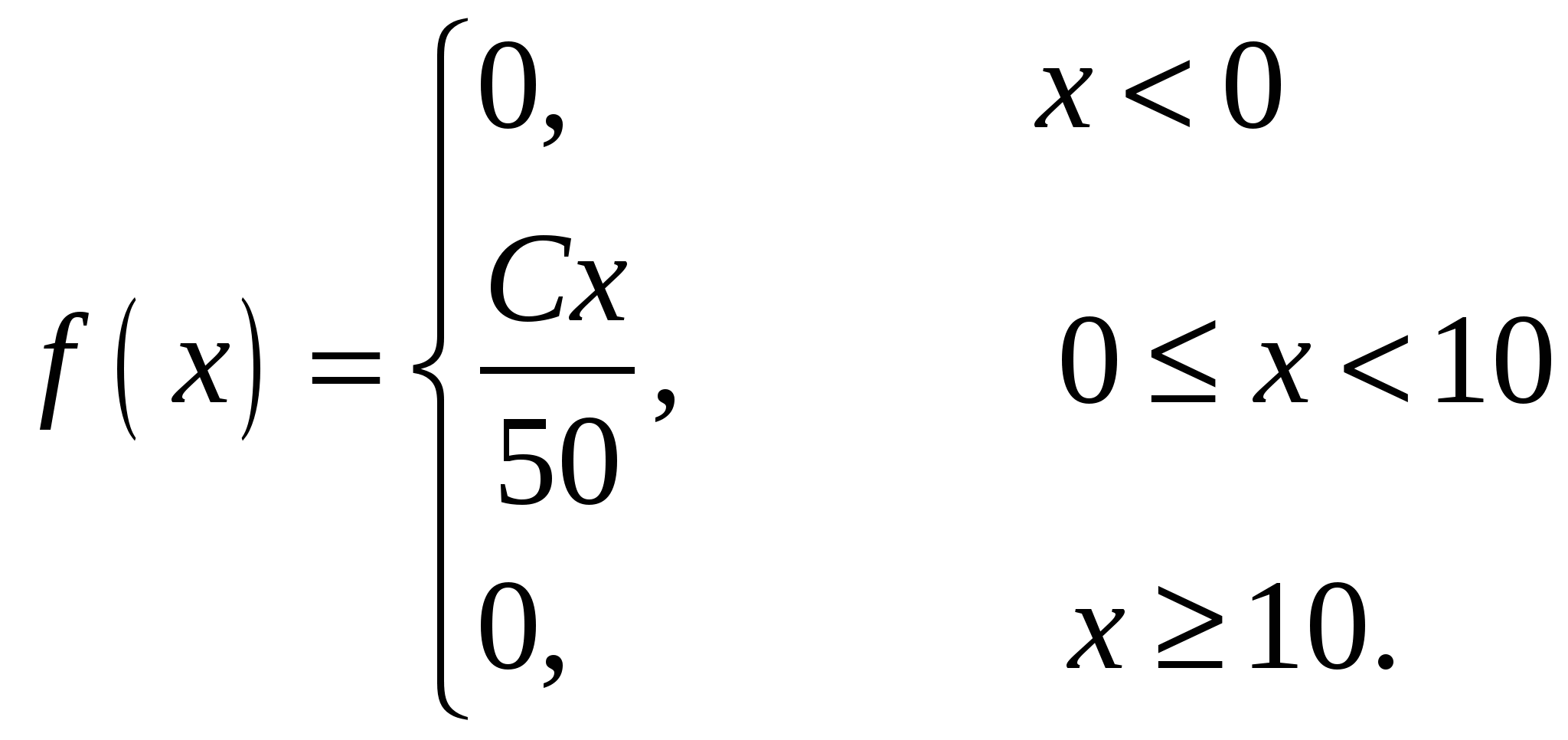
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;10). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
3
|
5
|
7
|
|
У
|
2
|
6
|
Р
|
0,3
|
0,5
|
0,2
|
|
Р
|
0,6
|
0,4
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,168 отклонится от своего математического ожидания менее, чем на 0,4.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
0,8
|
0,15
|
0,04
|
0,11
|
2,9
|
0,07
|
0,43
|
0,02
|
5,1
|
0,04
|
0,04
|
0,04
|
8
|
0,01
|
0,02
|
0,03
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.