Вариант № 11
Предположим, что 15 студентов могут явиться для сдачи зачета в один из трех дней, указанных им. а) Сколькими способами могут распределиться студенты по дням явки на зачет? б) Сколько будет способов распределиться, если в каждый день будет приходить равное число студентов (считаем, что каждый сдаёт зачет один раз)?
В партии 10 деталей, из них 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.
Два стрелка независимо друг от друга стреляют по мишени, причем каждый делает по два выстрела. Для первого стрелка вероятность попадания в цель при одном выстреле равна 0,7, для второго – 0,9. Найти вероятность того, что мишень будет поражена только два раза.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,09.
Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,06, на втором – 0,09. Производительность второго автомата вдвое больше, чем первого. Найти вероятность того, что наудачу взятая с конвейера деталь будет нестандартной.
Принимая одинаково вероятным рождение мальчика и девочки,
найти вероятность того, что среди 4500 новорожденных будет 2300 мальчиков.
Вероятность выигрыша в лотерее на 1 билет равна 0,4. Куплено
12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,8. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9127 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,05?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 200 поступивших вызовов имеется 8 сбоев.
Производится последовательно испытания четырех приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался ненадежным. Построить ряд распределения числа испытанных приборов, если вероятность выдержать испытание для каждого прибора равна 0,9. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
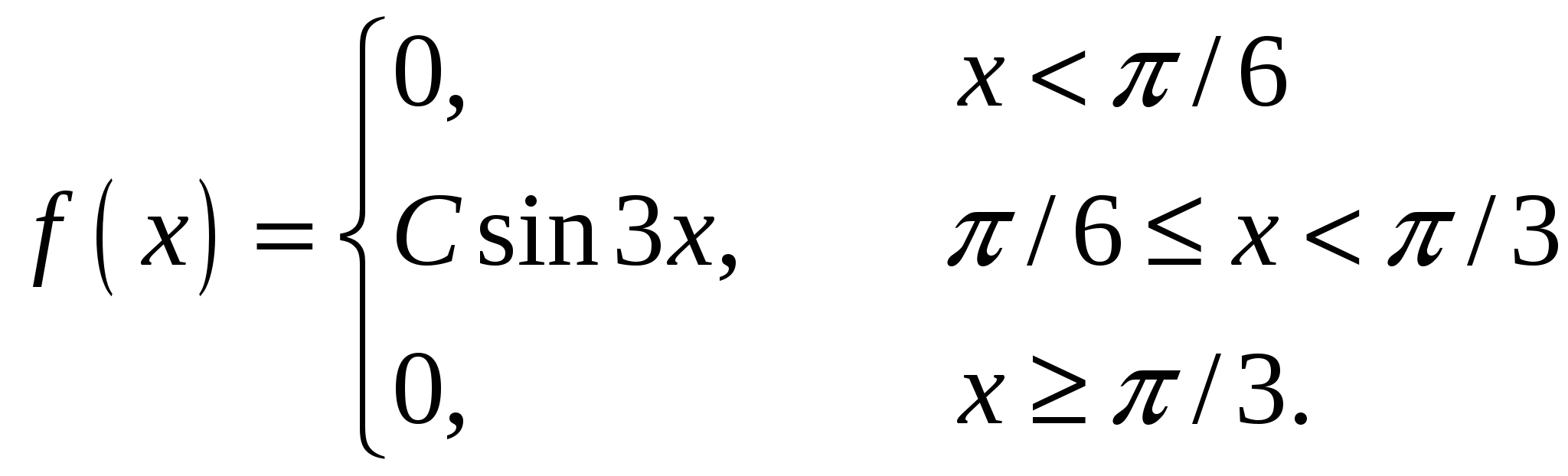
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (/4;/2). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-2
|
-1
|
|
У
|
0
|
1
|
2
|
Р
|
0,3
|
0,7
|
|
Р
|
0,2
|
0,6
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0324 отклонится от своего математического ожидания менее, чем на 0,018.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
3
|
0,3
|
0,01
|
0,01
|
5
|
0,2
|
0,03
|
0,01
|
7,1
|
0,05
|
0,29
|
0,01
|
11
|
0,01
|
0,04
|
0,04
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.