Расчетно-графическое задание Вариант № 1
В урне имеется 10 шаров: 7 черных и 3 белых. Из урны наугад вынимается два шара. Сколькими различными способами это можно сделать? Сколько существует способов вынуть при этом два черных шара; два шара разного цвета?
На каждой из пяти одинаковых карточек написана одна из следующих букв: О, П, Р, С, Т. Найти вероятность того, что на удачу вынутых по одной и расположенных в одну линию карточках можно будет прочесть слово «СПОРТ».
Экспедиция издательства отправила газеты в два почтовых отделения. Вероятность своевременной доставки газет в каждое из почтовых отделений равна 0,9. Найти вероятность того, что а) только одно почтовое отделение получит газеты вовремя, б) хотя бы одно почтовое отделение получит газеты вовремя.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-1;1]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,5, для второй – 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошибка допущена первой перфораторщицей.
На склад магазина поступают изделия, из которых 80% оказываются высшего сорта. Найти вероятность того, что из 100 взятых наудачу изделий не менее 85 окажется высшего сорта.
Вероятность выигрыша в лотерее на 1 билет равна 0,3. Куплено 10 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,6. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,933 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,01?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 1000 поступивших вызовов имеется 7 сбоев.
Стрелок ведет стрельбу по мишени до первого попадания, имея
4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Найти закон распределения числа патронов, оставшихся неизрасходованными. Найти математическое ожидание и дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
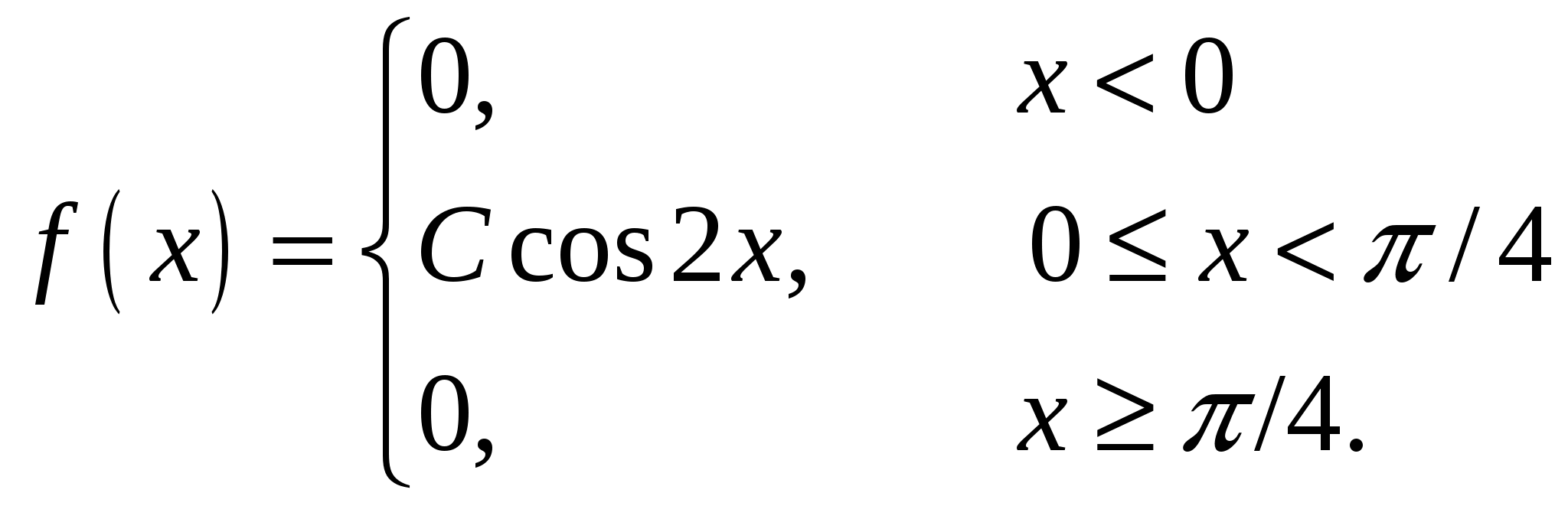
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал
(-/3;/6). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
-4
|
-3
|
-2
|
1
|
|
У
|
1
|
3
|
5
|
Р
|
0,1
|
0,4
|
0,3
|
0,2
|
|
Р
|
0,3
|
0,4
|
0,3
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,004 отклонится от своего математического ожидания менее, чем на 0,2.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
5
|
0,01
|
0,01
|
0,01
|
6
|
0,4
|
0,04
|
0,02
|
7
|
0,02
|
0,3
|
0,02
|
8
|
0,01
|
0,02
|
0,14
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.