Вариант № 2
В команду КВН института нужно представить двух участников от группы – одну девушку и одного юношу. Сколькими различными способами это можно сделать, если в группе из 26 человек 12 девушек?
В вещевой лотерее разыгрывается 5 предметов. Всего в урне 30 билетов. Каждый подошедший к урне наудачу вынимает 4 билета. Какова вероятность того, что 2 из этих билетов окажутся выигрышным?
Три баскетболиста должны произвести по одному броску мяча. Вероятности попадания мяча в корзину для первого, второго и третьего баскетболистов соответственно равны 0,9; 0,8 и 0,7. Найти вероятность того, что удачно произвел бросок только один из них.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [-1;0]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
Некоторое изделие может поступать для обработки в случайном порядке на один из трех автоматов с вероятностями 0,2; 0,3 и 0,5. При обработке на первом автомате вероятность брака равна 0,02, на втором – 0,03, на третьем – 0,05. Найти вероятность того, что поступившее после обработки в цех изделие окажется без брака.
Вероятность того, что в данный день торговая база уложится в норму расходов на транспорт равна 3/4. Какова вероятность того, что лишь в один из дней шестидневной рабочей недели база уложится в норму расходов на транспорт.
Вероятность выигрыша в лотерее на один билет равна 0,8. Куплено 14 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую ему вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,3. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,996 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,3?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,03. Определить вероятность того, что среди 1000 поступивших вызовов имеется 9 сбоев.
В двух урнах находится по 5 пронумерованных шаров. В первой урне 2 шара имеют номер 1, три шара – номер 2. Во второй урне три шара имеют номер 1, два шара – номер 2. Из этих урн берут наугад по одному шару и находят произведение их номеров. Получившееся число есть случайная величина. Найти математическое ожидание и дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
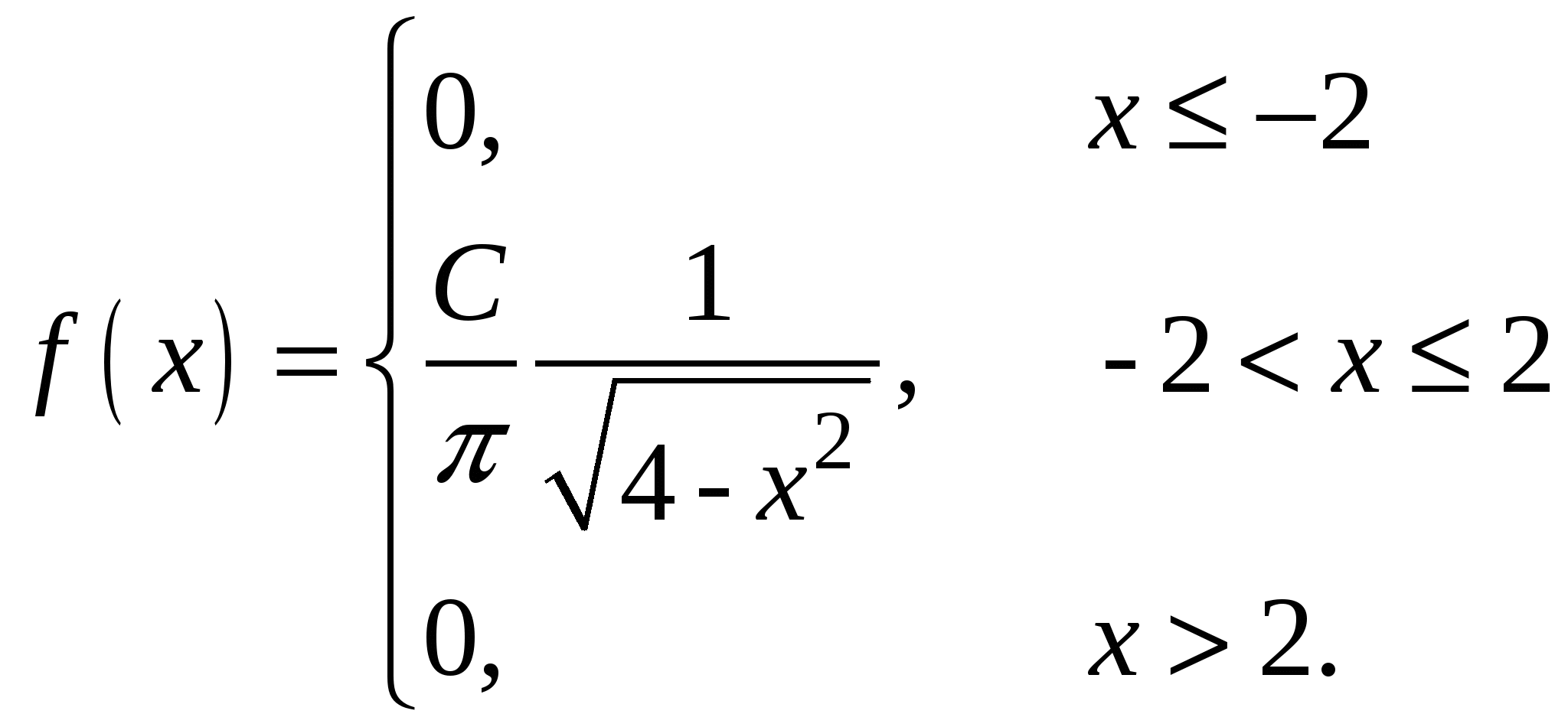
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал(-1;1). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
3
|
4
|
5
|
|
У
|
2
|
3
|
4
|
5
|
Р
|
0,1
|
0,4
|
0,5
|
|
Р
|
0,1
|
0,1
|
0,5
|
0,3
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,009 отклонится от своего математического ожидания менее, чем на 0,2.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
4
|
0,5
|
0,04
|
0,01
|
6
|
0,03
|
0,04
|
0,01
|
8
|
0,01
|
0,03
|
0,02
|
10
|
0,01
|
0,03
|
0,27
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.