Вариант № 15
В эксперименте по изучению поведения животных крыса бежит по лабиринту, который устроен так, что сначала она должна выбрать одну из 2-х дверей. За каждой из них ее ожидает по три двери, а за каждой из них – по четыре. Пройдя через какую-либо дверь, крыса не может вернуться через нее обратно. Сколькими различными путями крыса может пройти лабиринт от начала до конца?
На тепловой электростанции 15 сменных инженеров, из них 3 женщины. В смену занято 3 человека. Найти вероятность того, что в случайно набранную смену попали двое мужчин и одна женщина.
Для сигнализации об аварии установлены 2 независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95, для второго она равна 0,9. Найти вероятность того, что при аварии сработает только один сигнализатор.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,5.
В собранной электрической цепи может быть поставлен предохранитель первого типа, который при перегрузке срабатывает с вероятностью 0,6 или предохранитель второго типа, который при перегрузке срабатывает с вероятностью 0,4. Предохранитель в цепи сработал. Что вероятнее: поставлен предохранитель первого типа или второго?
Средний процент нарушений работы кинескопа телевизора в течение гарантийного срока 10%. Вычислить вероятность того, что из 20 телевизоров более 18 выдержат гарантийный ремонт.
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
17 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,9. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9904 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,05?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,02. Определить вероятность того, что среди 300 поступивших вызовов имеется 8 сбоев.
В лотерее, содержащей 100 билетов, разыгрывается мотоцикл стоимостью 250 рублей, велосипед – 50 рублей, часы – 40 рублей. Составить закон распределения выигрыша по одному билету. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
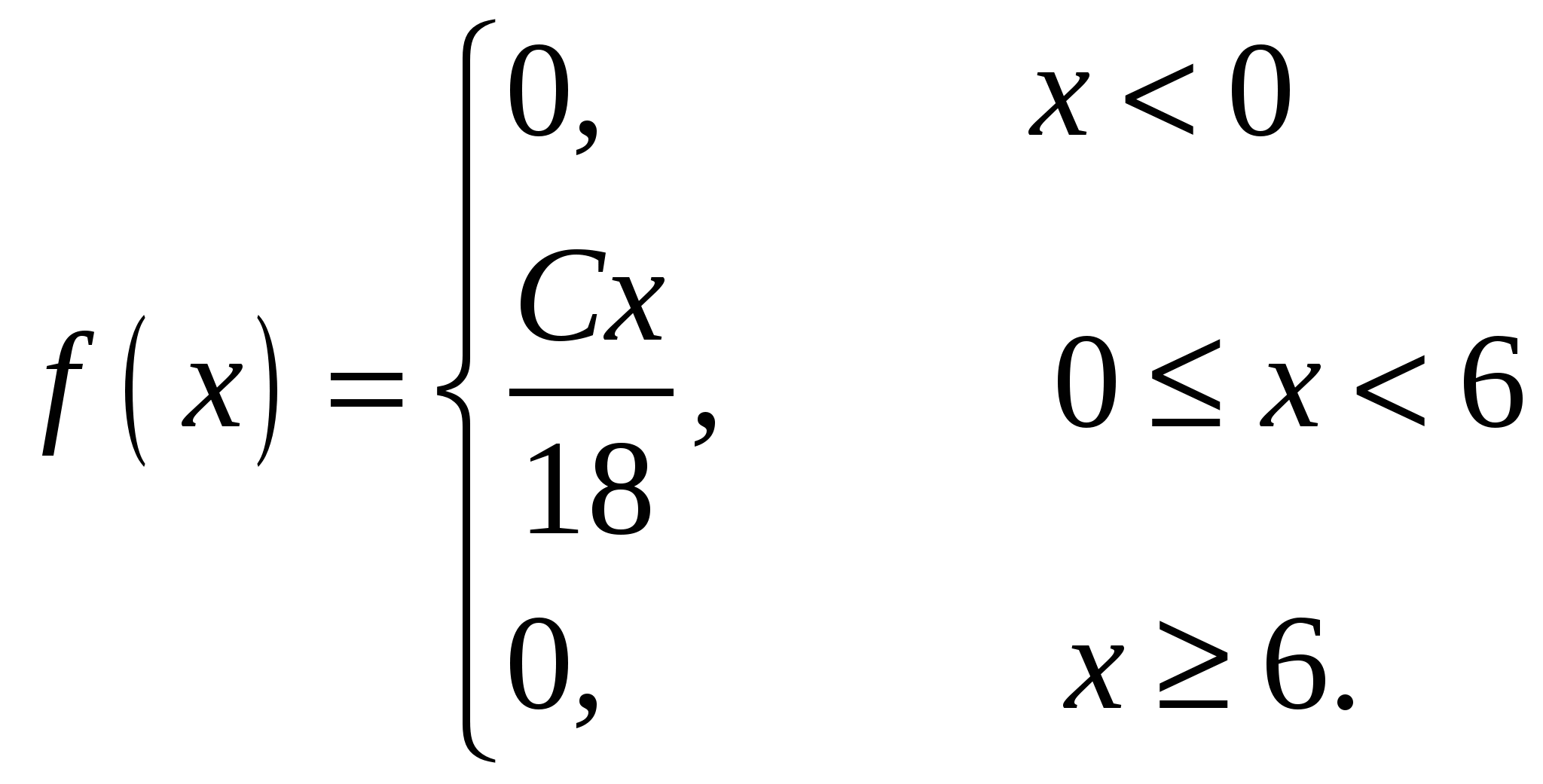
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2; 5). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
5
|
10
|
15
|
20
|
|
У
|
3
|
5
|
7
|
Р
|
0,1
|
0,4
|
0,3
|
0,2
|
|
Р
|
0,2
|
0,6
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0341 отклонится от своего математического ожидания менее, чем на 0,02.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
-3
|
1
|
2
|
5
|
0,03
|
0,02
|
0,02
|
9
|
0,4
|
0,15
|
0,03
|
14
|
0,02
|
0,04
|
0,06
|
16
|
0,13
|
0,06
|
0,04
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.