Вариант № 18
Каких чисел от 1 до 10 000 будет больше: тех, в записи которых встречается единица, или тех, в записи которых ее нет?
На экзамене студенту предлагается 20 билетов, в каждом по три вопроса. Из 60 вопросов, вошедших в билеты, студент знает 50. Какова вероятность того, что взятый студентом билет будет состоять из двух известных и одного неизвестного ему вопроса?
В урне 3 белых и 3 черных шара. Из урны наугад последовательно вынимают 2 шара, не возвращая их обратно. Найти вероятность того, что второй извлеченный шар белый, если первым был черный шар.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,69.
При передаче сообщения сигнальных «точка» и «тире» эти сигналы встречаются в соотношении 5:3. Статистические свойства помех таковы, что искажают в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире». Найти вероятность того, что принятый сигнал не искажен.
В приборе шесть одинаковых предохранителей. Для каждого из них вероятность перегореть после 1000 часов работы равна 0,4. Если перегорело не менее двух предохранителей, то прибор требует ремонта. Найти вероятность того, прибор потребует ремонта после 1000 часов работы, если предохранители перегорают независимо друг от друга.
Вероятность выигрыша в лотерее на 1 билет равна 0,5. Куплено
15 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,3. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9573 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,02?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 900 поступивших вызовов имеется 8 сбоев.
Среди 30 измерительных приборов имеется 6 недостаточно точных. Работники ОТК наудачу берут одновременно 2 прибора. Составить закон распределения числа точных приборов среди отобранных. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
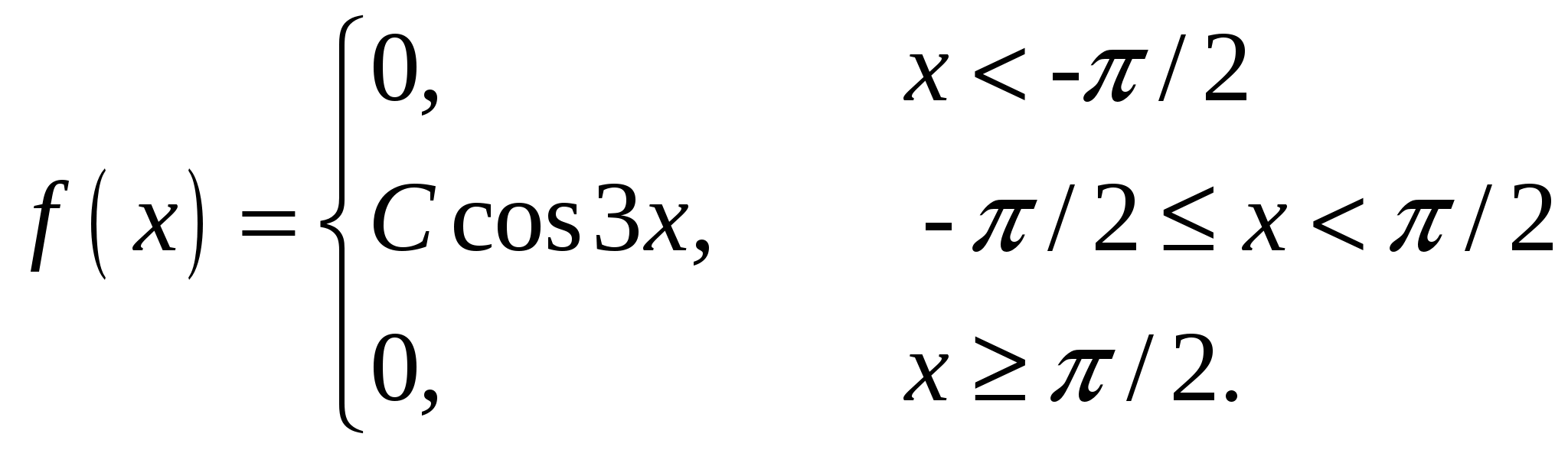
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал
(-/3; p/3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
0,2
|
0,4
|
0,6
|
0,8
|
|
У
|
1
|
2
|
3
|
Р
|
0,1
|
0,3
|
0,1
|
0,5
|
|
Р
|
0,6
|
0,3
|
0,1
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0274 отклонится от своего математического ожидания менее чем на 0,16.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
-3
|
-4
|
2
|
2
|
0,3
|
0,02
|
0,01
|
3
|
0,08
|
0,03
|
0,01
|
4
|
0,06
|
0,4
|
0,02
|
5
|
0,01
|
0,05
|
0,01
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.