Вариант № 21
Десять различных книг расставлены на полке наудачу. Определить число способов, в которых три определенные книги окажутся поставленными вместе.
В студенческой группе 25 человек, из них 10 девушек. От группы надо послать трех представителей на некоторое мероприятие. Представителей решено выбрать по жребию. Какова вероятность того, что по жребию будут выбраны 2 юноши и 1 девушка?
Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.
Наудачу взяты 2 положительных числа Х и У, каждое их них не превышает трех. Найти вероятность того, что произведение ХУ будет не больше 2, а частное Х/У не больше 3.
Сборщик получил 3 коробки деталей, изготовленных заводом № 1 и
2 коробки, изготовленные заводом №2. Вероятность того, что деталь завода № 1 стандартна равна 0,8, а завода № 2 – 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
Многие ботаники делали опыты по скрещиванию желтого (гибридного) гороха. Вероятность появления зеленого гороха в таких опытах равна 0,25. Какова вероятность того, что при 31153 скрещиваниях зеленый горох будет получен от 7659 до 8493 раз?
Вероятность выигрыша в лотерее на 1 билет равна 0,6. Куплено
12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,2. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9232 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,04?
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,004. Определить вероятность того, что среди 500 поступивших вызовов имеется 9 сбоев.
В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных. Найти математическое ожидание, дисперсию, функцию распределения этой случайной величины.
Случайная величина Х задана плотностью распределения:
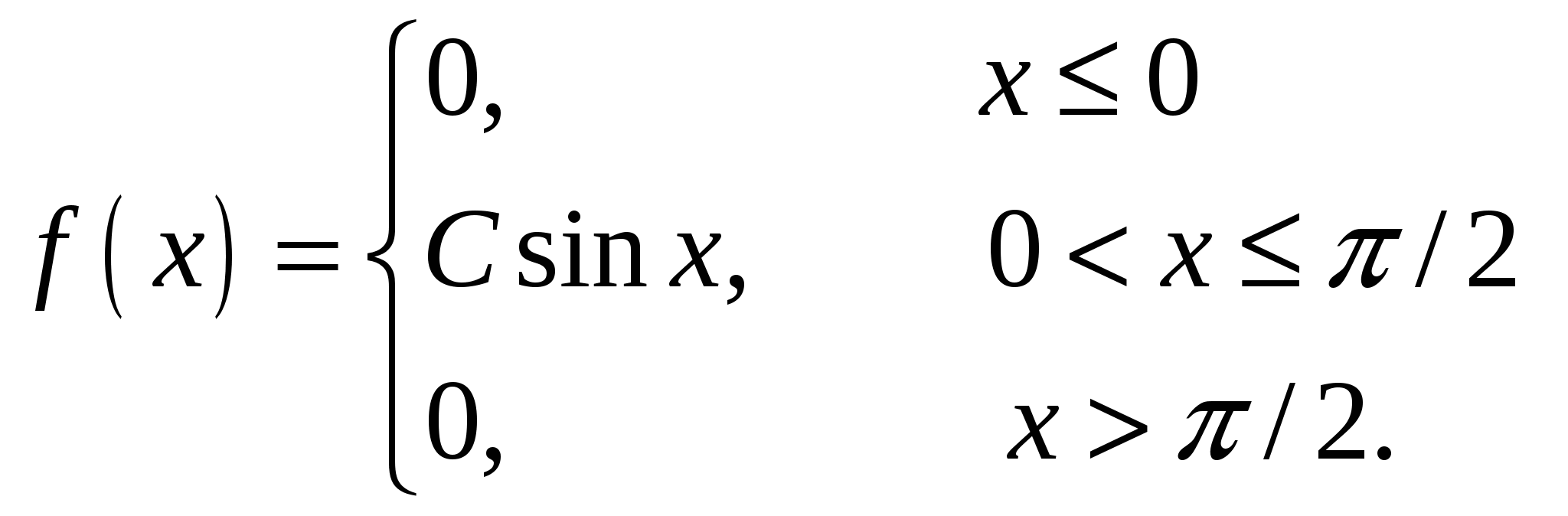
Найти параметр С, функцию распределения F(х) случайной величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (/6;/3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
1,2
|
1,5
|
1,8
|
2,1
|
|
У
|
3
|
7
|
11
|
Р
|
0,4
|
0,3
|
0,2
|
0,1
|
|
Р
|
0,5
|
0,3
|
0,2
|
Укажите законы распределения случайной величины Х+У, Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,016 отклонится от математического ожидания менее, чем на 0,3.
Двумерная случайная величина (Х, У) задана таблицей. Найдите её ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
4
|
1
|
0,02
|
0,01
|
0,01
|
8
|
0,06
|
0,08
|
0,01
|
14
|
0,04
|
0,03
|
0,4
|
20
|
0,3
|
0,01
|
0,03
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.