Вариант № 29
Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Сколько имеется различных способов составить “слово” из этих четырех букв? В скольких случаях при случайном расположении букв в ряд он получит слово МАМА?
В группе 15 студентов, из них 7 девушек группе нужно послать 5 человек на собрание. Найти вероятность того, что пойдут а) три юноши и две девушки; б) один юноша.
Вероятности, что разговор можно вести по каждому из трех каналов связи, соответственно равны 0,75; 0,7; 0,8. Найти вероятность того, что разговор состоится.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [2;4]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
Из 20 имеющихся аппаратов восемь – первого класса, семь – второго, пять – третьего. Вероятности исправной работы для них соответственно равны 0,8; 0,7; 0,5. Найти вероятность того, что случайно выбранный аппарат исправен.
Всхожесть семян кукурузы составляет 98%. Найти вероятность того, что из 5000 посеянных семян не взойдет 2.
Вероятность выигрыша в лотерее на 1 билет равна 0,7. Куплено
11 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,5. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,901 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,01?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,03. Определить вероятность того, что среди 800 поступивших вызовов имеется 5 сбоев.
Вероятность попадания мяча в корзину равна 0,4. Составить закон распределения числа попаданий при трех бросках в корзину. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
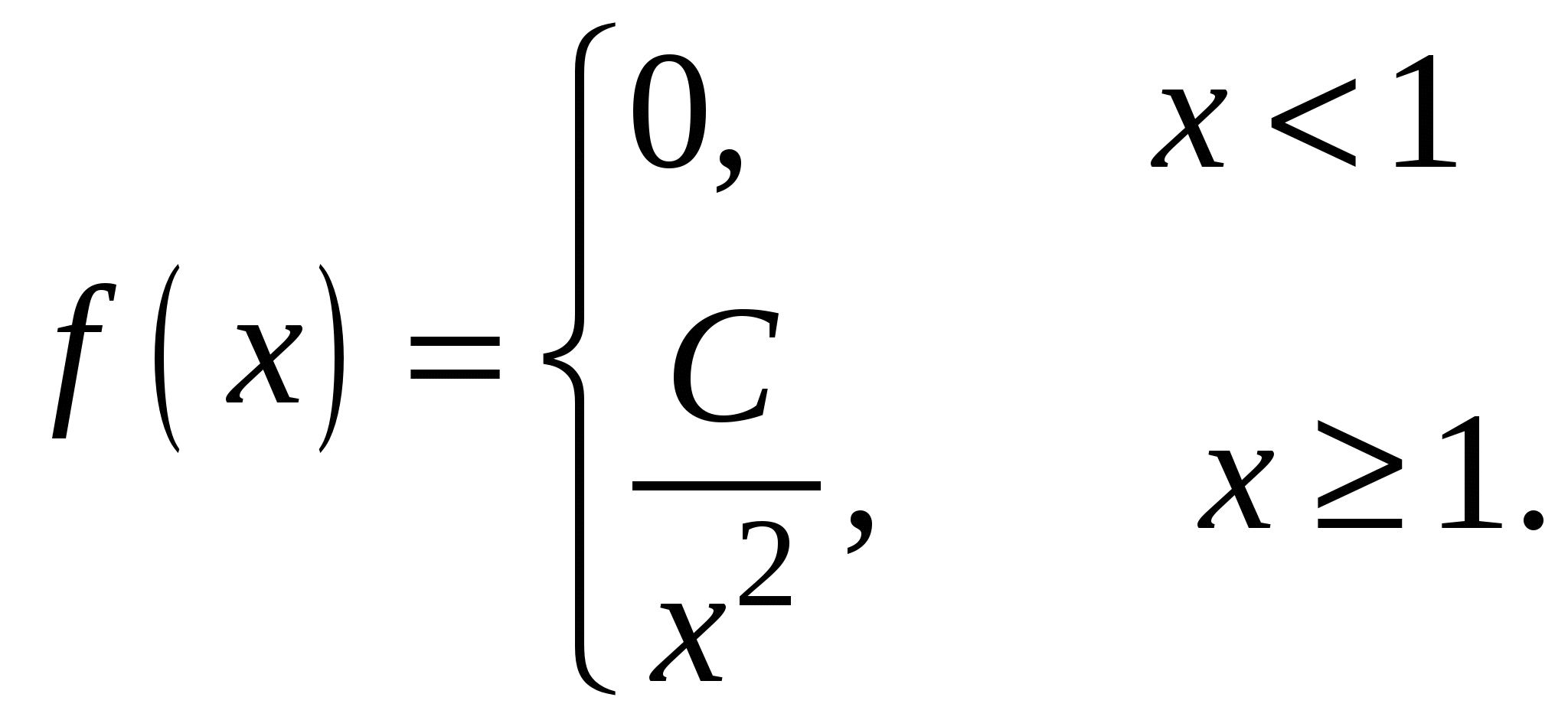
Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (2;5). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2
|
4
|
5
|
6
|
|
У
|
4,3
|
5,1
|
10,6
|
Р
|
0,3
|
0,1
|
0,2
|
0,4
|
|
Р
|
0,2
|
0,3
|
0,5
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0571 отклонится от своего математического ожидания менее, чем на 0,044.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
3
|
6
|
10
|
0,25
|
0,10
|
14
|
0,15
|
0,05
|
18
|
0,32
|
0,013
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.