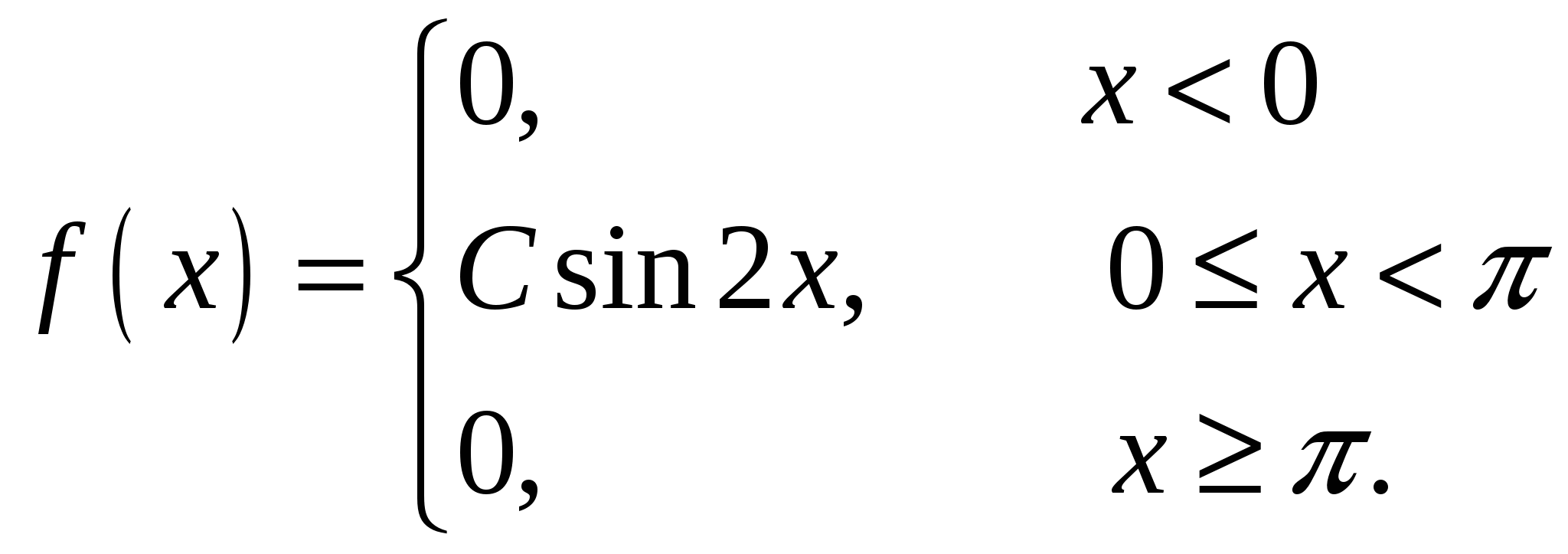Вариант № 26
В течение недели независимо друг от друга происходит 7 различных событий. В один и тот же день может произойти несколько событий и даже все. Сколько различных способов при этом может оказаться? В скольких случаях происходит по одному событию ежедневно?
В замке на общей оси пять дисков. Каждый диск разделен на 6 секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков, замок можно будет открыть.
Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится а) только в одном справочнике; б) хотя бы в одном справочнике.
Наудачу взяты 2 положительных числа Х и У, каждое из которых не превышает 2,5. Найти вероятность того, что произведение ХУ будет не больше двух, а частное У/Х не больше 2,5.
В каждой из двух урн содержится четыре черных и шесть белых шаров. Из второй урны наугад извлечен один шар и положен в первую урну, после чего из первой урны наудачу извлечен шар. Найти вероятность того, что шар, извлеченный из первой урны, окажется белым.
При вытачивании болтов наблюдается в среднем 10% брака. Можно ли быть уверенным, что в партии из 400 болтов окажется пригодным более 299?
Вероятность выигрыша в лотерее на 1 билет равна 0,7. Куплено
10 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,25. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9722 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,01?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,07. Определить вероятность того, что среди 1000 поступивших вызовов имеется 9 сбоев.
Два бомбардировщика бомбят мост. Каждый из них имеет на борту по две бомбы. Вероятность попадания в цель бомб первого бомбардировщика соответственно равны 0,6 и 0,4, а для второго – 0,7 и 0,2. Сначала на цель заходит первый самолет и сбрасывает свою первую бомбу. Если он не попал, на цель заходит второй самолет и сбрасывает свою первую бомбу. Если он не попал – на цель заходит снова первый самолет и т.д., пока не произойдет попадание. Составить закон распределения числа израсходованных бомб. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:
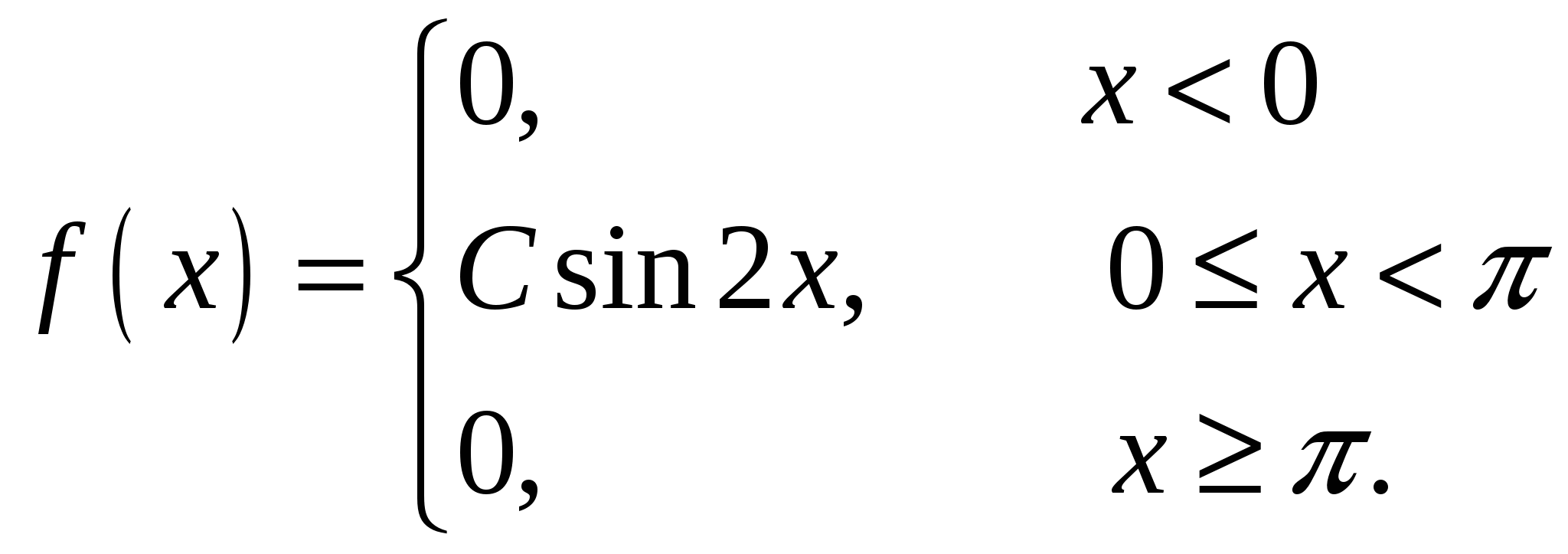
Найти параметр С, функцию распределения случайной величины F(x), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (p/2;3p/4). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
1,1
|
1,2
|
1,3
|
1,4
|
|
У
|
1
|
3
|
5
|
Р
|
0,3
|
0,4
|
0,2
|
0,1
|
|
Р
|
0,4
|
0,3
|
0,3
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,002 отклонится от своего математического ожидания менее, чем на 0,2.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
1
|
2
|
3
|
1,6
|
0,3
|
0,03
|
0,01
|
3,6
|
0,01
|
0,2
|
0,03
|
4,1
|
0,05
|
0,06
|
0,06
|
5,9
|
0,01
|
0,03
|
0,21
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.