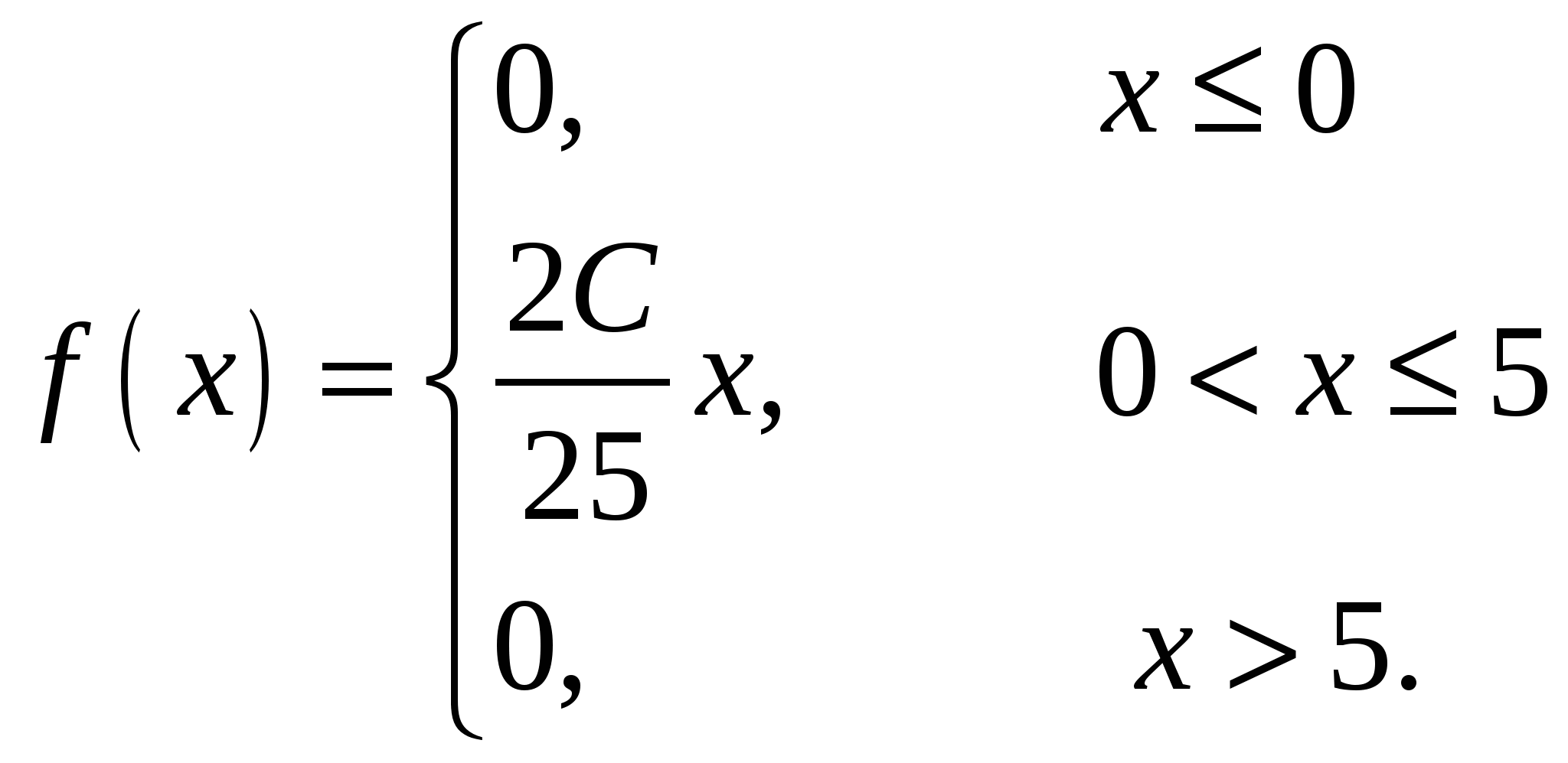Вариант № 22
Среди 17 студентов группы разыгрывается 7 билетов. В группе 8 девушек. В скольких случаях среди обладателей билетов окажутся 4 девушки? Сколько всего способов распределить 7 билетов?
Набирая номер телефона, абонент забыл две последние цифры, помня лишь, что цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить 4 бомбы, вероятности которых равны 0,3; 0,4; 0,6 и 0,7 соответственно.
Наудачу взяты 2 положительных числа Х и У, каждое их них не превышает двух. Найти вероятность того, что произведение ХУ будет не больше 1,5, а сумма Х+У не больше двух.
В 9 одинаковых закрытых урн помещено по 10 шаров, различающихся только по цвету. В две урны положено по 5 белых шаров, в три – по
4 белых шара, и в четыре – по 3 белых шара. Из какой-то урны нажатием кнопки выброшен шар, оказавшийся белым. Найти вероятность того, что эта урна содержит 3 белых шара.
Батарея сделала 14 выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0,2. Найти вероятность разрушения цели, если для этого необходимо не менее 4 попаданий.
Вероятность выигрыша в лотерее на 1 билет равна 0,6. Куплено
10 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,7. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,901 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,02?
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,005. Определить вероятность того, что среди 600 поступивших вызовов имеется 9 сбоев.
В партии из 6 деталей имеется 4 стандартные. Наудачу отобраны 3 детали. Составить закон распределения числа стандартных деталей среди отобранных. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана плотностью распределения:
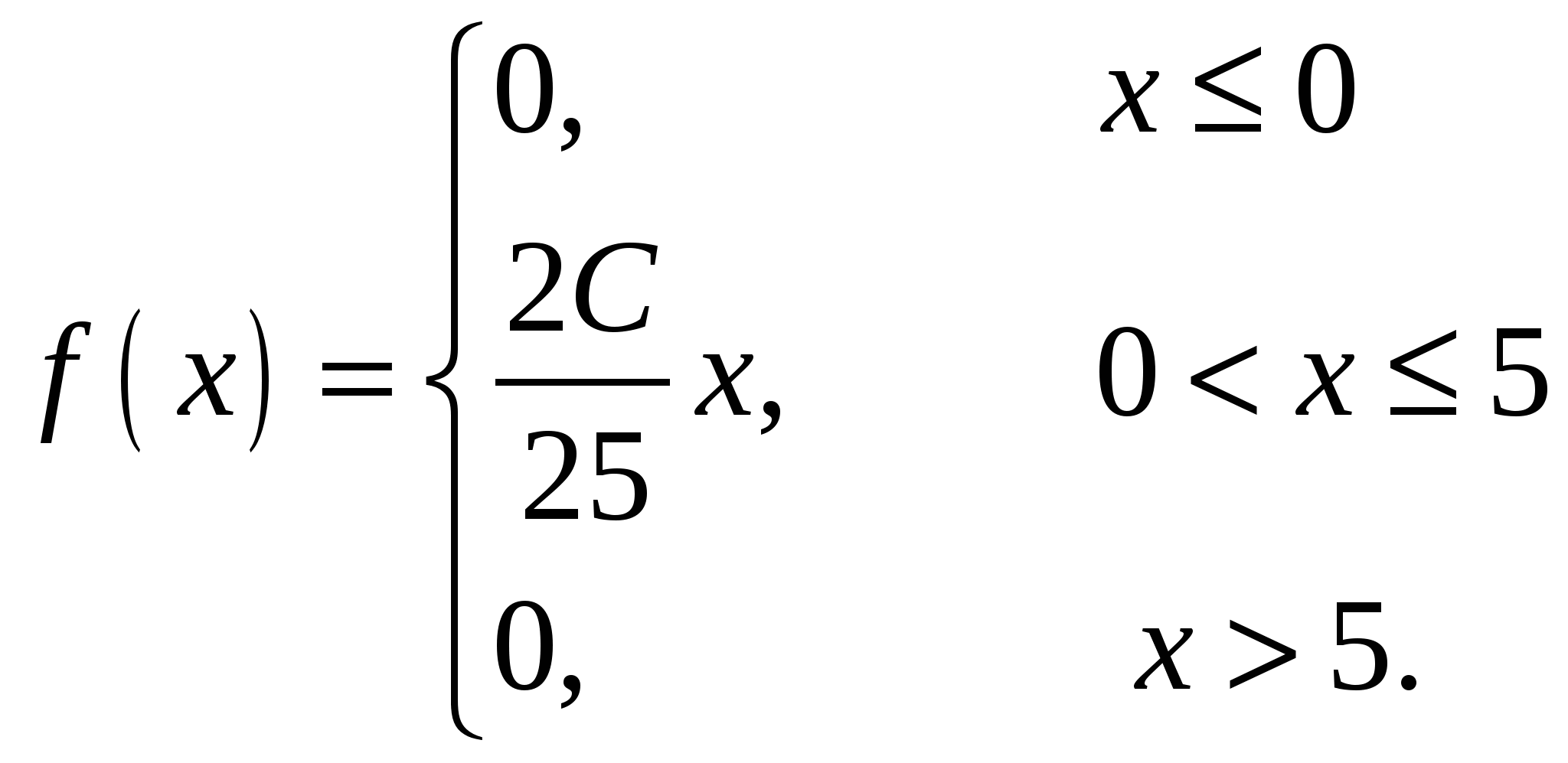
Найти параметр С, функцию распределения F(х) случайной величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (1;3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
1
|
3
|
5
|
7
|
|
У
|
1,2
|
1,6
|
2,0
|
Р
|
0,5
|
0,3
|
0,2
|
0,1
|
|
Р
|
0,6
|
0,3
|
0,1
|
Укажите законы распределения случайной величины Х+У, Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0011 отклонится от математического ожидания менее, чем на 0,1.
Двумерная случайная величина (Х, У) задана таблицей. Найдите её ковариацию коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
2
|
3
|
4
|
3
|
0,03
|
0,01
|
0,01
|
6
|
0,03
|
0,04
|
0,04
|
9
|
0,01
|
0,5
|
0,02
|
10
|
0,01
|
0,03
|
0,27
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.