Вариант № 20
Имеется восемь различных книг. Сколькими способами можно разослать их по одной каждому из восьми различных адресатов? Сколько имеется способов разделить книги на две пачки по четыре книги в каждой?
На каждой из восьми одинаковых карточек написаны числа: 2, 4, 6, 7, 8, 11, 12, 13. Карточки тщательно перемешаны. Наудачу берутся карточки. Найти вероятность того, что образованная из двух выбранных чисел дробь сократима.
Вероятность попадания в цель при залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго эта вероятность равна 0,8.
Наудачу взяты 2 положительных числа Х и У, каждое их них не превышает единицы. Найти вероятность того, что сумма Х+У не превышает единицы, а произведение ХУ не меньше 0,4.
В первом ящике находится 20 деталей, из них 15 стандартных, во втором – 30, из них 24 стандартных, в третьем – 10, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика стандартная.
Вероятность выпуска сверла повышенной хрупкости (брак) равна 0,02. Сверла складываются в коробки по 100 штук. Определить вероятность того, что а) в коробке не окажется бракованных сверл, б) число бракованных сверл не превысит двух.
Вероятность выигрыша в лотерее на 1 билет равна 0,6. Куплено
11 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,3. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,98 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,02?
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,011. Определить вероятность того, что среди 1000 поступивших вызовов имеется 8 сбоев.
Стрелок произвел 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку насчитывается 5 очков. Построить ряд распределения числа выбитых очков и найти математическое ожидание и дисперсию этой случайной величины.
Случайная величина Х задана плотностью распределения:
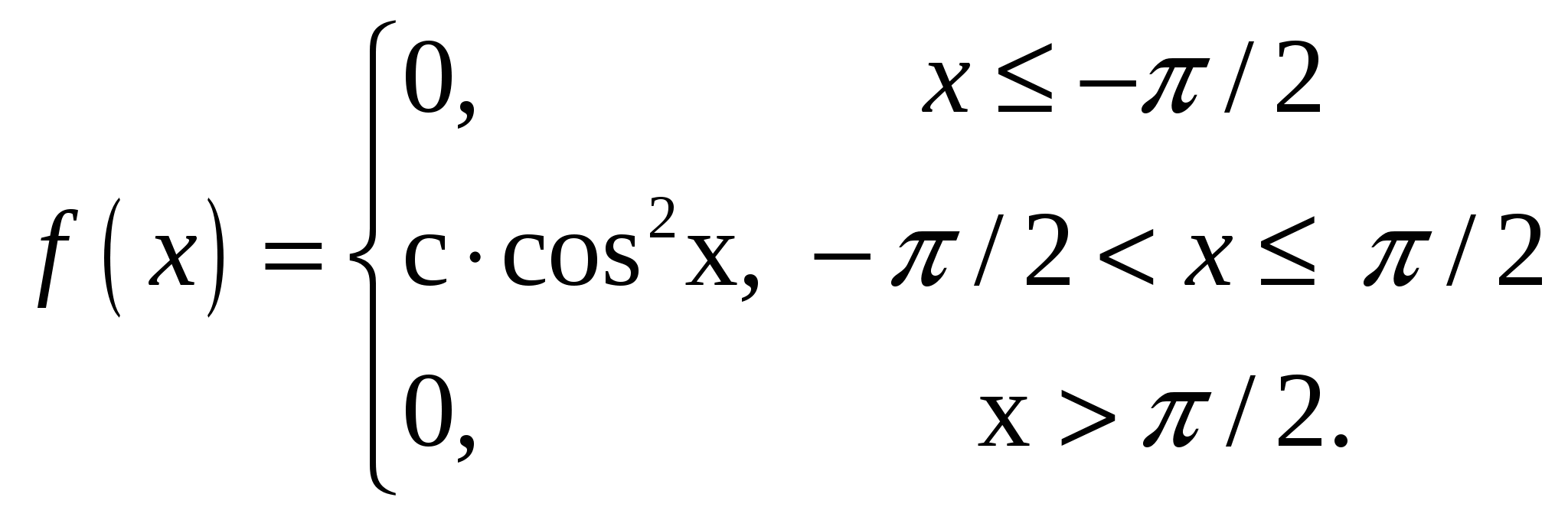
Найти параметр с, функцию распределения F(x) случайной величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (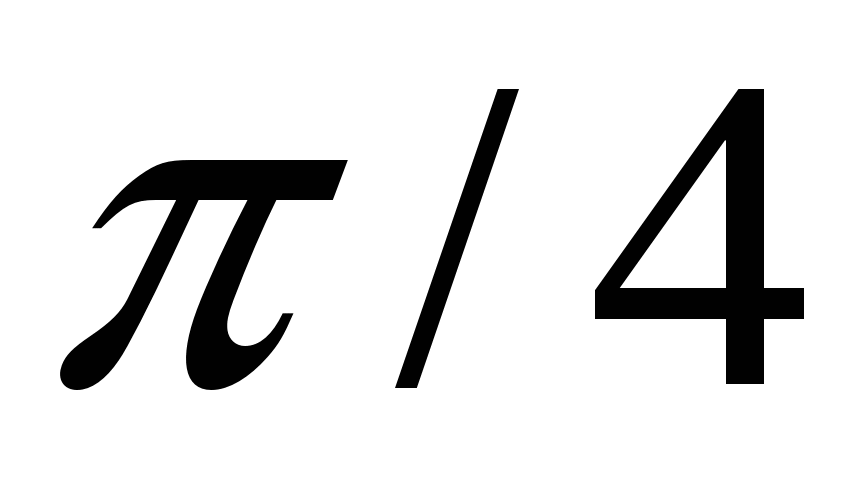 ; ; ). Построить графики функций f(x), F(x). ). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
2,3
|
2,5
|
2,7
|
2,9
|
|
У
|
1
|
2
|
3
|
Р
|
0,4
|
0,3
|
0,2
|
0,1
|
|
Р
|
0,3
|
0,5
|
0,2
|
Укажите законы распределения случайной величины Х+У, Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0162 отклонится от математического ожидания менее, чем на 0,2.
Двумерная случайная величина (Х, У) задана таблицей. Найдите её ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
у х
|
1
|
2
|
3
|
1,5
|
0,03
|
0,02
|
0,02
|
2,9
|
0,06
|
0,13
|
0,03
|
4,1
|
0,4
|
0,07
|
0,02
|
5,6
|
0,15
|
0,06
|
0,01
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.