Вариант № 30
Сколькими различными способами можно переставить буквы между собой: a) А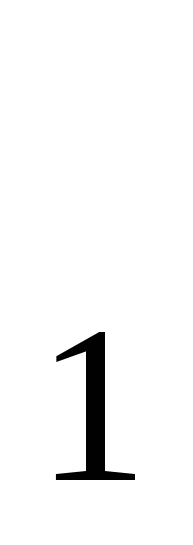 А А В В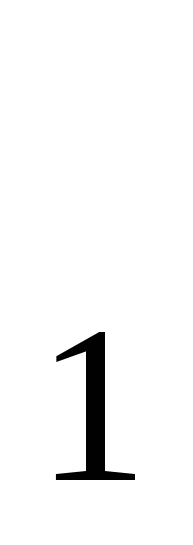 В В В В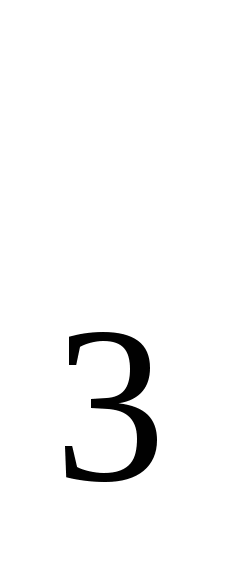 , б) А А В , б) А А В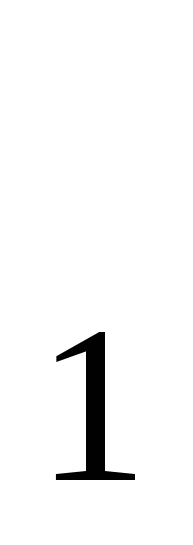 В В В В , в) А А В В В ? , в) А А В В В ?
Среди 25 экзаменационных билетов 5 «хороших». Студент берет два билета. Найти вероятность того, что а) оба они «хорошие», б) среди них один «хороший».
Из орудия производятся два выстрела по некоторому объекту. Вероятность попадания при первом выстреле равна 0,6; при втором – 0,9. Для разрушения объекта достаточно одного попадания. Найти вероятность разрушения объекта.
У квадратного трехчлена х2+px+q коэффициенты p иqвыбраны наудачу из отрезка [1;4]. Какова вероятность того, что квадратный трехчлен имеет действительные корни?
Литье поступает из двух заготовительных цехов: 70% из первого цеха и 30% из второго. При этом материал первого цеха имеет 10% брака, а второго цеха – 5% брака. Найти вероятность того, что взятая наугад болванка без дефектов.
Завод выпускает приборы, среди которых в среднем 98% без дефектов. Найти вероятность того, что в партии из 400 приборов не более четырех дефектных.
Вероятность выигрыша в лотерее на 1 билет равна 0,2. Куплено 12 билетов. Найти наивероятнейшее число выигрышных билетов и соответствующую вероятность.
Вероятность поражения мишени при одном выстреле равна р=0,8. Сколько нужно произвести выстрелов, чтобы с вероятностью 0,9624 отклонение относительной частоты попадания от вероятности р по абсолютной величине не превзошло 0,05?
Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,01. Определить вероятность того, что среди 700 поступивших вызовов имеется 8 сбоев.
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 01. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание, дисперсию этой случайной величины.
Случайная величина Х задана своей плотностью распределения:

Найти параметр С, функцию распределения случайной величины F(х), математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания этой случайной величины в интервал (1;3). Построить графики функций f(x), F(x).
Независимые случайные величины Х и У заданы следующими законами:
Х
|
1
|
3
|
6
|
8
|
|
У
|
-5
|
2
|
3
|
Р
|
0,2
|
0,1
|
0,4
|
0,3
|
|
Р
|
0,4
|
0,4
|
0,2
|
Составьте законы распределения случайных величин Х+У и Х-У и найдите их математическое ожидание и дисперсию.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина с дисперсией 0,0453 отклонится от своего математического ожидания менее, чем на 0,037.
Двумерная дискретная случайная величина (Х,У) задана таблицей. Найти ее ковариацию, коэффициент корреляции и сделать вывод о зависимости случайных величин Х и У.
х у
|
2
|
4
|
6
|
1
|
0,05
|
0,4
|
0,35
|
2
|
0,1
|
0,03
|
0,07
|
|
 Скачать 0.88 Mb.
Скачать 0.88 Mb.
