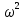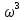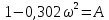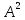тау. ТАУ МУПЗ 28.04.21. Методические указания к практическим занятиям для студентов СанктПетербург 2021 у дк 681 011
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Метод частотных характеристик.Вещественная частотная характеристика U (  ) замкнутой САР однозначно отображает характер переходного процесса. Метод частотных характеристик сводится к разбивке кривой U ( ) замкнутой САР однозначно отображает характер переходного процесса. Метод частотных характеристик сводится к разбивке кривой U ( ) по определенному правилу на треугольники и трапеции. При этом две стороны трапеций будут совпадать с осями координат ) по определенному правилу на треугольники и трапеции. При этом две стороны трапеций будут совпадать с осями координат  и U( и U( ), третья сторона будет параллельна оси ), третья сторона будет параллельна оси , а четвертая — наклонна. Разбиение на трапеции позволяет повысить точность расчета и использовать вспомогательные таблицы. Приняв трапецеидальную форму вещественно-частотной характеристики за типовую и составив таблицы ординат кривых переходного процесса h (t) для единичных трапеций, можно с помощью таблиц и несложных расчетов построить переходные процессы для каждой составляющей вещественно-частотной характеристики. Затем, просуммировав координаты переходных процессов, составляющих характеристики, можно получить переходный процесс для замкнутой САР в целом. , а четвертая — наклонна. Разбиение на трапеции позволяет повысить точность расчета и использовать вспомогательные таблицы. Приняв трапецеидальную форму вещественно-частотной характеристики за типовую и составив таблицы ординат кривых переходного процесса h (t) для единичных трапеций, можно с помощью таблиц и несложных расчетов построить переходные процессы для каждой составляющей вещественно-частотной характеристики. Затем, просуммировав координаты переходных процессов, составляющих характеристики, можно получить переходный процесс для замкнутой САР в целом.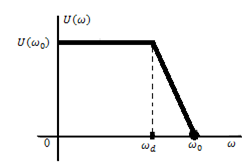 Рис. 6.3 Трапецеидальная вещественная частотная характеристика Трапецеидальная вещественная частотная характеристика (рис. 6.3) определяется высотой U (  ), интервалом пропускания частот ), интервалом пропускания частот 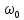 , интервалом равномерного пропускания частот , интервалом равномерного пропускания частот 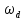 и коэффициентом наклона и коэффициентом наклона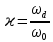 . Для типовой единичной трапеции принимается U ( . Для типовой единичной трапеции принимается U ( ) = 1 и ) = 1 и 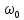 =1. Поэтому единичная трапеция характеризуется только коэффициентом наклона =1. Поэтому единичная трапеция характеризуется только коэффициентом наклона 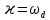 . Для единичных трапеций с различными величинами . Для единичных трапеций с различными величинами 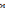 могут быть вычислены ординаты переходного процесса в виде h (t), где t = могут быть вычислены ординаты переходного процесса в виде h (t), где t =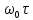 — безразмерный параметр времени. Таким образом, для единичной трапеции t = 1 — безразмерный параметр времени. Таким образом, для единичной трапеции t = 1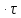 = =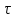 . Величины ординат переходных процессов, вычисленные для различных значений t и . Величины ординат переходных процессов, вычисленные для различных значений t и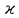 , называются h-функциями. Значения h-функций для трапеций приведены в табл. 6.1. , называются h-функциями. Значения h-функций для трапеций приведены в табл. 6.1.Для перехода от h-функции h (t) к переходной функции х ( 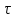 ) соответствующей составляющей трапецеидальной вещественной частотной характеристики с тем же ) соответствующей составляющей трапецеидальной вещественной частотной характеристики с тем же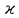 , но с U ( , но с U ( ) )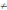 1 и 1 и 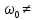 1 необходимо значения h-функций умножить на U ( 1 необходимо значения h-функций умножить на U ( ), а для перехода к действительному значению времени с учетом того, что t = ), а для перехода к действительному значению времени с учетом того, что t =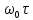 , необходимо, чтобы , необходимо, чтобы 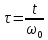 . На основании изложенного . На основании изложенногоx 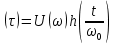 . (6.5) . (6.5)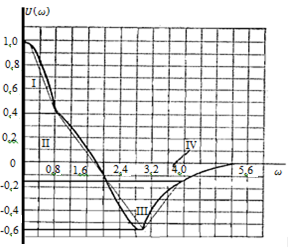 Рис. 6.4 График вещественная частотной характеристики САР Таким образом, порядок построения переходного процесса по методу трапецеидальных частотных характеристик будет следующим: 1) по известным дифференциальным уравнениям САР определяем ее передаточную функцию; 2) в характеристическом уравнении заменяем 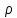 на j на j и находим вещественную частотную характеристику САР; и находим вещественную частотную характеристику САР;3) строим график U (  ) в функции ) в функции  (рис. 6.4); (рис. 6.4);4) фиксируем область U (  ) до существенных частот ) до существенных частот 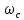 ; ;5) разбиваем U (  ) на треугольники и трапеции; ) на треугольники и трапеции;6) фиксируем параметры треугольников и трапеций U (  ); ); 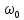 ; ;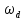 ; ϰ; ; ϰ;7) строим кривые в функции времени 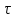 для каждого треугольника и трапеции на основе таблиц h-функций; для каждого треугольника и трапеции на основе таблиц h-функций;8) суммируем ординаты полученных кривых для всех треугольников и трапеций, в результате чего строим кривую x ( 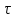 ) для переходного процесса САР в целом при единичном возмущении. ) для переходного процесса САР в целом при единичном возмущении.Рассмотрим построение переходного процесса САР на примере. Допустим, что передаточная функция замкнутой САР имеет вид 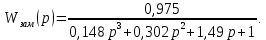 Произведем замену р на j  : :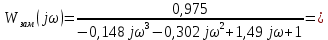 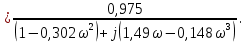 Избавимся от иррациональности в знаменателе: 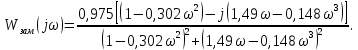 Отсюда вещественная часть будет иметь вид: 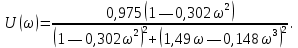 Задаемся значениями  от 0 до ∞ и подставляем их в полученное уравнение, результаты расчетов сводим в табл. 6.1 от 0 до ∞ и подставляем их в полученное уравнение, результаты расчетов сводим в табл. 6.1По данным табл. 6.2 (учитывая, что при  = 0 U = 0 U 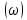 = 0,975) строим вещественную частотную характеристику (рис. 6.4). Разбиваем полученную вещественную характеристику на трапеции, данные для которых сведены в табл. 6.2 = 0,975) строим вещественную частотную характеристику (рис. 6.4). Разбиваем полученную вещественную характеристику на трапеции, данные для которых сведены в табл. 6.2Следует учесть, что сумма высот отдельных трапеций при  = 0 должна соответствовать ординате вещественной характеристики САР при = 0 должна соответствовать ординате вещественной характеристики САР при  = 0, т. е. U( = 0, т. е. U( = 0) = 0,555 + 0,98 — 0,41— 0,15 = = 0,975. = 0) = 0,555 + 0,98 — 0,41— 0,15 = = 0,975.Затем с использованием таблицы h-функций (табл. 6,3) вычисляем значения, на основании которых строим переходные процессы для каждой составляющей вещественной частотной характеристики САР. Данные расчета сведены в табл. 6,4-6.7. Суммировав ординаты переходных процессов составляющих, получим переходный процесс для замкнутой САР в целом (рис. 6,5.) Таблица. 6.1 Расчет прараметров вещественная частотной характеристики 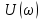
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||