тау. ТАУ МУПЗ 28.04.21. Методические указания к практическим занятиям для студентов СанктПетербург 2021 у дк 681 011
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Амплитудно-фазовый критерий устойчивости НайквистаКритерий устойчивости Найквиста позволяет судить об устойчивости замкнутой линейной системы по виду АФХ той же системы, но в разомкнутом состоянии. Условие устойчивости формулируется следующим образом: если разомкнутая система устойчива, то для обеспечения ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала на комплексной плоскости точку с координатами (— 1, j0). Если же АФХ устойчивой разомкнутой системы охватывает точку с координатами (— 1; j0), то система в замкнутом состоянии будет неустойчивой. АФХ для устойчивой и неустойчивой систем приведены на рис.5.3. 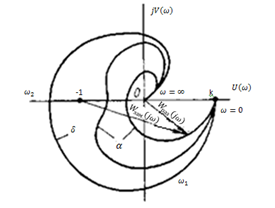 Рис 5.3 АФХ для устойчивой (а) и неустойчивой (б) систем В качестве примера определим устойчивость замкнутой АСР, состоящей из двух звеньев, с помощью критерия Найквиста. В разомкнутом состоянии САР описывается уравнением вида 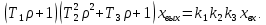 Числовые значения параметров:  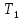 = 2,8 с; = 2,8 с; 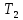 = 0,45 с; = 0,45 с; 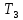 = 3,9 с; = 3,9 с; 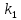 = 3,5; = 3,5;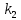 = 2; = 2; 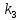 = 3. = 3.Передаточная функция системы будет иметь вид 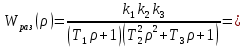 = 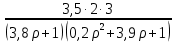 = =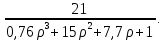 АФХ системы после замены 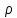 на на 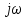 будет иметь вид будет иметь вид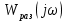 = =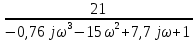 = =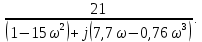 Для того чтобы избавиться от мнимости в знаменателе, необходимо умножить числитель и знаменатель на сопряженный множитель, тогда получим 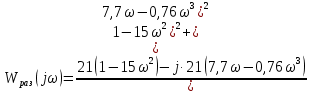 . .Определим вещественную и мнимую части АФХ: 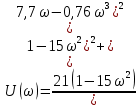 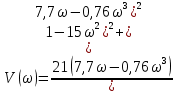 Изменяя  от 0 до от 0 до 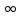 , получим ряд точек, по которым может быть построена на комплексной плоскости АФХ системы. Так как для данного примера построенная АФХ не охватывает точку с координатами (— 1; j0), то система в разомкнутом состоянии будет устойчивой (дальнейший расчет в пособии не приводится). Поскольку САР в разомкнутом состоянии устойчива, то при указанном условии она и в замкнутом состоянии будет устойчива. , получим ряд точек, по которым может быть построена на комплексной плоскости АФХ системы. Так как для данного примера построенная АФХ не охватывает точку с координатами (— 1; j0), то система в разомкнутом состоянии будет устойчивой (дальнейший расчет в пособии не приводится). Поскольку САР в разомкнутом состоянии устойчива, то при указанном условии она и в замкнутом состоянии будет устойчива.Методические указания по выполнению практического заданияРешить задачи: Задача 1 Определить при помощи критерия Михайлова устойчивость САР, уравнение свободного движения которой имеет вид: (а0р3 + а1р2 + а2р + а3)х = 0, где а) а0 = 0,02; а1 = 0,4; а2 = 1,3; а3 = 25 б) а0 = 0,02; а1 = 0,4; а2 = 1,3; а3 = 30 в) а0 = 0,02; а1 = 0,4; а2 = 1,3; а3 = 60 Задача 2 Определить с помощью критерия Михайлова устойчивость САР, если уравнение свободного движения имеет вид: (а0р4 + а1 р3 + а2р2 + а3р + а4)х = 0, где а) а0 = 0,001; а1 = 0,05; а2 = 0,4; а3 = 1; а4 = 20 б) а0 = 0,001; а1 = 0,05; а2 = 0,4; а3 = 1; а4 = 100 Задача 3 Определить устойчивость замкнутой САР с помощью критерия Найквиста, если передаточная функция в разомкнутом состоянии имеет вид: W = K/p(1+T1p)(1+T2p), Где K=86, T1 = 0,02 сек, T2 = 0,03 сек Задание для самостоятельной работы: Определить устойчивость САР частотными методами для САР, заданной в практическом занятии №3 . |
