тау. ТАУ МУПЗ 28.04.21. Методические указания к практическим занятиям для студентов СанктПетербург 2021 у дк 681 011
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Практическое занятие № 4Определение устойчивости САР алгебраическими методами Цель работы состоит в том, чтобы закрепить полученные знания по определению устойчивости САР алгебраическими методами Основные теоретические положения.Одним из основных критериев работоспособности любой САР является ее устойчивость. Под устойчивостью САР понимается свойство системы возвращаться к состоянию установившегося режима после устранения возмущающего воздействия. Устойчивость означает, что колебания, возникшие в системе под воздействием внешних факторов, должны затухать. В неустойчивой системе при приложении к ней внешнего воздействия будут возникать колебания с нарастающей амплитудой, т. е. будет наблюдаться расходящийся процесс. Примером устойчивой системы может быть обыкновенный маятник. При отклонении его из состояния равновесия (внешнее возмущение) через некоторое время он вновь придет в состояние равновесия (рис 4.1а). Примером неустойчивой системы может быть шарик, находящийся на выпуклой поверхности. Если вывести шарик из состояния равновесия, то он уже не вернется в прежнее состояние (рис 4.1б). 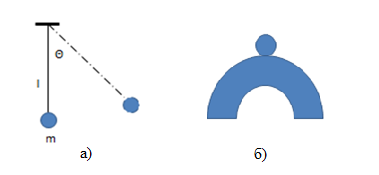 Рис. 4.1 Примеры механических систем: а) устойчивой б) неустойчивой Неустойчивость системы может быть вызвана большой инерционностью элементов САР, малой чувствительностью измерительной аппаратуры и датчиков, неправильной настройкой коэффициентов усиления элементов и другими факторами. В неустойчивой системе выходной параметр будет стремиться к бесконечности, в устойчивой – к нулю. Графики переходных процессов в устойчивой (а) и неустойчивой (б) системах приведены на рис.4.2. 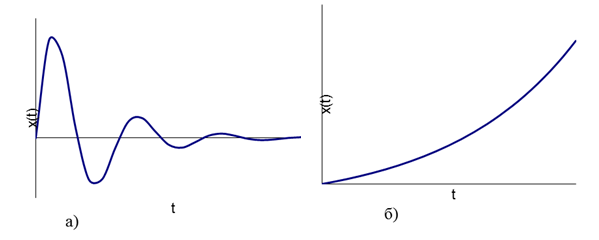 Рис. 4.2 Графики переходных процессов в устойчивой (а) и неустойчивой (б) САР В общем случае динамические свойства САР описываются дифференциальным уравнением n-го порядка, решение которого можно представить суммой двух решений: частного решения, что характеризует установившееся состояние системы, и решения без правой части, что характеризует собственные колебания системы — переходную составляющую процесса регулирования. Собственные колебания системы в операторной форме могут быть описаны однородным уравнением вида 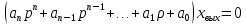 , (4.1), , (4.1),где, 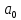 . . . . . .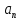 , — постоянные коэффициенты, зависящие от параметров системы. , — постоянные коэффициенты, зависящие от параметров системы.Характеристическое уравнение будет иметь вид 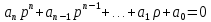 (4.2). (4.2).Уравнение имеет п корней: от 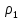 до до 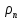 . .Линейная САР будет устойчивой, если все вещественные корни и вещественные части комплексных корней характеристического уравнения будут отрицательны. Неустойчивыми являются все разомкнутые астатические системы, так как их характеристические уравнения имеют сомножителем оператор (р), а следовательно, и нулевые корни. Таким образом, чтобы определить, устойчива или неустойчива САР, достаточно определить корни ее характеристического уравнения. Однако это является сложным, особенно при решении уравнений свыше третьего порядка вручную. Поэтому в теории автоматического регулирования и в инженерной практике широко используются косвенные методы исследования САР на устойчивость, так называемые критерии устойчивости, позволяющие судить об устойчивости динамической системы, не прибегая к вычислению корней характеристического уравнения. Критерий устойчивости И. А. ВышнеградскогоОсновоположник теории автоматического регулирования И. А. Вишнеградский предложил критерий устойчивости, имеющий общее значение для любых динамических систем, описываемых обыкновенным линейным дифференциальным уравнением третьего порядка. 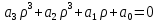 (4.3). (4.3).Для устойчивости линейной системы третьего порядка необходимо и достаточно следующее: а) все коэффициенты характеристического уравнения должны быть положительными б) произведение средних коэффициентов характеристического уравнения должно быть больше произведения крайних коэффициентов, т. е. 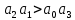 (4.4). (4.4).Границе устойчивости соответствует наличиепары чисто мнимых корней 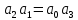 (4.5). (4.5).или наличие нулевого корня 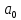 = 0, однако при всех остальных положительных коэффициентах. = 0, однако при всех остальных положительных коэффициентах.Допустим, что передаточная функция замкнутой САР температуры в объекте имеет следующий вид: 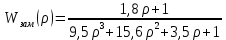 . .Необходимо определить устойчивость системы. Составим характеристическое уравнение 9,5р3+15,6р2 + 3,5р+1=0, где a3>0; a2>0; ах>0; а0>0; А подставив значения в уравнение (4.4) получаем верное неравенство, следовательно: система устойчива. |
