тау. ТАУ МУПЗ 28.04.21. Методические указания к практическим занятиям для студентов СанктПетербург 2021 у дк 681 011
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Практическое занятие № 5Определение устойчивости САР частотными методами Целью работы является закрепление полученных знаний по определению устойчивости САР частотными методами Основные теоретические положения.Графоаналитический частотный критерий устойчивости Л. В. МихайловаДля исследования САР на устойчивость с помощью критерия Михайлова необходимо сначала получить характеристическое уравнение замкнутой системы. Допустим, имеем уравнение вида 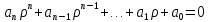 (5.1). (5.1). Затем в характеристическом уравнении производится замена оператора (р) комплексным числом j  . В результате замены будет получена функция комплексного переменного, в которой . В результате замены будет получена функция комплексного переменного, в которой может принимать любые значения от + ∞ до - ∞: может принимать любые значения от + ∞ до - ∞: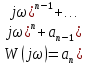 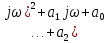 (5.2). (5.2).После этого необходимо выделить мнимую и вещественную части уравнения, учитывая, что 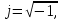 а а 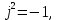 приведя выражение к виду: приведя выражение к виду:W(j  ) = U( ) = U( ) + iV( ) + iV( ) (5.3). ) (5.3).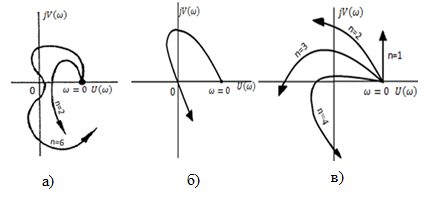 Рис. 5.1 Годограф вектора Михайлова а) неустойчивой САР б) САР на границе устойчивости в) устойчивой САР При изменении частоты  от 0 до ∞ вектор функции комплексного переменного будет поворачиваться против часовой стрелки (т. е. в положительном направлении) около начала координат, изменяя одновременно свою длину. Этот вектор принято называть вектором Михайлова (рисунок 5.1) от 0 до ∞ вектор функции комплексного переменного будет поворачиваться против часовой стрелки (т. е. в положительном направлении) около начала координат, изменяя одновременно свою длину. Этот вектор принято называть вектором Михайлова (рисунок 5.1)Система, описываемая линейным дифференциальным уравнением с постоянными коэффициентами, будет устойчива, если годограф вектора Михайлова при изменении  от 0 до ∞ начинается в точке на положительной вещественной полуоси и последовательно обходит против часовой стрелки п квадрантов и не обращается в нуль, где n — порядок характеристического уравнения системы. от 0 до ∞ начинается в точке на положительной вещественной полуоси и последовательно обходит против часовой стрелки п квадрантов и не обращается в нуль, где n — порядок характеристического уравнения системы.Годографы вектора Михайлова для устойчивых и неустойчивых САР изображены на рис 5.1. Если годограф вектора Михайлова проходит через 0, не заходя в очередной квадрант, то САР на частоте, соответствующей прохождению вектора через 0, находится на границе устойчивости. Рассмотрим в качестве примера определение устойчивости САР температуры в объекте с помощью критерия Михайлова. Допустим, что передаточная функция замкнутой САР имеет вид: 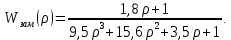 Характеристическое уравнение 9,5р3+15,6р2 + 3,5р + 1=0. Произведем замену в характеристическом уравнении оператора ( 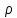 ) комплексным числом j ) комплексным числом j : :W ( 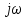 ) = 9,5 ( ) = 9,5 (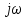 )3 + 15,6 ( )3 + 15,6 (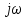 )2 + 3,5 )2 + 3,5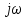 + 1. + 1.Выделим из этого выражения мнимую и вещественную части: U 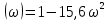 ; ; V 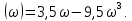 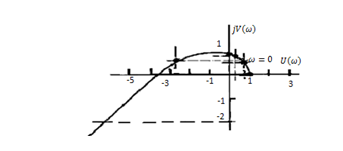 Рис. 5.2 Годограф Михайлова Определим значения мнимой и вещественной частей выражения при различных значениях  (от 0 до ∞). По полученным значениям построим годограф Михайлова (рис. 5.2), откуда видно, что условия устойчивости соблюдены, следовательно, САР устойчива. (от 0 до ∞). По полученным значениям построим годограф Михайлова (рис. 5.2), откуда видно, что условия устойчивости соблюдены, следовательно, САР устойчива. |
