Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
 Скачать 1.23 Mb.
|
|
Пункт 1. Построение поля корреляции результата и фактора производится по исходным данным о парах значений факторного и результативного признаков с соблюдением масштаба. На основе поля корреляции делаются выводы о направлении и возможной функциональной форме связи между факторным и результативным признаками (прямая - обратная, линейная - нелинейная). Д 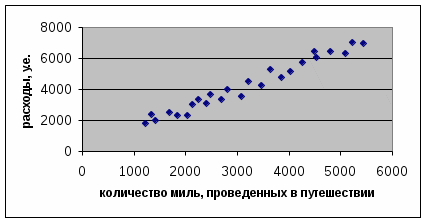 ля условий рассматриваемой задачи поле корреляции выглядит следующим образом: Связь между результативным и факторным признаками прямая, тесная ,линейная, корреляционная. Пункт 2. Оценка параметров уравнения парной линейной регрессии производится обычным методом наименьших квадратов (МНК):  , гдеaиb –оценки параметров модели. Величины, минимизирующие суммы квадратов отклонений 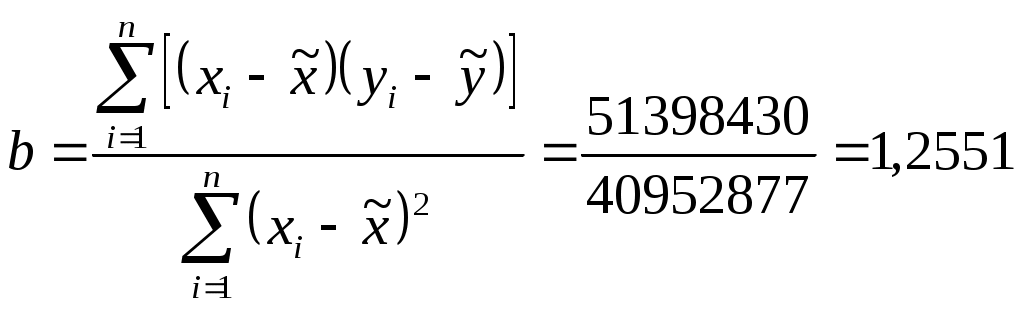 от  для случая парной линейной регрессии, находятся как: ; .Значения ошибок, называемые обычно остатками, рассчитываются как  .Проведите интерпретацию полученных результатов. Расчет необходимых данных лучше всего организовать в таблице. Для нашего примера таблица будет выглядеть следующим образом: Таблица 1
В соответствии с расчетами, представленными в таблице 1, а= 267,7715; b=1,2551 Соответственно уравнение регрессии может быть записано как:  Коэффициент регрессии линейной функции (b) есть абсолютный показатель силы связи, характеризующий среднее абсолютное изменение результата при изменении факторного признака х на единицу своего измерения. Полученное уравнение может быть объяснено следующим образом: с увеличением расстояния на 1 милю расходы путешественника в среднем увеличиваются на 1,2551 условных денежных единиц. Свободный член уравнения равен a=267,7715, что может трактоваться как влияние на величину расходов других, неучтенных в модели факторов. Пункт 3. Парный линейный коэффициент корреляции характеризует тесноту и направление линейной связи между изучаемыми признаками. Его можно определить по следующей формуле:   .Значения линейного коэффициента корреляции принадлежит промежутку [-1;1]. Чем ближе его абсолютное значение к 1, тем теснее связь между признаками. Положительная величина свидетельствует о прямой связи между изучаемыми признаками, отрицательная - о наличии обратной связи между признаками. Для нашей задачи r=0,98329, что подтверждает вывод, сделанный в пункте 1, что связь между признаками прямая, а также указывает на очень сильную взаимосвязь между количеством миль, проведенных в пути и расходами. Квадрат коэффициента (индекса) корреляции называется коэффициентом детерминации и показывает долю вариации результативного признака Y, объясненную вариацией факторного признака X. Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. Например:  =0,8 означает, что доля колеблемости результативного признака, объясненная вариацией фактора  , включенного в уравнение регрессии, составила 80%. Остальные 20% вариации моделируемого показателя объясняются влиянием прочих факторов, не учтенных в уравнении регрессии.Для нашей задачи коэффициент детерминации R2 равен 0,9669, то есть 96,69% вариации результативного признака Y (расходов путешественников) объясняется вариацией факторного признака X(количеством миль, проведенных в пути). Остальные 100% - 96,69%=3,31% вариации Y (расходов путешественников)остались необъясненными в рамках данной модели. Их можно объяснить влиянием прочих факторов, не учтенных в уравнении регрессии. Пункт 4 связан с темой “Проверка статистических гипотез”. Рекомендуется использовать следующую общую процедуру проверки гипотез: 1. Сформулируйте нулевую гипотезу о том, что коэффициент регрессии статистически незначим:  (линейной зависимости между Y и X нет)при конкурирующей:  (линейная зависимость между Y и X есть)или о том, что уравнение в целом статистически незначимо:  . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
