Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
 Скачать 1.23 Mb.
|
|
A – T = S + E. К сожалению, оценки значений тренда, получаемые в результате расчета скользящих средних по 4 точкам, относятся к несколько иным моментам времени, чем фактические данные. Первая оценка, равная 229,75, представляет собой точку, совпадающую с серединой 1996 года, то есть лежит в центре промежутка фактических объемов продаж во II и III кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в III и IV кварталах. Нам же необходимы десезонализированные средние значения, соответствующие тем же интервалам времени, что и фактические значения за квартал. Положение десезонализированных средних во времени сдвигается путем дальнейшего расчета средних для каждой пары значений. Найдем среднюю из первой и второй оценок, центрируя их июнь-сентябрь 1996 года, т.е. (229,75 + 251)/2 = 240,4. Это и есть десезонализированная средняя за июль-сентябрь 1996 г. Эту десезонализированную величину, которая называется центрированной скользящей средней, можно непосредственно сравнивать с фактическим значением за июль-сентябрь 1996 года, равным 182. Отметим, что сглаживание по 4-м точкам приводит к потере оценок тренда за первые два или последние два квартала временного ряда. После расчетов в таблице 2. мы имеем оценки сезонной компоненты, которые включают в себя ошибку или остаток. Прежде чем мы сможем использовать сезонную компоненту, нужно пройти следующие этапы. Шаг 1. Найдем средние значения сезонных оценок для каждого сезона года. Расчеты приведены в таблице 3. Таблица 3. Расчет средних значений сезонной компоненты
Эта процедура позволяет уменьшить некоторые значения ошибок. Наконец, скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы их общая сумма была равна нулю. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год. Обычно корректирующий фактор рассчитывается путем деления суммы оценок сезонных компонент на число сезонов. В нашем же примере оценки второго и третьего кварталов мы округлили до ближайшего большего числа. Значения скорректированной сезонной компоненты подтверждают наши выводы, сделанные на основе диаграммы. Объемы продаж за два зимних месяца превышают среднее трендовое значение приблизительно на 40 тыс. шт., а объемы продаж за два летних месяца ниже средних на 21 и 62 тыс. шт. соответственно. Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Если, например, в качестве сезона выступают дни недели, для элиминирования влияния ежедневной “сезонной компоненты” также рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, то есть в четверг, таким образом, необходимость в центрировании отпадает. Шаг 2 состоит в десезонализации исходных данных. Она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал, то есть A – S = T + E, что показано в таблице 4. Таблица 4 . Расчет десезонализированных данных
Новые оценки тренда, которые все еще содержат ошибку, можно использовать для построения модели основного тренда. Если нанести эти значения на исходную диаграмму, то можно сделать вывод о существовании явного линейного тренда Уравнение линии тренда имеет вид:  ,где х – порядковый номер квартала, а и b – параметры уравнения парной регрессии. Поскольку мы нашли, что тренд имеет линейный характер, то значения параметров линии, аппроксимирующей тренд, найдем методом наименьших квадратов. где y = T + E, 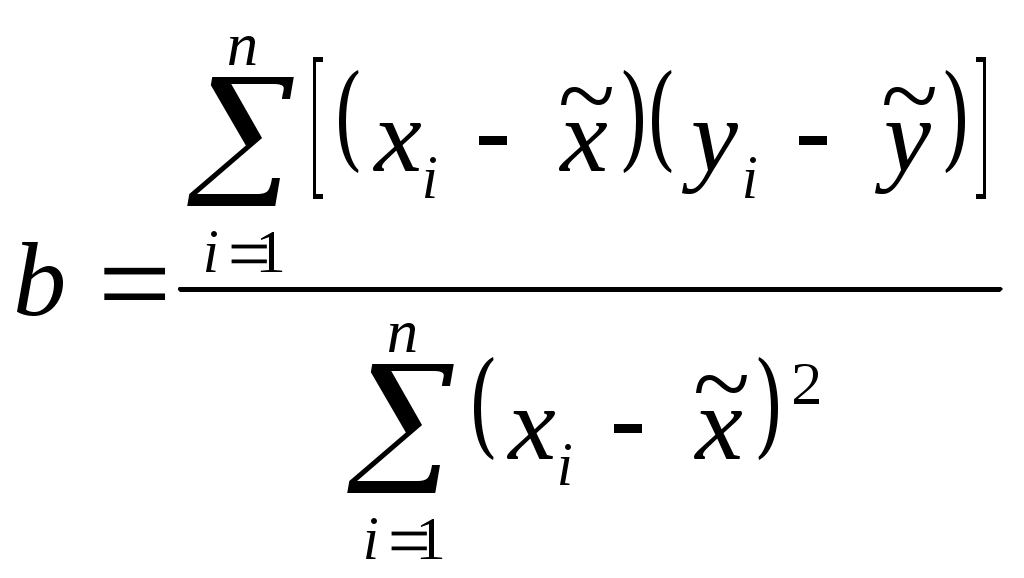 ,  .Подставив значения из последних колонок таблицы 4 в соответствующие формулы, получим:  ,  .Следовательно, уравнение модели тренда имеет следующий вид (с округлением значений коэффициентов регрессии до ближайших целых значений): Трендовое значение объема продаж, тыс. шт. = 180,0 + 20,0 * номер квартала. Шаг 3 нашего алгоритма, предшествующий составлению прогноза состоит в расчете ошибок или остатка. Наша модель имеет следующий вид: A = T + S + E. Значение S было найдено в таблице 2, а значение T в таблице 3. Вычитая каждое значение из фактических объемов продаж, получим значения ошибок. Таблица 5. Расчет ошибок для модели с аддитивной компонентой
Как и в случае линейной регрессии для того, чтобы найти меру соответствия модели исходным данным, необходимо вычислить значения ошибок (остатков) модели, то есть той части значения наблюдения, которую невозможно объяснить с помощью построенной модели. Для этого применяют среднее абсолютное отклонение (mean absolute deviation - MAD) и среднеквадратическую ошибку (mean square error - MCE). Целесообразно использовать обе меры, так как последняя их этих мер резко возрастает при наличии высоких ошибок. Мы можем использовать в шаге 4 последний столбец таблицы 5 для расчета MAD и MSE.  ;  В нашем случае ошибки достаточно малы и составляют от 1 до 3% от уровней ряда. Тенденция, выявленная по фактическим данным, достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы. Прогнозные значения по модели с аддитивной компонентой рассчитывают как: F=T+S (тыс. шт. за квартал), где трендовое значение Т=180+20номер квартала, а сезонная компонента S составляет +42,6 в январе-марте, -20,7 в апреле-июне, 62,0 в июле-сентябре и +40,1 в октябре-декабре. Порядковый номер квартала, охватывающего ближайшие три месяца с апреля по июль 1999 г., равен 14, таким образом, прогнозное трендовое значение составит: Т14=180+2014=460 (тыс. шт. за квартал). Соответствующая сезонная компонента равна –20,7 тыс. шт. Следовательно, прогноз на этот квартал определяется как: F (апрель-июнь 1999г.)=460-20,7=439,3 тыс. шт. Не следует забывать: чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза. В данном случае мы предполагаем, что тенденция, обнаруженная по ретроспективным данным, распространяется и на будущий период. Для сравнительно небольших периодов упреждения такая предпосылка может действительно иметь место, однако ее выполнение становится менее вероятным по мере сопоставления прогнозов на более отдаленную перспективу. Рассмотрим практическую реализацию методики решения задачи для модели с мультипликативной компонентной. В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения. Таким образом, значения сезонной компоненты увеличиваются с возрастанием значений тренда. Пример 2. Компания LORALtd осуществляет реализацию нескольких видов продукции. Объемы продаж одного из продуктов за последние 13 кварталов представлены в таблице 6. Таблица 6. Квартальные объемы продаж компании LORA Ltd
Построим график, позволяющий сделать выводы о типе модели: 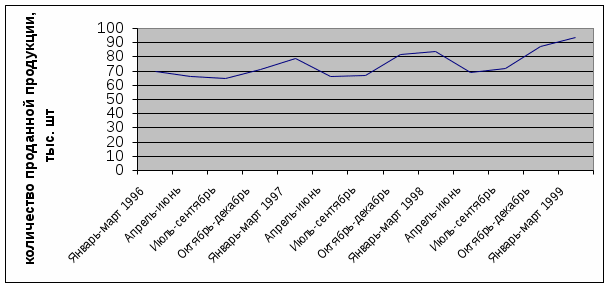 Объем продаж этого продукта так же, как и в предыдущем примере, подвержен сезонным колебаниям, и значения его в зимний период выше, чем в летний. Однако размах вариации фактических значений относительно линии тренда постоянно возрастает. К таким данным следует применять модель с мультипликативной компонентной: Фактическое значение = Трендовое значение  Сезонная вариация Ошибка,т.е. А = T S EВ нашем примере есть все основания предположить существование линейного тренда, но чтобы полностью в этом убедиться, проведем процедуру сглаживания временного ряда. В сущности эта процедура ничем не отличается от той, которая применялась для аддитивной модели. Так же вычисляются центрированные скользящие средние для трендовых значений, однако оценки сезонной компоненты представляют собой коэффициенты, полученные по формуле А/Т= S E. Результаты расчетов приведены в табл. 7.Таблица 7. Расчет значений сезонной компоненты для LORA Ltd
Значения сезонных коэффициентов получены на основе квартальных оценок по аналогии с алгоритмом, который применялся для аддитивной модели. Так как значения сезонной компоненты - это коэффициенты, а число сезонов равно четырем, необходимо, чтобы их сумма была равна четырем, а не нулю, как в предыдущем случае. (Если бы в исходных данных предполагалось семь сезонов в течение недели по одному дню каждый, то общая сумма значений сезонной компоненты должна была бы равняться семи). Если эта сумма не равна четырем, производится корректировка значений сезонной компоненты точно таким же образом, как это уже делалось ранее. В таблице оценки, рассчитанные в последнем столбце предшествующей табл. 8, расположены под соответствующим номером квартала. Таблица 8.Расчет значений сезонной компоненты для LORA Ltd
Как показывают оценки, в результате сезонных воздействий объемы продаж в январе-марте увеличиваются на 11,6 % соответствующего значения тренда (1,116). Аналогично сезонные воздействия в октябре-декабре приводят к увеличению объема продаж на 5,5 % от соответствующего значения тренда. В двух других кварталах сезонные воздействия состоят в снижении объемов продаж, которое составляет 90,7 и 92,2 % от соответствующих трендовых значений. После того, как оценки сезонной компоненты определены, можем приступить к процедуре десезонализации по формуле А/S= T E. Результаты расчетов этих оценок значений тренда приведены в табл. 9.Таблица 9. Расчет уравнения тренда для компании LORA Ltd
Теперь нужно принять решение о том, какой вид будет иметь уравнение тренда. Очевидно, что линия тренда - не кривая, наоборот, она несколько больше напоминает прямую, хотя отдельные точки, особенно значения за 1996 г, расположены хаотически. Предположим для простоты, что тренд линейный, и для расчета параметров прямой, наилучшим образом его аппроксимирующей, будем применять метод наименьших квадратов, который дает следующий результат: Т = 64,6 + 1,36 номер квартала (тыс. шт. в квартал).Это уравнение будем использовать в дальнейшем для расчета оценок трендовых объемов продаж на каждый момент времени. Итак, мы нашли значения тренда и сезонной компоненты. Теперь мы можем использовать их для того, чтобы рассчитать ошибки в прогнозируемых по модели объемах продаж Т Sпо сравнению с фактическими значениями А. В табл.10 эти ошибки рассчитаны как отношение Е = А/(Т S).Для каждого года ошибки достаточно велики, что видно из графика десезонализированных значений. Однако, начиная и первого квартала 1997 г., величина ошибки составляет в среднем 2-3 % от фактического значения, и можно сделать вывод о соответствии построенной модели фактическим данным. Таблица 10.Расчет ошибок для компоненты LORALtd.
При составлении прогнозов по любой модели предполагается, что можно найти уравнение, удовлетворительно описывающее значение тренда. В обоих изложенных выше примерах эти предпосылка была успешно выполнена. Тренд, который нами рассматривался, был очевидно линейный. Если бы исследуемый тренд представлял собой кривую, мы были бы вынуждены моделировать эту связь с помощью одного из методов формализации нелинейных взаимосвязей, рассмотренных в предыдущей главе. После того, как параметры уравнения тренда определены, процедура составления прогнозов становится совершенно очевидной. Прогнозные значения определяются по формуле: F= Т S,где Т=64,6+1,36 номер квартала (тыс. шт. за квартал),а сезонные компоненты составляют 1,116 в первом квартале, 1,097 - во втором, 0,922 - в третьем и 1,055 в четвертом квартале. Ближайший следующий квартал - это второй квартал 1999г., охватывающий период с апреля по июнь и имеющий во временном ряду порядковый номер 14. Прогноз объема продаж в этом квартале составляет: F= Т S = (64 + 1,36 14) 0,907 = 83,64 0,907 = 75,9 (тыс. шт. за квартал).С учетом величины ошибки прогноза мы можем сделать вывод, что данная оценка будет отклоняться от фактического значения не более, чем на 2 - 3 %. Аналогично, прогноз на октябрь-декабрь 1999 г., рассчитывается для квартала с порядковым номером 16 с использованием значения сезонной компоненты для IV квартала года: F = Т S = (64 + 1,36 16) 1,055 = 83,36 1,055 = 91,1(тыс. шт. за квартал).Разумно предположить, что величина ошибки данного прогноза будет несколько выше, чем предыдущего, поскольку этот прогноз рассчитан на более длительную перспективу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2
E