Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
 Скачать 1.23 Mb.
|
|
2. Определите фактическое значение соответствующего критерия. 3. Сравните полученное фактическое значение с табличным. 4. Если фактическое значение используемого критерия превышает табличное, нулевая гипотеза отклоняется, и с вероятностью (1-  ) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если фактическое значение t - критерия меньше табличного, оснований отклонять нулевую гипотезу - нет.Статистическая значимость коэффициента регрессии  проверяется с помощью t - критерия Стьюдента: ,где Sb –это стандартная ошибка коэффициента регрессии: 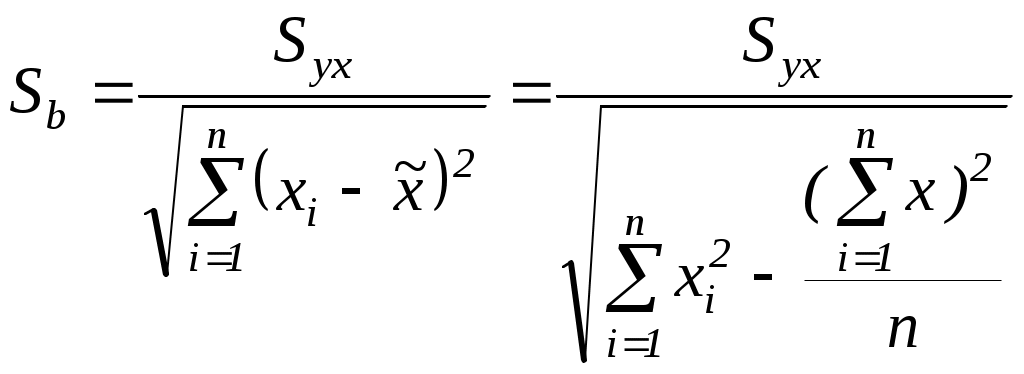 , 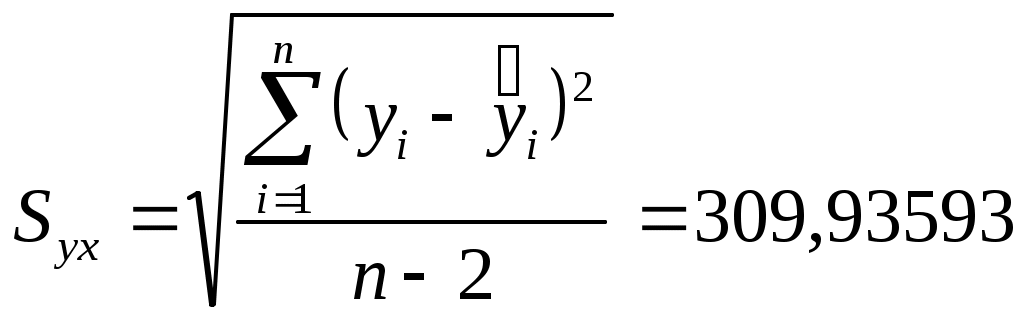- стандартная ошибка оценки уравнения, рассчитываемая по формуле: .Так как нулевая гипотеза предполагает, что =0, то tнабл. рассчитывается как: .Для определения табличного значения воспользуйтесь таблицами распределения Стьюдента для заданного уровня значимости α, принимая во внимание, что число степеней свободы для распределения Стьюдента равно (k = n - 2). Для нашего примера  , >  =2,07, следовательно, нулевая гипотеза отвергается в пользу альтернативной и коэффициент регрессии статистически значим, то есть наличие существенной линейной зависимости между количеством миль, проведенных в путешествии (Х) и величиной расходов(Y) статистически подтверждается.Оценка статистической значимости построенной модели регрессии в целом производится с помощью F- критерия Фишера. Фактическое значение F-критерия, который представляет собой отношение объясненной суммы квадратов SSR (в расчете на одну независимую переменную) к остаточной сумме квадратов SSE (в расчете на одну степень свободы), определяется как: 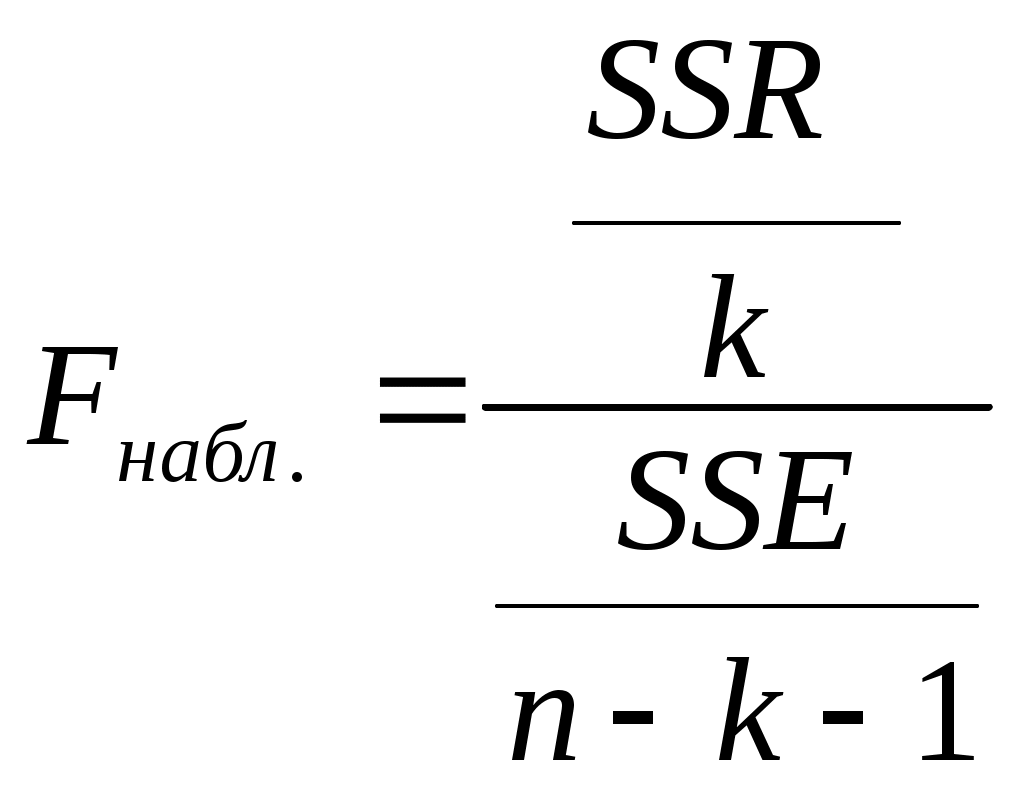 ,где SSR =  - факторная, или объясненная моделью регрессии, сумма квадратов,  - остаточная, или необъясненная моделью сумма квадратовk - число независимых переменных. F - критерий можно также выразить через коэффициент детерминации: 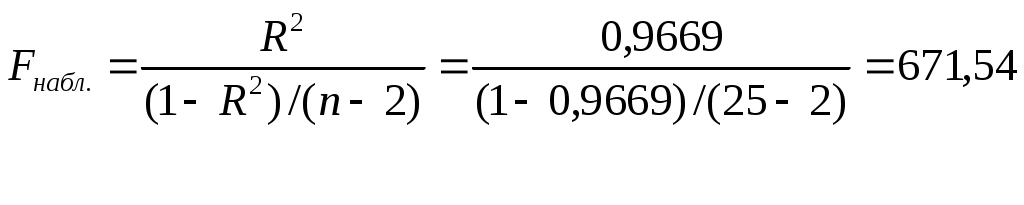 .Для определения табличного значения необходимо воспользоваться таблицами распределения Фишера-Снедекора для заданного уровня значимости α, принимая во внимание, что в случае парной регрессии число степеней свободы большей дисперсии (к1) равно 1, а число степеней свободы меньшей дисперсии (к2) равно n - 2. Для нашего примера  =671,54, а  =4,45. Так как  , то построенная модель регрессии в целом значима и может в дальнейшем использоваться для прогнозов.Пункт 5. Для выполнения пункта 5 необходимо изучить вопрос об интервальном оценивании в регрессионном анализе, уяснить смысл понятий “точечный прогноз” и “интервальный прогноз”. Для нахождения точечного прогноза  необходимо подставить в уравнение регрессии заданное значение факторного признака  . Так, например, если необходимо оценить расходы путешественника, собирающегося преодолеть 4500 миль(x*), следует использовать уравнение регрессии, записанное в пункте 2:  , то есть путешественник, который преодолеет 4500 миль, израсходует 5915,7215 условных денежных единиц. Это значение называется точечным прогнозом.Для нахождения интервального прогноза строятся следующие доверительные интервалы: Доверительный интервал для значений 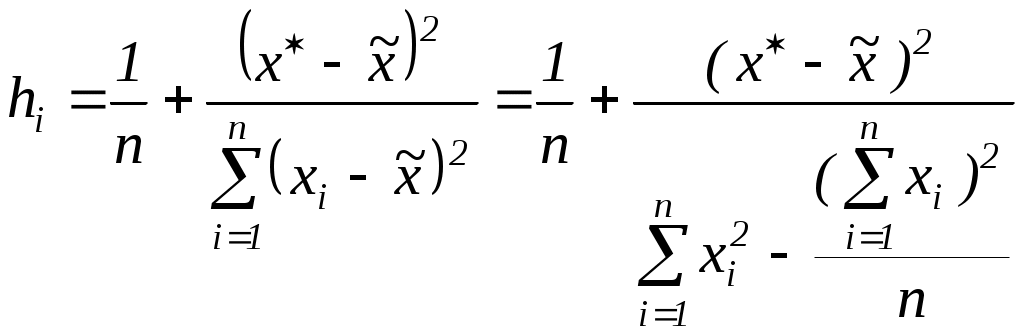 , лежащих на линии регрессии, имеет вид: ,где  - прогнозное значение зависимой переменной; - стандартная ошибка оценки уравнения;n – объем выборки;  - заданное значение факторного признака  .Полученный интервал будет характеризовать значения результативного признака при заданном значении факторного признака  для отдельной наблюдаемой единицы. Так, для нашего примера этот доверительный интервал будет выглядеть как P(5247,8367  6582,9665)=0,95, то есть с доверительной вероятностью 0,95 можно утверждать, что расходы каждого путешественника в генеральной совокупности, преодолевшего 4500 миль, составят от 5247,8367 до 6582,9665 условных денежных единиц.Если же необходимо сделать вывод об интервале средних значений результативного признака Y для всех наблюдаемых единиц (для генеральной совокупности) при заданном значении факторного признака , расчет будет производиться по формуле доверительного интервала для оценки генерального среднего значения  : В соответствии с условиями рассматриваемого примера доверительный интервал, характеризующий средние расходывсех путешественников, преодолевших 4500 миль будет выглядеть как P(5730,918  6099,885)=0,95, то есть с доверительной вероятностью 0,95 можно утверждать, что средние расходывсех путешественников в генеральной совокупности , преодолевших расстояние в 4500 миль будут находиться в границах от 5730,918 до 6099,885 условных денежных единиц.Задача 2 составлена по теме “Множественная регрессия и корреляция” и предполагает построение и анализ двухфакторного уравнения множественной линейной регрессии вида:  .Рассмотрим методику решения задачи такого типа на примере: Компания, производящая моющие средства, предприняла рекламную акцию в магазинах с демонстрацией антисептических свойств нового моющего средства. В этот же период компания использовала обычную теле- и радиорекламу. Через 10 недель компания решила проанализировать сравнительную эффективность различных видов рекламных расходов. Аналитик компании, исходя из гипотезы о линейной регрессионной взаимосвязи, оценил параметры модели следующего вида:  ,где  – объем продаж моющего средства (у.е.), – расходы на теле и радио рекламу (у.е.), – расходы на демонстрацию товара в магазинах (у.е.).Расходы приведены в условных денежных единицах. Таблица 1. Исходные данные
Пункт 1 посвящен анализу показателей тесноты связи в уравнении множественной регрессии. Прежде чем приступить к анализу показателей тесноты связи необходимо рассмотреть дискриптивные (описательные статистики), которые подробно изучались в курсах математической статистики с элементами теории вероятностей и теории статистики. Таблица 2. Дискриптивные (описательные) статистики
Сравнивая значения средних величин и стандартных отклонений, находим коэффициент вариации, значения которого свидетельствуют о том, что уровень варьирования признаков находится в допустимых пределах (< 0,35). Значения коэффициентов асимметрии и эксцесса указывают на отсутствие значимой скошенности и остро-(плоско-) вершинности фактического распределения признаков по сравнению с их нормальным распределением.1 По результатам анализа дискриптивных статистик можно сделать вывод, что совокупность признаков – однородна, то есть для её изучения можно использовать метод наименьших квадратов (МНК) и вероятностные методы оценки статистических гипотез. Парный коэффициент корреляции - это линейный коэффициент корреляции, характеризующий степень тесноты и направление линейной связи между результативным и факторным признаками. Методика его расчета и интерпретация была изложена в пункте 3 задачи 1. При выполнении задания необходимо выписать матрицу парных коэффициентов корреляции. Значения линейных коэффициентов парной корреляции представлены в матрице парных коэффициентов (таблица 3). Они определяют тесноту парных зависимостей между анализируемыми переменными. Таблица 3.Парные коэффициенты линейной корреляции Пирсона:
Коэффициент корреляции ryx1=0,9393 свидетельствует об очень тесной прямой связи между объемом продаж моющего средства и расходами на радио и теле рекламу: увеличение расходов на рекламу увеличивает объем продаж. Коэффициент корреляции ryx2=0,4167 свидетельствует о прямой слабой связи между объемом продаж и расходами на демонстрацию товара в магазинах. Коэффициент корреляции rx1x2=0,4174 свидетельствует о слабой прямой связи между факторами. Таким образом, можно сделать предварительное заключение о том, что расходы на демонстрацию моющего средства в магазинах, существенно не влияют на рост объема продаж нового моющего средства. Частные коэффициенты корреляции характеризуют тесноту связи между результативным и факторным признаками при фиксированном воздействии других факторов, включенных в уравнение регрессии. Их можно определить, используя парные коэффициенты корреляции по следующим формулам: 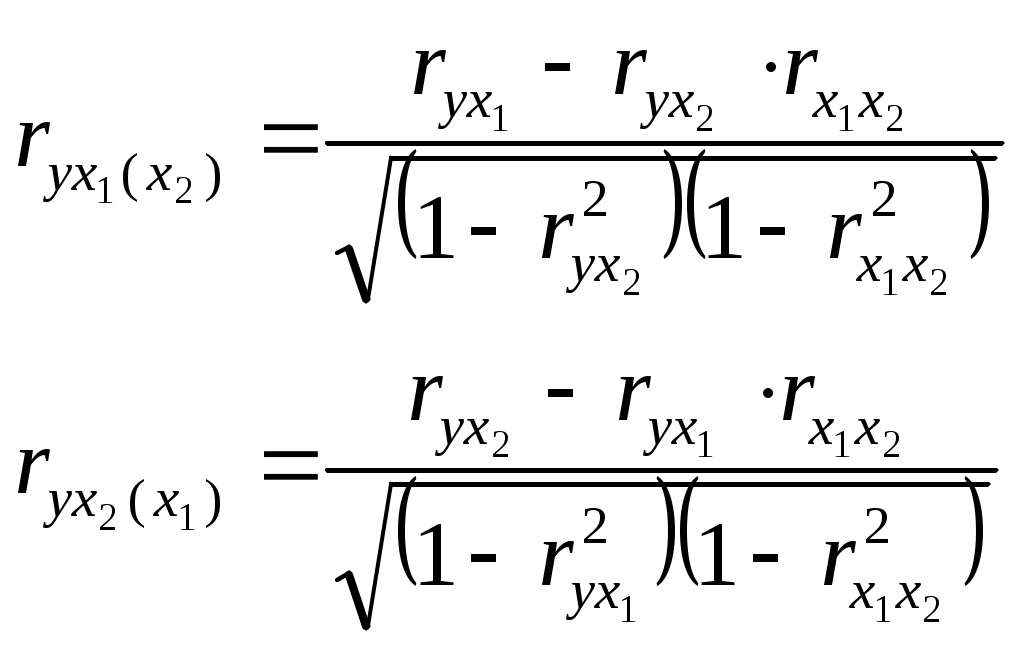 ,где  - частный коэффициент корреляции между результативным и первым факторным признаками при фиксированном воздействии второго факторного признака, - частный коэффициент корреляции между результативным и вторым факторным признаками при фиксированном воздействии первого факторного признака, ,  ,  - парные коэффициенты корреляции.Интерпретируйте полученные значения частных коэффициентов корреляции и поясните причины различий между значениями частных и парных коэффициентов корреляции. Приведенные в таблице 4 линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии. Таблица 4. Частные коэффициенты корреляции
Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как «очищают» парную зависимость от взаимодействия данной пары переменных с другими переменными, представленными в модели. Наиболее тесно связаны и ,  . Другие взаимосвязи существенно слабее. При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между и происходит некоторое завышение оценки тесноты связи между переменными. Пункт 2. Расчет параметров линейного уравнения множественной регрессии осуществляется обычным МНК путем решения системы нормальных уравнений. Для уравнения с двумя объясняющими переменными система примет вид: 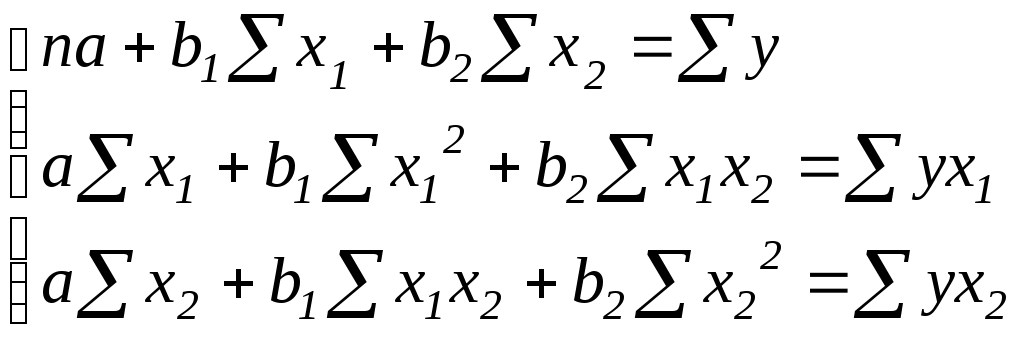 Поясним экономический смысл коэффициентов регрессии  и  : это показатели, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака y при изменении факторного признака на единицу своего измерения при фиксированном влиянии второго фактора.Результаты построения уравнения множественной регрессии представлены в таблице 5. Таблица 5. Результаты построения модели множественной регрессии: Таблица 5.
Уравнение множественной принимает следующий вид: y = 44,61 + 2,35x1 + 0,16x2 Значения стандартных ошибок параметров представлены в графе 3 таблицы 5:  Их значения используются для расчета t-критерия Стьюдента (графа 4): 9,73;  =6,51;  =0,21; tкр.(0,05;7) = 2,36tкр.(0,05;n-3) В нашем примере коэффициент регрессии  является статистически значимым, а коэффициент регрессии  - нет.2 На это же указывает значение вероятности случайных значений параметров регрессии (графа 5), если вероятность меньше принятого за стандарт уровня = 0,05, то делается вывод о неслучайной природе данного значения параметра, то есть о том, что он статистически значим и надежен. В противном случае принимается нулевая гипотеза (H0) о случайной природе значения коэффициентов уравнения. В нашем примере для переменной х2 > 0,05 (х2=0,84), что свидетельствует о незначимости этой переменной. Интерпретация коэффициентов регрессии в построенной модели: Коэффициент регрессии  =2,35 показывает, что с увеличением расходов на теле-радио рекламу.(x1) на 1 у.е. объем продаж нового моющего средства (y) возрастет в среднем на 2,35у.е. при неизменных средних расходах на демонстрацию товара в магазинах (x2). Коэффициент регрессии  =0,16 показывает, что увеличение расходов на демонстрацию товара в магазинах приводит к увеличению объема продаж товара в среднем на 0,16у.е. при неизменных средних расходах на теле-радиорекламу нового моющего средства (x1).Константа уравнения a = 44,61 отражает агрегированное влияние прочих факторов, не включенных в данную модель. Пункт 3 связан с расчетом и анализом относительных показателей силы связи в уравнении множественной регрессии - частных коэффициентов эластичности. Частные коэффициенты эластичности рассчитывают для средних значений факторного и результативного признака:  ,  где  - коэффициент регрессии при j-м факторе, - среднее значение j-го факторного признака;  - среднее значение результативного признака, m - число факторных признаков в уравнении множественной регрессии. Зачастую интерпретация результатов регрессии более наглядна, если произведен расчет частных коэффициентов эластичности. Частные коэффициенты эластичности  показывают, на сколько процентов от значения своей средней  изменяется результат(y) при изменении фактора xj на 1% от своей средней  и при фиксированном воздействии на y прочих факторов, включенных в уравнение регрессии. В нашем примере:  По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат (объем продаж моющего средства) рекламной компании по радио и телевидению, нежели демонстрации товара в магазинах. Пункт 4 предполагает оценку совокупного влияния факторных признаков на результативный признак. Необходимо оценить долю вариации результативного признака (y), объясненную совокупным влиянием факторных признаков, рассчитав совокупный множественный коэффициент детерминации  : , где SSR= - факторная, или объясненная моделью регрессии, сумма квадратов отклонений, SST =  - общая сумма квадратов отклонений,  - остаточная, или не объясненная моделью регрессии сумма квадратов отклонений.В нашем примере  = 88,29% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, т.е. 88,29% вариации объемов продаж можно объяснить вариацией расходов на теле-радио рекламу и вариацией расходов на демонстрацию товара в магазинах. Остальные 11,71% (100% - 88,29%) вариации моделируемого показателя остались не объясненными в рамках данной модели. их можно отнести на влияние прочих факторов, не включенных в данную модель.
Скорректированный множественный коэффициент детерминации  = 0,849(где n – число наблюдений, m – число объясняющих переменных) определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую детерминированность результата y в модели факторами x1 и x2. Оценим степень тесноты связи между результативным признаком и всеми факторными, включенными в уравнение регрессии, определив совокупный множественный коэффициент корреляции:  = 0,9396, то есть между объемом продаж, затратами на теле-радио рекламу и затратами на демонстрацию нового товара в магазинах имеет место очень тесная корреляционная связь.Пункт 5 предполагает ознакомление с методикой дисперсионного анализа по модели множественной регрессии. Проверьте статистическую значимость всей модели регрессии в целом с помощью F-критерия Фишера. Для этого воспользуйтесь алгоритмом проверки гипотез, изложенном в указаниях к пункту 4 задачи 1, учитывая, что фактическое значение F – критерия для уравнения множественной регрессии определяется по формуле:  ,где k - общее число параметров в уравнении множественной регрессии (в случае двухфакторной линейной регрессии k = 3). Для проведения дисперсионного анализа и расчета фактического значения F - критерия рекомендуется также заполнить таблицу результатов дисперсионного анализа:
Для нашего примера: Таблица 6. Дисперсионный анализ модели множественной регрессии
Оценку надежности уравнения регрессии в целом, его параметров и показателя тесноты связи 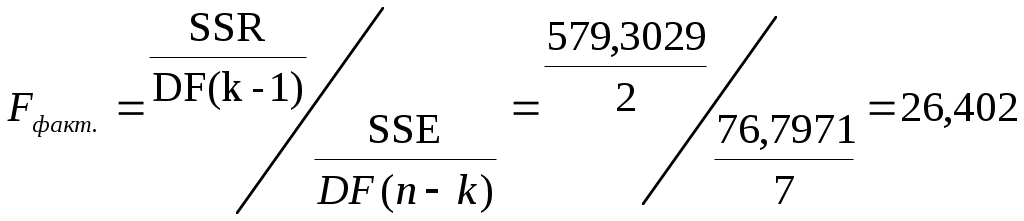 дает F-критерий Фишера : Вероятность случайного значения F - критерия = 24,402 составляет 0,0000000000005, что значительно меньше 0,05. Следовательно, полученное значение неслучайно, оно сформировалось под влиянием существенных факторов. То есть подтверждается статистическая значимость всего уравнения, его параметров и показателя тесноты связи – коэффициента множественной корреляции. (Fкрит. = 4,74, т.е. Fфакт.>Fкрит.). Общий вывод по построенной регрессионной модели состоит в том, что на увеличение объёма продаж нового моющего средства значимо повлияла реклама на радио и телевидении: при увеличении расходов на рекламу – возрастал объем продаж. Затраты же на демонстрацию моющего средства в магазинах не оказали существенного влияния на рост объёма продаж. Прогноз по модели множественной регрессии осуществляется по тому же принципу, что и для парной регрессии. Для получения прогнозных значений мы подставляем значения хi в уравнение для получения значения  . Предположим, что мы хотим узнать ожидаемый объем продаж моющего средства, при условии, что затраты на теле и радио рекламу составят 10 условных денежных единиц, а на демонстрацию в магазинах – 5 условных денежных единиц: (у.е.)Качество прогноза – неплохое, поскольку в исходных данных таким значениям независимых переменных соответствует значение равное 70 у.е.Мы так же можем вычислить интервал прогноза как  - доверительный интервал для ожидаемого значения при заданных значениях независимых переменных: ,где MSE – остаточная дисперсия, а  - стандартная ошибка оценки уравнения. Задачи 3, 4 и 5 посвящены теме «Временные ряды в эконометрических исследованиях», и, прежде всего проблеме автокорреляции уровней временного ряда и ее последствиям, а также наличию во временном ряде тенденции. Задача 3. Рассмотрим методику решения задачи на практическом примере: Имеются следующие данные о расходах семьи на товар "А" в 1994-1999 гг.:
Приступая к выполнению пункта 1, изучите вопрос об измерении автокорреляции уровней временного ряда. Коэффициент автокорреляции первого порядка есть линейный коэффициент корреляции между уровнями исходного временного ряда и уровнями того же ряда сдвинутыми на один момент времени. Его расчет производится по стандартным формулам для расчета линейного коэффициента корреляции: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
)
