Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н

• Название: Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
• Анкор: Пример работы по эконометрике
• Дата: 27.02.2022
• Размер: 1.23 Mb.
• Имя файла: пример работы по эконометрике.doc
• Тип: Методические указания; #374893
• страница: 4 из 10

,

где y_{t + 1} - уровни, сдвинутые по отношению к уровням исходного ряда на 1 год.

Заметим, что расчет должен быть осуществлен для пар наблюдений ( , , причем общее число пар наблюдений, по которым производится расчет, равно (n - 1). Близкое по абсолютной величине к единице значение коэффициента автокорреляции первого порядка свидетельствует о высокой тесноте связи между текущими и непосредственно предшествующими уровнями временного ряда или, иными словами, о наличии во временном ряде тенденции.
В соответствии с условиями нашей задачи проведем расчеты

Годы	yt	yt+1	yt*yt+1	yt2	yt+12
1994	30	35	1050	900	1225
1995	35	39	1365	1225	1521
1996	39	44	1716	1521	1936
1997	44	50	2200	1936	2500
1998	50	53	2650	2500	2809
Итого	198	221	8981	8082	9991

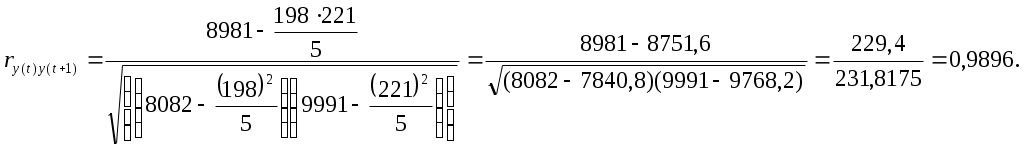
Коэффициент автокорреляции первого порядка равен 0,9896, что свидетельствует о тесной прямой связи между текущими и непосредственно последующими уровнями временного ряда.
В пункте 2 требуется определить функциональную форму и найти параметры уравнения, наилучшим образом описывающего тенденцию (тренд). Для определения вида тренда рассчитайте следующие показатели динамики:

а) цепные абсолютные приросты: ;

б) абсолютные ускорения уровней ряда, или вторые разности: ;

в) цепные коэффициенты роста: .

Проанализируйте полученные результаты.

Если приблизительно одинаковы цепные абсолютные приросты, то для описания тенденции временного ряда следует выбрать линейный тренд: .

Если примерно постоянны абсолютные ускорения уровней ряда, следует выбрать параболу второго порядка: .

Если примерно одинаковы цепные коэффициенты роста, моделирование тенденции следует проводить с использованием экспоненциальной кривой: .

Для расчета параметров уравнения тренда примените обычный МНК. В случае нелинейных зависимостей проведите линеаризацию исходной функции.

Дайте интерпретацию параметров тренда.

Коэффициент регрессии b в линейном тренде есть средний за период цепной абсолютный прирост уровней ряда.

В экспоненциальной функции величина представляет собой средний за период цепной темп роста уровней ряда.

Начальный уровень ряда в момент (период времени) t = 0 в линейном тренде выражается параметром а, в экспоненциальном тренде - величиной .
Для нашей задачи проведем следующие расчеты:

Годы	yt
1994	30	-
1995	35	5		1,1667
1996	39	4	-1	1,1143
1997	44	5	1	1,1282
1998	50	6	1	1,1364
1999	53	3	-3	1,0600

Очевидно, в данном случае для описания тренда можно выбрать линейную модель: .

Для расчета параметров уравнения тренда применим МНК.
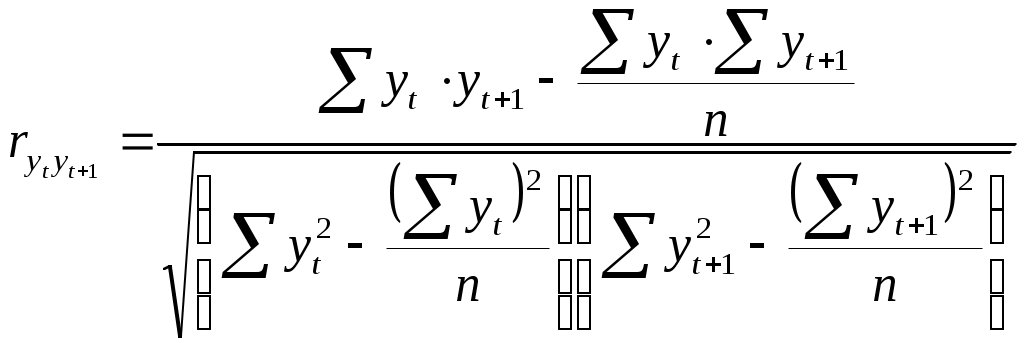