Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Величина этого коэффициента корреляции еще более убедительно свидетельствует о сопутствии рядов во времени. Пункт 4. По аналогии с коэффициентами корреляции параметры уравнения регрессии по временным рядам определяют также не по исходным их уровням, а по последовательным разностям, либо отклонениям от тренда. Обратите внимание на интерпретацию параметров, полученных уравнений регрессии: - если уравнение регрессии построено по первым разностям, то коэффициент регрессии b характеризует изменение прироста результативного признака при изменении прироста факторного признака на единицу. Сделайте общий вывод о наличии и тесноте причинно-следственной связи между изучаемыми временными рядами, укажите ее направление. Определим параметры уравнения парной линейной регрессии по первым разностям. Расчет осуществляется обычным методом наименьших квадратов:
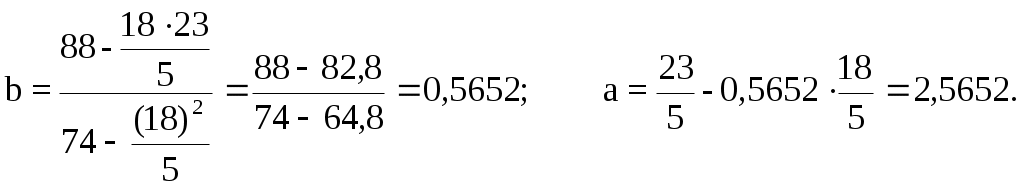 Отсюда, модель имеет вид: Коэффициент регрессии b = 0,5652 означает, что с изменением прироста душевого дохода на 1 процентный пункт расходы на товар "А" изменяются с ускорением, равным 0,5652 руб. Задача 5 посвящена методике выявления сезонной компоненты в рядах динамики, построению моделей с аддитивной и мультипликативной сезонными компонентами и прогнозированию по этим моделям. Для выявления тренда и наличия сезонной компоненты постройте график ряда динамики (пункт 1). При построении графика ряда динамики по оси абсцисс откладываются временные промежутки, а по оси ординат – уровни ряда. Приступая к выполнению пункта 2, изучите вопрос об особенностях анализа сезонных колебаний. Сезонная колеблемость в рядах динамики может иметь аддитивный и мультипликативный характер. Если сезонная вариация постоянна в различных временных периодах, то для анализа временного ряда подходит модель с аддитивной компонентой. Если сезонная вариация не является константой, например, увеличивается с возрастанием значений тренда, то для анализа лучше подходит модель с мультипликативной компонентой, в которой значения сезонной компоненты представляют собой определенную долю трендового значения. В зависимости от особенностей сезонной вариации сделайте выбор между моделями с аддитивной и мультипликативной компонентами. Каждой из этих моделей соответствуют различные методы расчета сезонной компоненты тренда, использующие сочетание методов скользящего среднего и линейной регрессии. Следует помнить, что поскольку сезонные колебания характеризуются относительно небольшими временными интервалами, то прогнозирование по моделям с сезонной компонентой – также краткосрочное. Модель с аддитивной компонентой. Если сезонная компонента переменной А – постоянна, модель фактических значений переменной А можно представить следующим образом: Фактическое значение = = Трендовое значение + Сезонная вариация + Ошибка, то есть: A = T + S + E. Модель с мультипликативной компонентой. Если значение сезонной компоненты переменной А, не является константой, а представляет собой определенную долю трендового значения, т.е. значения сезонной компоненты увеличиваются с возрастанием значений тренда, модель фактических значений переменной А можно представить следующим образом: Фактическое значение = = Трендовое значение т.е. А = T В моделях, как с аддитивной, так и с мультипликативной компонентой общая процедура анализа примерно одинакова: Шаг 1. Расчет значений сезонной компоненты. Шаг 2. Десезонализация данных. Для модели с аддитивной компонентой он состоит в вычитании сезонной компоненты из фактических значений. Для модели с мультипликативной компонентой – в расчете отношений между фактическими значениями и сезонной составляющей. Расчет тренда на основе полученных десезонализированных данных. Шаг 3. Расчет ошибок как разности между фактическими и трендовыми значениями. В мультипликативной модели можно рассчитать ошибки еще и как отношение между фактическими и трендовыми значениями. Шаг 4. Расчет среднего линейного отклонения или среднеквадратической ошибки для обоснования соответствия модели исходным данным или для выбора из множества моделей наилучшей. Для того чтобы элиминировать влияние сезонной компоненты (пункт 3) воспользуйтесь методом скользящей средней. Если сезон состоит из 4-х кварталов (год), следует провести сглаживание по 4-м точкам, если сезон состоит из 7-и дней (неделя) следует провести сглаживание по 7-и точкам и т.д. Значения уровней ряда, сглаженные по четному числу точек необходимо центрировать. Множество скользящих средних представляет наилучшую оценку искомого тренда. Процедуры сглаживания и центрирования одинаковы при построении моделей с аддитивной и мультипликативной компонентами. Полученные значения тренда используйте для нахождения оценок сезонной компоненты. Для модели с аддитивной компонентой: A – T = S + E. Для модели с мультипликативной компонентой: А/Т= S Найдите средние значения сезонных оценок для каждого года (недели и т.п.). Эта процедура позволяет уменьшить некоторые значения ошибок. Скорректируйте средние значения. Для модели с аддитивной компонентой корректировка состоит в увеличении или уменьшении средних значений на одно и то же число таким образом, чтобы их общая сумма была равна нулю. Это необходимо для того, чтобы усреднить значения сезонной компоненты в целом за период. Обычно корректирующий фактор рассчитывается путем деления суммы оценок сезонных компонент на число сезонов. В мультипликативной модели значения сезонной компоненты - это относительные величины. Поэтому необходимо, чтобы их сумма была равна числу сезонов, а не нулю, как в случае с аддитивной моделью. Если это не так, произведите корректировку значений сезонной компоненты. Шаг 2 состоит в десезонализации исходных данных (пункт 4). В модели с аддитивной компонентой она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал (день и т.п.), то есть: A – S = T + E. В модели с мультипликативной компонентой процедура десезонализации осуществляется по формуле: А/S= T Новые оценки тренда, которые все еще содержат ошибку, используйте для построения модели основного тренда. Нанесите эти значения на исходную диаграмму, сделайте вывод о наличии тренда. Пункт 5 посвящен подбору уравнения тренда с аддитивной или мультипликативной компонентой. При этом выбор функциональной формы тренда осуществляется, исходя из общих принципов, изложенных в пункте 2 к задаче 3. Предположим, например, что тренд – линейный. Уравнение линейного тренда имеет вид: где х – порядковый номер квартала, а и b – параметры уравнения парной регрессии. Поскольку предполагается, что тренд имеет линейный характер, то значения параметров линии, аппроксимирующей тренд, найдите методом наименьших квадратов: где y = T + E, 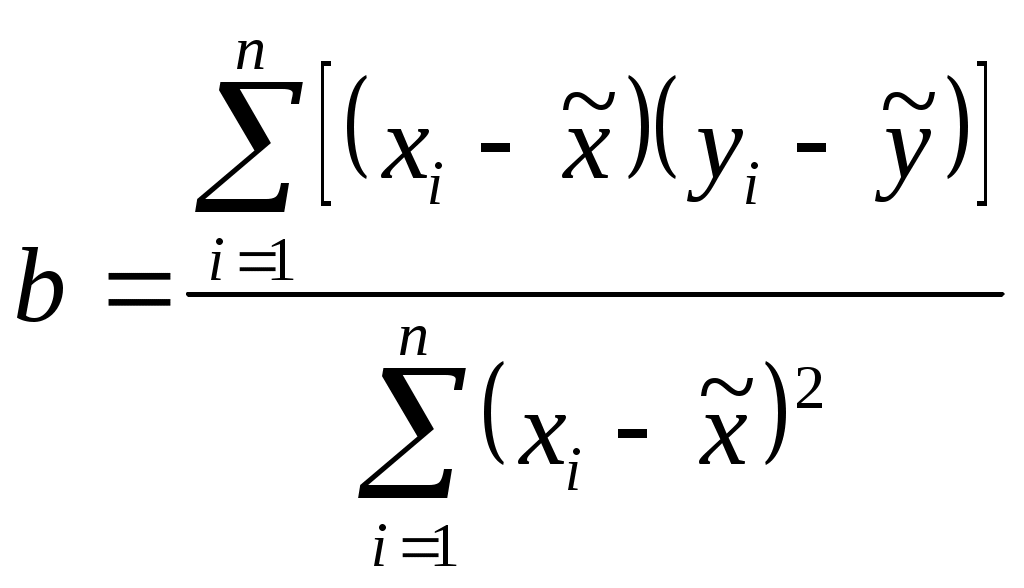 , ,Пункт 6 заключается в расчете ошибки (Е), среднего абсолютного отклонения (MAD) и среднеквадратической ошибки (MSE) модели. Расчет этих показателей соответствует шагу 3 алгоритма и предшествует составлению прогноза. Осуществите расчет ошибок или остатка. В аддитивной модели он осуществляется по формуле: Е = А - S - Т. В мультипликативной: Е = А/(Т или Е = А - (Т Найдите меру соответствия модели исходным данным, т.е. определите ту часть колеблемости уровней ряда, которую невозможно объяснить с помощью построенной модели. Для этого используйте среднее абсолютное отклонение (mean absolute deviation - MAD) и среднеквадратическую ошибку (mean square error - MCE): Целесообразно использовать обе меры, так как последняя из них резко возрастает при наличии высоких ошибок. Пункт 7 состоит в прогнозировании на основании полученных моделей. Прогнозные значения по модели с аддитивной компонентой рассчитайте по формуле: F = T + S. В модели с мультипликативной компонентой используйте следующий алгоритм: F= Т Не следует забывать: чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза. Рассмотрим практическую реализацию методики решения задачи для модели с аддитивной компонентой. В таблице 1 представлено количество продукции, проданной компанией FORA LTD в течение последних 13 кварталов. Таблица 1. Количество продукции, проданной в течение последних 13 кварталов
Построим график, позволяющий сделать выводы о типе модели: 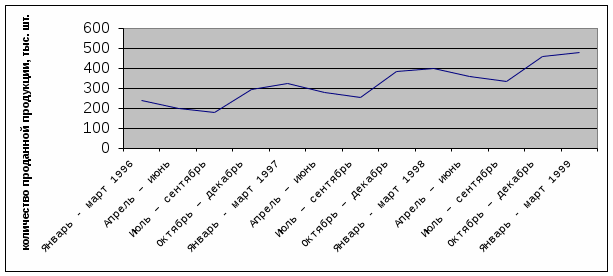 Стабильность сезонной компоненты указывает на то, что модель с аддитивной компонентой подходит для анализа этого временного ряда. То есть фактические объемы продаж можно выразить следующим образом: A = T + S + E Для того чтобы элиминировать влияние сезонной компоненты воспользуемся методом скользящей средней, которую рассчитаем с интервалом в три месяца. Этот расчет и все последующие проведем в таблице 2. Таблица 2 . Расчет по 4 точкам центрированных скользящих средних значений тренда для модели A – T = S + E
Просуммировав первые 4 значения, получим общий объем продаж в 1996 году. Разделив эту сумму на 4, найдем средний объем продаж в каждом квартале 1996 года: (239 + 201 + 182 + 297)/4 = 299,75. Полученное значение уже не содержит сезонной компоненты, так как представляет собой среднюю величину за год. У нас появилась оценка значения тренда для середины года, то есть для точки, лежащей в середине между кварталами II и III. Последовательно продвигаясь вперед с шагом в один квартал, рассчитаем средние квартальные значения для промежутков: апрель 1996 – март 1997 (251), июль 1996 – июнь 1997 (270,25) и т.д. Данная процедура позволяет генерировать скользящие средние по 4 точкам исходного множества данных. Получаемое таким образом множество скользящих средних представляет собой наилучшую оценку искомого тренда. Теперь полученные значения тренда можно использовать для нахождения оценок сезонной компоненты. Мы рассчитываем: |
