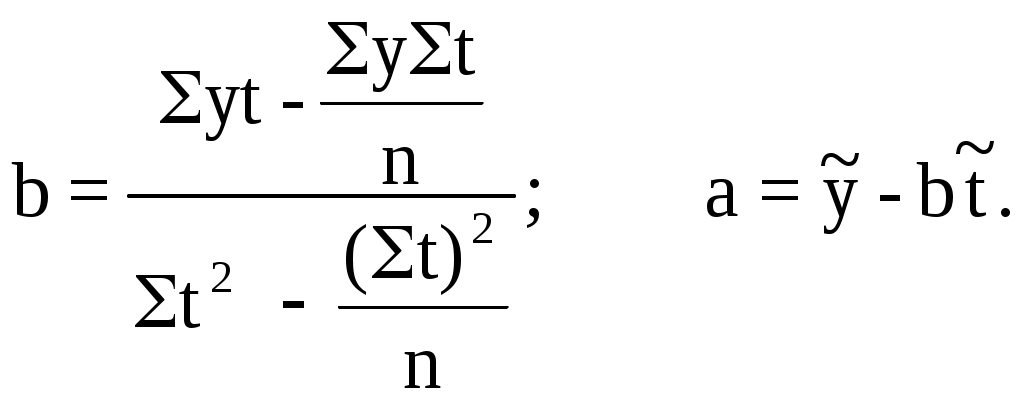Пример работы по эконометрике. пример работы по эконометрике. Методические указания по выполнению контрольной работы РостовнаДону Авторы Ниворожкина Л. И., Житников И. В., Федосова О. Н
 Скачать 1.23 Mb.
|
|
|
| | t | yt | t2 | yt*t |
| 1994 | -2,5 | 30 | 6,25 | -75 |
| 1995 | -1,5 | 35 | 2,25 | -52,5 |
| 1996 | -0,5 | 39 | 0,25 | -19,5 |
| 1997 | 0,5 | 44 | 0,25 | 22 |
| 1998 | 1,5 | 50 | 2,25 | 75 |
| 1999 | 2,5 | 53 | 6,25 | 132,5 |
| Итого | 0,00 | 251 | 17,5 | 82,5 |
Таким образом, трендовое линейное уравнение регрессии имеет вид:
.Дадим интерпретацию параметров тренда.
Коэффициент регрессии (b) в линейном тренде показывает средний за период цепной абсолютный прирост уровней ряда. В нашем примере b = 4,7143, следовательно расходы на товар "А" в среднем за год увеличиваются на 4,7143 у.е. Свободный член (а) в линейном тренде выражает начальный уровень ряда в момент (период времени) t = 0. В нашей нумерации t = 0 приходится на период времени между 1996 и 1997 гг., что несколько затрудняет его интерпретацию. В нашем случае а = 41,8333 у.е. – это расходы семьи на товар "А" за вторую половину 1996 и первую половину 1997 гг.
В случае нелинейных зависимостей необходимо провести линеаризацию исходной функции.
Пункт 3. Точечный прогноз по уравнению тренда - это расчетное значение переменной
, полученное путем подстановки в уравнение тренда соответствующих значений t. Интервальный прогноз рассчитывается в соответствии с методикой, изложенной для уравнения парной линейной регрессии (см. указания к пункту 5 задачи 1).Найдем прогноз расходов на товар "А" на 2000 год.
В нашей нумерации 2000 год соответствует моменту времени t = 3,5. Отсюда,
Следовательно, точечная оценка расходов семьи на товар "А" на 2000 год составляет 58,3333 у.е.
Определим границы доверительного интервала, в котором с заданной надежностью γ будут находиться расходы семьи на товар "А" в 2000 году. Общепринятый в экономике уровень надежности γ = 1 - α = 1 - 0,05 = 0,95 или 95%
,где
- прогноз значения переменной y на момент (период) времени t; 
- точечная оценка значения переменной y на момент (период) времени t;
- предельная ошибка прогноза.Для того, чтобы получить интервальную оценку, определим величину предельной ошибки прогноза.
Она рассчитывается по формуле:
,где
- табличное значение t - критерия Стьюдента для уровня значимости α и числа степеней свободы (k = n - 2); 
- стандартная ошибка точечного прогноза, которая, в свою очередь, рассчитывается по формуле:
,где
- длина периода упреждения (срок прогноза).Расчеты проведем в рабочей таблице.
| | t | | |  |  |
| 1994 | -2,5 | 30 | 30,0476 | -0,0476 | 0,0023 |
| 1995 | -1,5 | 35 | 34,7619 | 0,2381 | 0,0567 |
| 1996 | -0,5 | 39 | 39,4762 | -0,4762 | 0,2268 |
| 1997 | 0,5 | 44 | 44,1905 | -0,1905 | 0,0363 |
| 1998 | 1,5 | 50 | 48,9048 | 1,0952 | 1,1995 |
| 1999 | 2,5 | 53 | 53,6190 | -0,6190 | 0,3832 |
| Итого | 0,00 | 251 | 197,3810 | 0,0000 | 1,9048 |
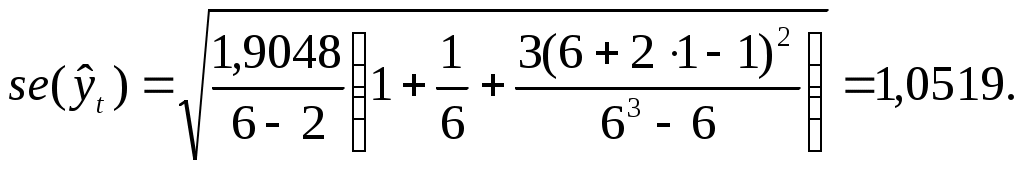
Табличное значение t - критерия Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = 6 – 2 = 4 составляет 2,78, т.е.
=2,78.Отсюда,
Таким образом,
P
=0,95
.С вероятностью 0,95 можно ожидать, что в 2000 году расходы семьи на товар "А" будут находиться в пределах от 55,4089 до 61,2577 у.е.
Обратите внимание на то, что приведенные формулы верны только для уравнения парной регрессии, линейной по параметрам.
Задача 4.
Рассмотрим методику решения задачи на примере:
Имеются следующие данные о величине дохода в расчете на одного члена семьи в процентах к 1994 году и о расходах семьи на товар "А" в 1994-1999 гг.:
| Годы | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Расходы на товар "А", руб. | 30 | 35 | 39 | 44 | 50 | 53 |
| Доход на одного члена семьи в процентах к 1994 году, % | 100 | 103 | 105 | 109 | 115 | 118 |
Пункт 1. Определение функциональной формы трендового уравнения регрессии описано в пункте 2 к задаче 3.
Пункты 2-3. При измерении корреляции между двумя временными рядами следует учитывать возможность наличия ложной корреляции, обусловленной простым сопутствием временных рядов. Для того чтобы устранить ложную корреляцию, следует определять степень тесноты связи не самих уровней временных рядов, а их последовательных (первых или вторых) разностей или отклонений от трендов (если последние не содержат тенденции).
Сделайте вывод о наличии или отсутствии ложной корреляции при разных способах измерения связи между исследуемыми временными рядами, поясните причины существования ложной корреляции.
По данным примера рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по исходным уровням ряда: