лабы информатика. Методические указания по выполнению лабораторных работ для студентов фэуб специальностей 080200 Менеджмент
 Скачать 10 Mb.
|
|
Вариант 22. Брокеру биржи клиент поручил разместить 100 000 долл. США на фондовом рынке, сформировать портфель с ценными бумагами, чтобы получить максимальные годовые проценты с вложенного капитала. Выбор ограничен четырьмя возможными объектами инвестиций-акций А, В, С, Д, которые позволяют получить доход в размерах соответственно 6, 8, 10 и 9% годовых от вложенной суммы. При этом клиент поручил не менее половины инвестиций вложить в акции А и В. С целью обеспечения ликвидности не менее 25% общей суммы капитала нужно поместить в акции Д. Учитывая прогноз на изменение ситуации в будущем, в акции С можно вложить не более 20% капитала. Специфика налогообложения указывает на необходимость вложения в акции А не менее 30% капитала. Определите распределение инвестиций капитала, обеспечивающего максимальный годовой процентный доход. Лабораторная работа №5 Задачи управления с двухиндексными переменными Цель работы: научиться решать задачи целочисленного линейного программирования и задачи с двухиндексными переменными. Содержание работы:
1 Задача целочисленного программирования Значительная часть экономических задач, относящихся к задачам линейного программирования, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например, распределение производственных заданий между предприятиями, раскрой материалов, загрузка оборудования, распределение судов по линиям, самолетов по рейсам и т.д. Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включает дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами. Пример 1. Фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входят 3 фунта азотных, 4 фунта фосфорных и один фунт калийных удобрений, а в улучшенный — 2 фунта азотных, 6 фунтов фосфорных и 2 фунта калийных удобрений. Известно, что для некоторого газона требуется, по меньшей мере, 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3 долл., а улучшенный — 4 долл. Сколько и каких наборов удобрений надо купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость? Решение. Пусть х — количество обычных наборов удобрений, у — количество улучшенных наборов удобрений. L(x, у) = 3х + 4у →min при ограничениях: 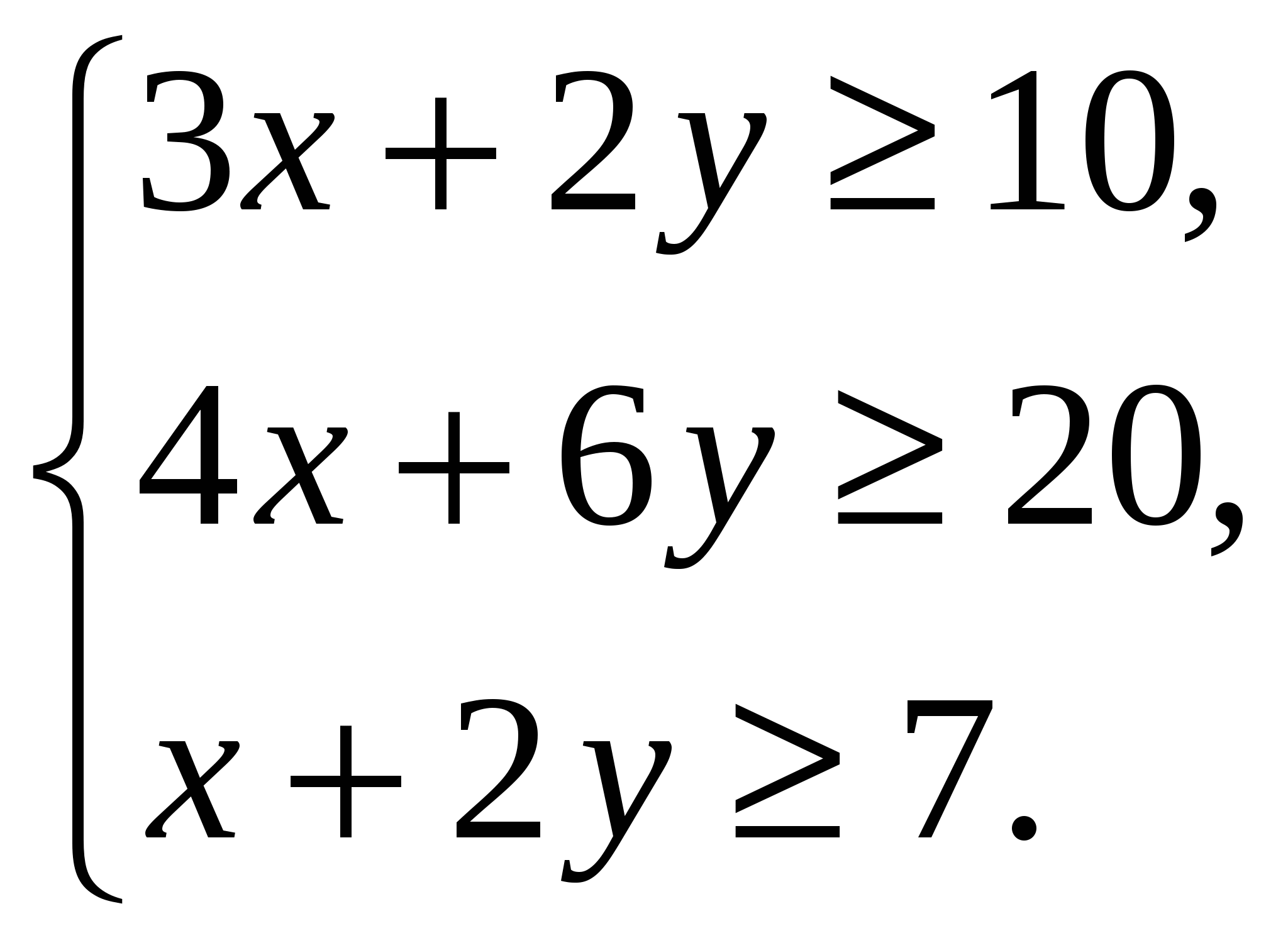 Воспользуемся возможностями Excel и введем уравнения для ограничений и ЦФ с помощью мастера функций. Здесь выберем из категории Математические функцию СУММПРОИЗВ. Примечание. Функция СУММПРОИЗВ(массив1; массив2; массив3; …) – перемножает соответствующие элементы заданных массивов и возвращает сумму произведений. Массив1; массив2; массив3;…- это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить. Аргументы, которые являются массивами, должны иметь одинаковые размерности. Если это не так, то функция СУММПРОИЗВ возвращает значение ошибки #ЗНАЧ!. СУММПРОИЗВ трактует нечисловые элементы массивов как нулевые. Используя обозначения соответствующих ячеек формулу для расчета ограничений можно записать как сумму произведений каждой из ячеек, отведенных для значений коэффициентов (B3, В4), на соответствующую ячейку, отведенную для переменных задачи (F3, F4) и вычесть, то есть 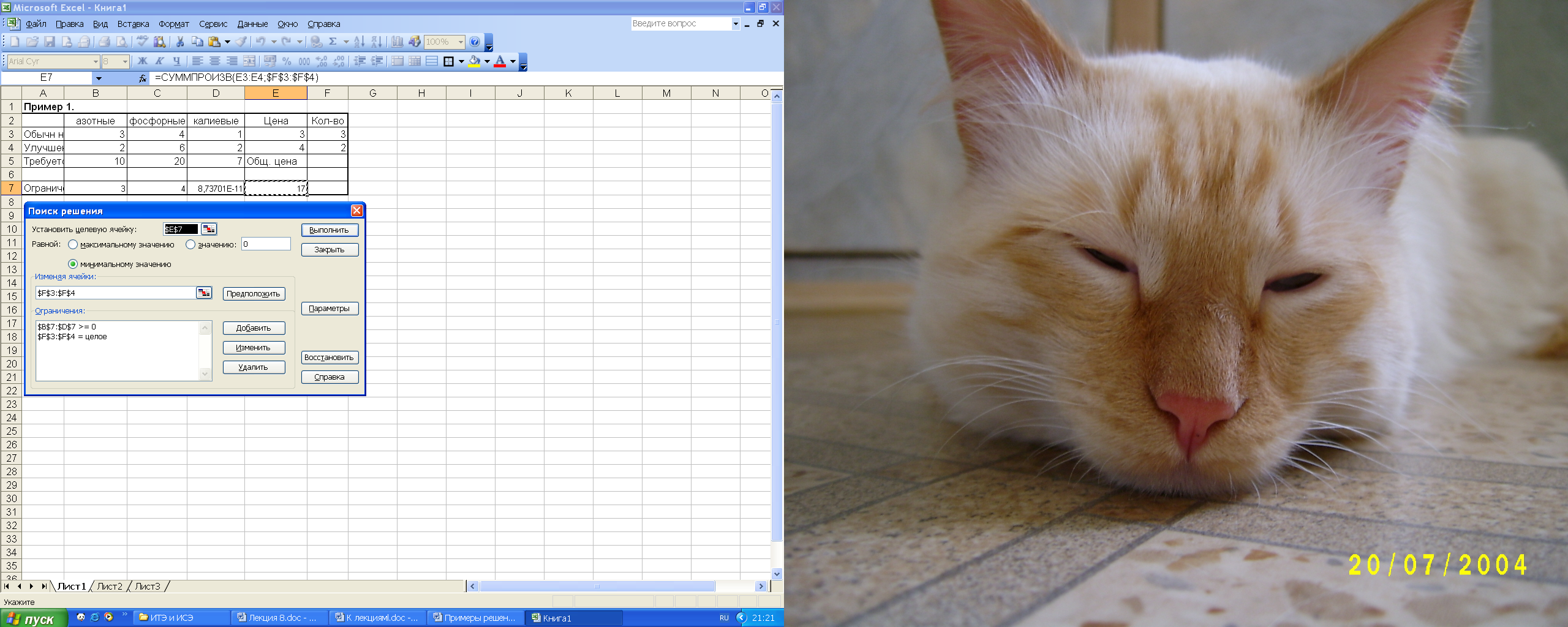 . То есть чтобы задать эту формулу необходимо в ячейку В7 ввести следующее выражение и нажать клавишу «Enter»=СУММПРОИЗВ( В3:В4, $F$3:$F$4) – В5. Она скопирована в C7:Е7(в ячейке Е7 она скорректирована, убрано вычитаемое Е5). Выделим ячейку с целевой функцией и вызовем «Сервис/ Поиск решения». В диалоговом окне укажем: «Установить целевую ячейку:» $Е$7, «минимальное значение», «изменяя ячейки» $F$3:$F$4, «ограничения» $B$7:$D$7>=0. В окне «Параметры» установим флажок «Линейная модель» и «Неотрицательные значения». Запустим выполнение. Поиск решения вернет результат: х= 1.5,у = 2.15. Целевая функция равна 15.5. Но наборы удобрений нельзя покупать частями! Нужно наложить еще одно ограничение: х, у — целые числа. Вновь вызываем Решатель, нажимаем кнопку «Добавить» и в диалоговом окне «Добавление ограничения» указываем, что $F$3:$F$4 — целые (в том же выпадающем списке, откуда ранее мы выбирали символ для ограничения). Нажимаем «ОК». Запустим выполнение. На этот раз получим значение целевой функции 17 (естественно, оно ухудшилось), а количество наборов стало таким: х = 3, у = 2.  Пример 2. В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес одного изделия составляют 400 руб. и 12 кг для первого типа, 500 руб. и 16 кг для второго типа, 600 руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить максимальную и минимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий. Решение. x, y, z – количество комплектующих 1-го, 2-го и 3-го типа. L(x, у, z) = 400х + 500у+600z→min(max) Ограничения  . Целевая функция равна 12600 руб. и 10500 руб.К задачам целочисленного программирования относят также задачи, где некоторые переменные могут принимать всего два значения: 0 и 1. Такие переменные называют булевыми, двоичными, бинарными. Пример 3. Имеются 6 предметов, каждый из которых характеризуется весом и ценой (см. рис.). Нужно выбрать из них такие предметы, чтобы их общий вес не превышал 12, а суммарная цена была максимальной (так называемая "задача о рюкзаке"). Решение. В блоке А20:А25 размещены условные названия предметов, а в соседних столбцах — их вес и цена. В блоке D20:D25 фиксируется наличие (1) или отсутствие (0) предмета в наборе. Блокам даны имена в соответствии с их заголовками. В Решателе задаем: максимизировать $А$27 по переменным "наличие" при ограничениях $А$26<=0 и наличие=двоичное. Последнее ограничение задается так. В диалоговом окне "Добавление ограничения" сначала нажимаем F3 и вставляем имя "наличие", в выпадающем списке выбираем "двоич". После запуска Решателя он выдает сообщение – значение целевой ячейки равно 23, а двоичные значения: 0, 1,0, 0, 1, 0, т.е. нужно выбрать второй и пятый предметы. 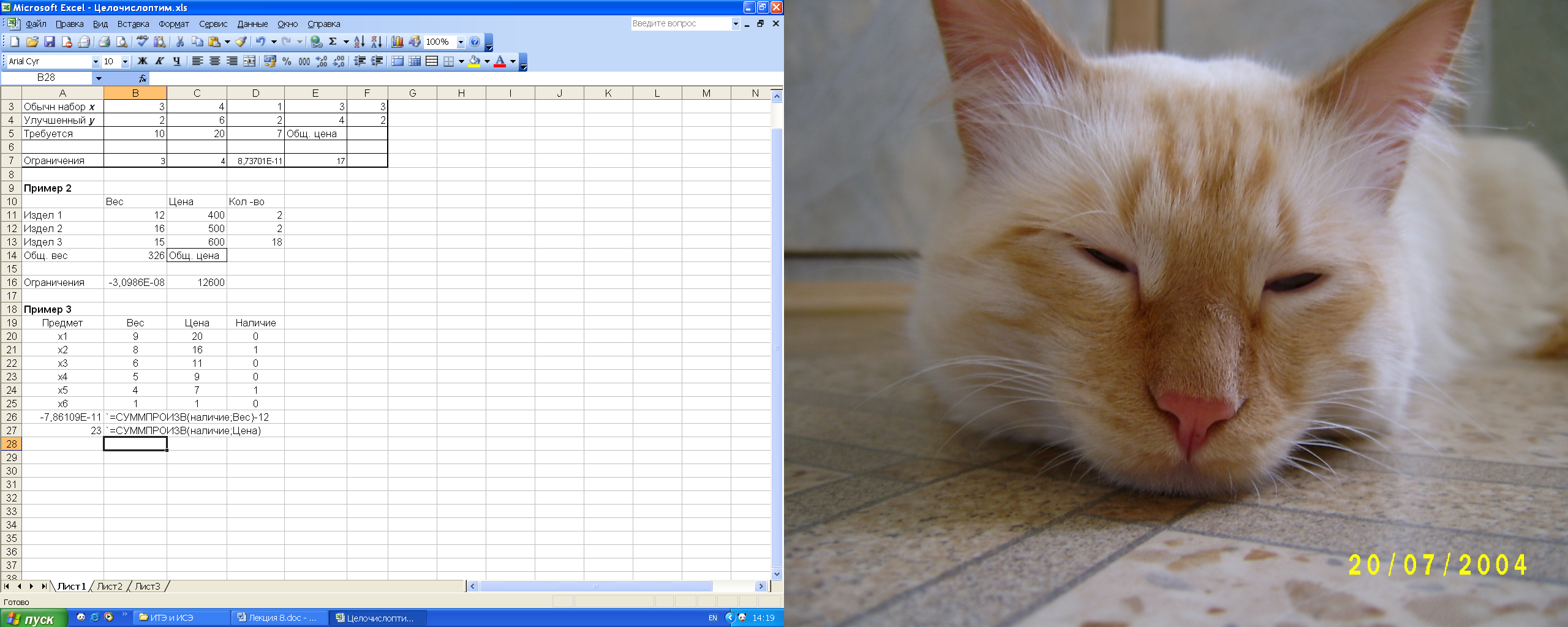 2 Двухиндексные задачи ЛП Выполнить заказ по производству 32 изделий  и 4 изделий  взялись бригады  и  . Производительность бригады по производству изделий и составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады – соответственно 1 и 3 изделия в час, а ее фонд рабочего времени – 4 ч. Затраты, связанные с производством единицы изделия, для бригады равны соответственно 9 и 20 руб., для бригады – 15 и 30 руб.Составьте математическую модель задачи, позволяющую найти оптимальный объем выпуска изделий, обеспечивающий минимальные затраты на выполнение заказа. Решение. Искомыми величинами в задаче являются объемы выпуска изделий. Изделия будут выпускаться двумя бригадами и . Поэтому необходимо различать количество изделий , произведенных бригадой , и количество изделий И1, произведенных бригадой . Аналогично, объемы выпуска изделий бригадой и бригадой также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи  – количество изделий  (j=1,2), изготавливаемых бригадой  (i=1,2), а именно,
Целевая функция Целью решения задачи является выполнение плана с минимальными затратами, т.е. критерием эффективности решения служит показатель затрат на выполнение всего заказа. Поэтому ЦФ должна быть представлена формулой расчета этих затрат. Затраты каждой бригады на производство одного изделия и известны из условия. Таким образом, ЦФ имеет вид  ,  Ограничения Возможные объемы производства изделий бригадами ограничиваются следующими условиями:
Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:
Для удобства составления ограничений запишем исходные данные в виде таблицы 1. Таблица 1
Ограничения по заказу изделий имеют следующий вид  и .Ограничение по фондам времени содержательную форму  и  .Проблема заключается в том, что в условии задачи прямо не задано время, которое тратят бригады на выпуск одного изделия или , т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е. .Поэтому используя таблицу 1, получаем следующую информацию:
Запишем ограничения по фондам времени в математическом виде  и  .Задачи для самостоятельного решения ЗАДАЧА 1. Авиакомпания МОГОЛ по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно. Эксплуатация 1 самолета первого типа обойдется 5000$, а второго 9000$. Сколько надо использовать самолетов каждого типа c минимальной стоимостью эксплуатации, если для формирования экипажей имеется не более 60 человек. Ответ: 6 самолетов I-го типа и 8 самолетов II-го. Мин. стоимость эксплуатации 10200$. | |||||||||||||||||||
– количество изделий 
– количество изделий 
– количество изделий 
– количество изделий 
ч тратит бригада 
ч тратит бригада 
;
ч тратит бригада 
на производство одного изделия 
ч тратит бригада