лабы информатика. Методические указания по выполнению лабораторных работ для студентов фэуб специальностей 080200 Менеджмент

• Название: Методические указания по выполнению лабораторных работ для студентов фэуб специальностей 080200 Менеджмент
• Анкор: лабы информатика.doc
• Дата: 11.02.2017
• Размер: 10 Mb.
• Имя файла: лабы информатика.doc
• Тип: Методические указания; #2540
• страница: 10 из 15

[тыс.руб./сутки],

.

Ограничения. Возможные объемы производства красок и ограничиваются следующими условиями:

• 
  количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
  

.

Аналогична математическая запись ограничения по расходу В

.

согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;

.

• 
  объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта; .
  
• 
  объемы производства красок не могут быть отрицательными.
  

Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:

1. 
   расходом ингредиентов;
   
2. 
   рыночным спросом на краску;
   
3. 
   неотрицательностью объемов производства.
   

Третья группа ограничений - неотрицательность переменных x_i в математике называется граничными условиями.

Таким образом, математическая модель этой задачи имеет вид





Решение задачи

Решим поставленную задачу с помощью команд программы Excel Сервис, Поиск решения. Если в меню Сервис отсутствует команда Поиск решения, то необходимо выполнить последовательно: Сервис, Надстройка, Поиск решения.

Решение задачи начинаем с подготовки данных. Введем необходимые данные и ограничения следующим образом (Рис. 1).

Выделите ячейку С5 и откройте меню Сервис / Поиск решения. В диалоговом окне в поле ввода Установить целевую ячейку уже содержится адрес ячейки с целевой



Рис. 1

Теперь введите ограничения. Щелкните Добавить. Появится диалоговое окно «Добавление ограничения». В поле ввода «Ссылка на ячейку» укажите $B$8. Правее расположен список с условными операторами, в котором вы должны выбрать условие <=. В поле ввода «Ограничение» щелкните ячейку $С$8. Далее щелкните кнопку «Добавить» и введите ограничение $B$9<=$С$9 и так по порядку введите все ограничения.

Можно сделать проще: В поле ввода «Ссылка на ячейку» укажите блок $B$8: $B$11, а в поле ввода «Ограничение» выделите блок $С$8: $С$11. Нажмите «ОК».

Вы вернулись в окно «Поиск решения». Щелкните кнопку «Параметры». Откроется окно «Параметры поиска решения». Установите два флажка: «Линейная модель» (ваши ограничения и функция являются линейными по переменным х и у) и «Неотрицательные значения» (для переменных х и у). Щелкните «ОК» и окажитесь в исходном окне.

Нажмите кнопку «Выполнить». Появляется окно «Результаты поиска решения». В нем вы читаете сообщение «Решение найдено. Все ограничения и условия оптимальности выполнены». На выбор предлагаются варианты: «Сохранить найденное решение» или «Восстановить исходные значения». Выберите первое.

После нажатия «ОК» вид таблицы меняется: в ячейках хи у появляются оптимальные значения. Оптимальный план производства и соответствующая прибыль появятся в исходной таблице. Из нее следует, что оптимальным является производство 3,333 т краски А и 1,333 т краски Б. Этот объем производства обеспечивает максимальную прибыль 12666,7.
Задание

Решить методом линейного программирования задачи согласно своего варианта – номера компьютера на системном блоке. результаты решения –записать в отчёт по работе.

Вариант 1. Для изготовления двух видов продукции Р₁, Р₂ используют три вида сырья S₁, S₂ и S₃. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 1.2. Необходимо составить такой план продукции, чтобы при ее реализации получить максимальную прибыль.

Таблица 1.2

Вид сырья	Запас сырья	Кол-во ед. сырья, идущих на изготовление ед. продукции.
		Р1	Р2
S1	20	2	5
S2	40	8	5
S3	30	5	6
Прибыль от ед. продукции (руб.)		50	40

Обозначим через x₁ и х₂ количество единиц продукции Р₁ и Р₂ соответственно. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений,



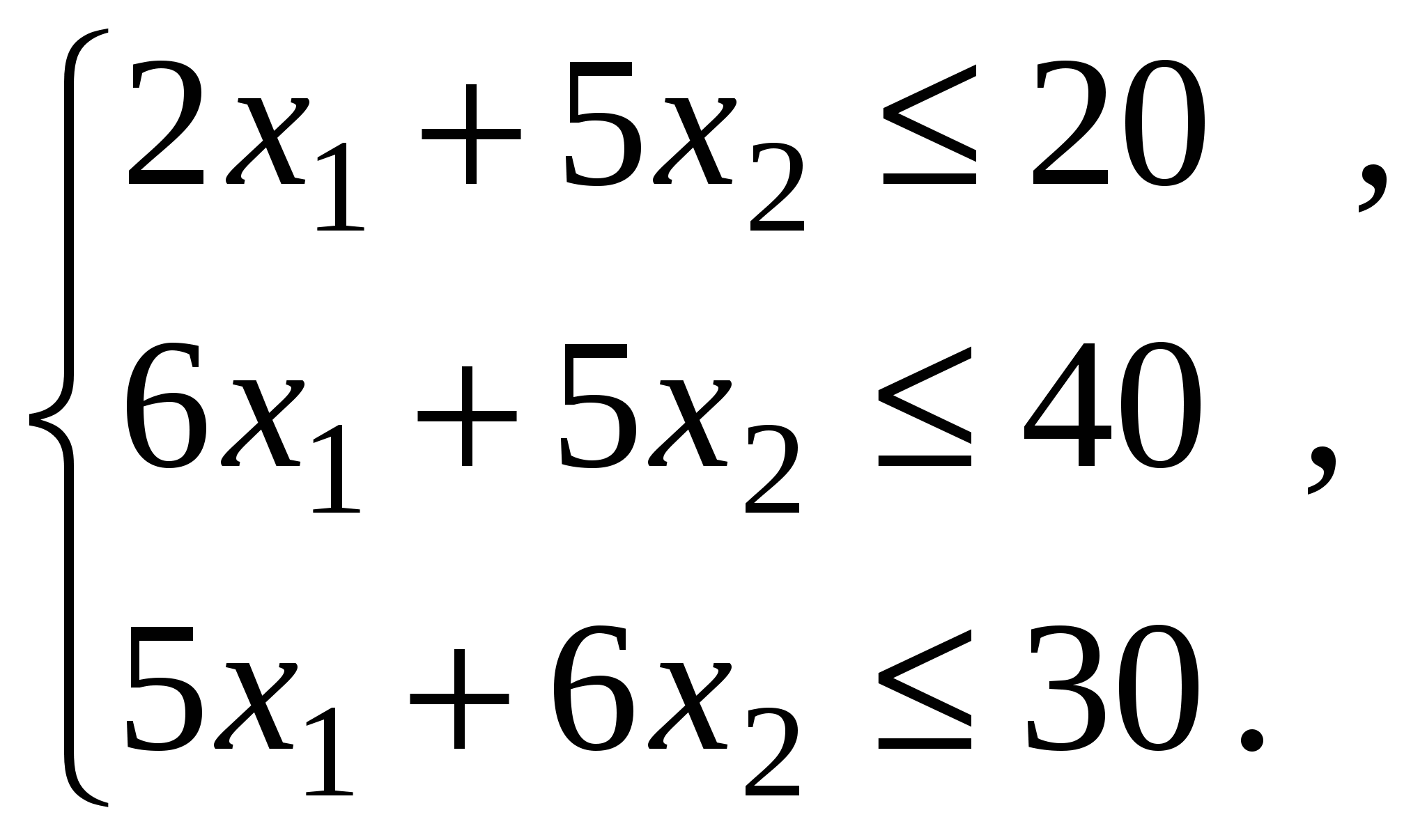
которая показывает, что количество сырья, расходуемое на ед. продукции, не может превысить имеющихся запасов. Конечная цель — получение максимальной прибыли, выразим как функцию двух переменных .
Вариант 2. Задача составления рациона

При откорме каждое животное ежедневно должно получить не менее 9 ед. питательного вещества S₁, не менее 8 ед. вещества S₂ и не менее 12 ед. вещества S₃ . Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в табл. 1.3

Таблица 1.3

Питательные вещества	Кол-во ед. питательных веществ в 1кг. корма
	Корм 1	Корм 2
S1	3	1
S2	1	2
S3	1	6
Стоимость 1 кг. корма (руб.)	4	6

Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.

Для составления математической модели обозначим через x₁ и х₂ соответственно количество корма I и II в дневном рационе. Принимая во внимание значения табл. 1.3, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество питательных веществ не меньше предусмотренного, получаем систему ограничений:



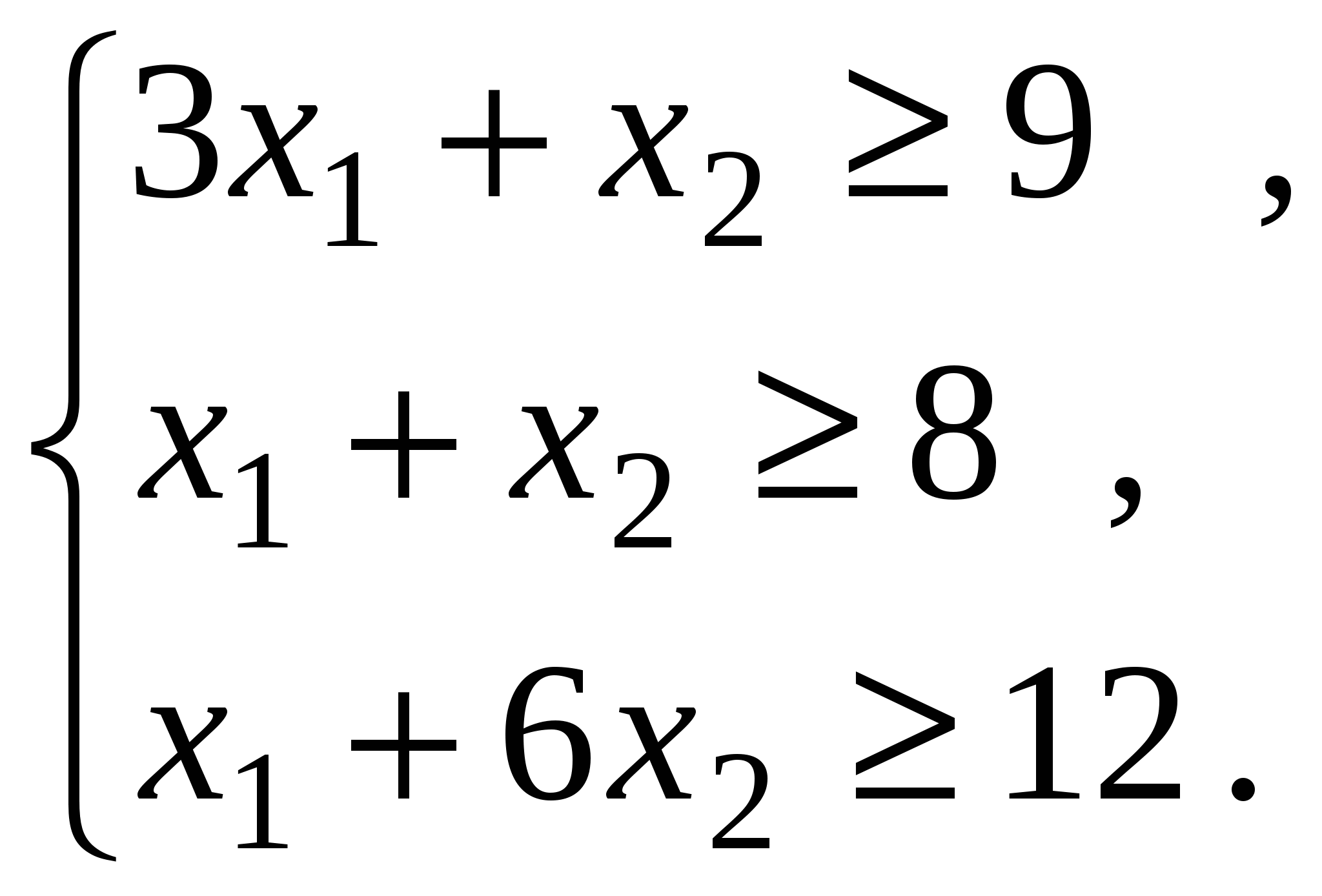
Не забываем об условии неотрицательности переменных (х₁ >=0 и х₂ >=0). Цель данной задачи — добиться минимальных затрат на дневной рацион, поэтому общую стоимость рациона можно выразить в виде линейной функции:

Вариант 3. Сформируйте вариант приготовления бензина АИ-80 и АИ-95, который обеспечивает максимальный доход от продажи, если имеется 5 т смеси 1-го сорта и 30 т смеси 2-го сорта. На изготовление бензина АИ-80 идет 60% смеси 1-го сорта и 40% смеси 2-го сорта, на изготовление бензина АИ-95 идет 80% смеси 1-го сорта и 20% смеси 2-го сорта. Реализуется 1 т бензина АИ-80 за 5000 руб., а 1 т АИ-95 - за 6000 руб.

Вариант 4. Фирма производит два безалкогольных широко популярных напитка «Колокольчик» и «Буратино». Для производства 1 л «Колокольчика» требуется 0,02ч работы оборудования, а для "Буратино" - 0.04ч, а расход специального ингредиента на них составляет 0,01 кг и 0,04 кг на 1 л соответственно. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24 ч работы оборудования. Доход от продажи 1 л " Колокольчика» составляет 0,25 руб., а "Буратино" - 0,35 руб.

Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи.

Вариант 5. Фирма производит для автомобилей запасные части типа А и В. Фонд рабочего времени составляет 5000 чел.-ч в неделю. Для производства одной детали типа А требуется 1 чел.-ч, а для производства одной детали типа В — 2 чел.-ч. Производственная мощность позволяет выпускать максимум 2500 деталей типа А и 2000 деталей типа В в неделю. Для производства детали типа А уходит 2 кг полимерного материала и 5 кг листового материала, а для производства одной детали типа В - 4 кг полимерного материала и 3 кг листового металла. Еженедельные запасы каждого материала - по 10 000 кг. Общее число производимых деталей в течение одной недели должно составлять не менее 1500 штук

Определите, сколько деталей каждого вида следует производить, чтобы обеспечить максимальный доход от продажи за неделю, если доход от продаж одной детали типа А и В составляет соответственно 1,1 руб. и 1,5 руб.

Вариант 6. Туристская фирма в летний сезон обслуживает в среднем 7500 туристов и располагает флотилией из двух типов судов, характеристики которых представлены в таблице.

Показатели	Судно
	I	II
Пассажировместимость, чел,	2000	1000
Горючее, т	12000	7000
Экипаж, чел.	250	100

В месяц выделяется 60 000 т горючего. Потребность в рабочей силе не превышает 700 человек.

Определите количество судов I и II типа, чтобы обеспечить максимальный доход, который составляет от эксплуатации судов I типа 20 млн. руб., а II типа - 10 млн. руб. в месяц.

Вариант 7. Фирма производит и продает столы и шкафы из древесины хвойных и лиственных пород. Расход каждого вида в кубометрах на каждое изделие задан в таблице.

Вид продукции	Расход древесины, м3		Цена изделия, тыс.руб.
	хвойные	лиственные
Стол	0,15	0,2	0,8
Шкаф	0,3	0,1	1,5
Запасы древесины, м3	80	40

Определите оптимальное количество столов и шкафов, которое следует поставлять на продажу для получения максимального дохода фирмы.

Вариант 8. С Курского вокзала Москвы ежедневно отправляются скорые и пассажирские поезда. Пассажировместительность и количество вагонов железнодорожного депо станции отправления указаны в таблице.

Тип вагона		Багажный	Почтовый	Жесткий	Купейный	Мягкий
Количество вагонов в поезде	скорый	1	1	8	4	1
	пассажирский	1	0	5	6	3
Пассажировместительность, чел.				58	40	32
Парк вагонов		10	8	80	70	30

Определите оптимальное количество пассажирских и скорых поездов, обеспечивающих максимальное количество ежедневно отправляемых пассажиров с вокзала.

Вариант 9. Малое предприятие арендовало мини-пекарню для производства чебуреков и беляшей. Мощность пекарни позволяет выпускать в день не более 50 кг продукции. Ежедневный спрос на чебуреки не превышает 260 штук, а на беляши — 240 штук. Суточные запасы теста и мяса и расходы на производство каждой единицы продукции приведены в таблице. Определить оптимальный план ежедневного производства чебуреков и беляшей, обеспечивающих максимальную выручку от продажи.

	Расход на производство, кг/шт.		Суточные запасы сырья, кг
	чебурека	беляша
Мясо	0,35	0,6	21
Тесто	0,65	0,3	22
Цена, руб./кг	50,0	80,0

Вариант 10. Издательский дом «Геоцентр-Медиа» издает два журнала: «Автомеханик» и «Инструмент», которые печатаются в трех типографиях: «Алмаз-Пресс», «Карелия-Принт» и «Hansaprint» (Финляндия), где общее количество часов отведенное для печати и производительность печати одной тысячи экземпляров ограничены и представлены в следующей таблице:

Типография	Время печати одной тысячи экземпляров		Ресурс времени, отведенный типографией, ч
	«Автомеханик»	«Инструмент»
Алмаз-Пресс	2	14	112
Карелия-Принт	4	6	70
Hansaprint	6	4	80
Оптовая цена, руб./шт.	16	12

Спрос на журнал «Автомеханик» составляет 12 тысяч экземпляров, а на журнал «Инструмент» — не более 7,5 тысячи экземпляров в месяц.

Определите оптимальное количество издаваемых журналов, которые обеспечат максимальную выручку от продажи.