лабы информатика. Методические указания по выполнению лабораторных работ для студентов фэуб специальностей 080200 Менеджмент
 Скачать 10 Mb.
|
|
ЗАДАЧА 2. С Курского вокзала города Москвы ежедневно отправляются скорые и пассажирские поезда. Пассажировместимость и количество вагонов железнодорожного депо станции отправления известны. Определите оптимальное количество пассажирских и скорых поездов, обеспечивающих максимальное количество ежедневно отправляемых пассажиров с вокзала. Рекомендация. x – кол-во скорых поездов, y – кол-во пассажирских. Для того, чтобы узнать количество пассажиров отправляемых ежедневно, необходимо вычислить количество используемых вагонов. ЗАДАЧА 3. Фирма производит два безалкогольных широко популярных напитка «Колокольчик» и «Буратино». Для производства 1л «Колокольчика» требуется 0,02 ч работы оборудования, а для «Буратино» - 0,04ч, а расход специального ингредиента на них составляет 0,01кг и 0,04кг на 1л соответственно. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24ч работы оборудования. Доход от продажи 1л «Колокольчика» составляет 0,25 руб., а «Буратино» - 0,35 руб. Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи. Ответ: Макс. доход 270 руб. ЗАДАЧА 4. Малое предприятие арендовало минипекарню для производства чебуреков и беляшей. Мощность пекарни позволяет выпускать в день не более 50 кг продукции. Ежедневный спрос на чебуреки не превышает 260 штук, а на беляши – 240 штук. Суточные запасы теста и мяса и расходы на производство каждой единицы продукции приведены в таблице. Определить оптимальный план ежедневного производства чебуреков и беляшей, обеспечивающих максимальную выручку от продажи. Ответ: Цел. функция =2880 кг.
ЗАДАЧА 5. Коммерческие расчеты, проведенные студентами в деревне, привели к более выгодному использованию плодов яблок и груш путем их засушки и последующей продажи зимой в виде смеси сухофруктов, варианты которых представлены в таблице. Изучение спроса в магазине «Вишенка» показало, что в день продавалось 18 упаковок смеси 1 и 54 упаковки смеси 2. Из 1кг свежих яблок получается 200г сушеных, из 1кг свежих груш – 250г сушеных. Определить оптимальное количество упаковок сухофруктов по 1кг смесей первого и второго вида, обеспечивающее максимальный ежедневный доход от продажи.
Ответ: Доход=380 руб. ЗАДАЧА 6. Имеются четыре вида работ и четверо рабочих. Затраты каждого рабочего на каждую работу в условных единицах приведены в таблице. Каждый рабочий может выполнять только одну работу и каждая работа выполняется только один раз. Требуется минимизировать общие затраты. Таблица 1. Затраты на работы
Для успешного решения задачи создадим вспомогательную таблицу загрузки рабочих (см. рис.), в которой с помощью 0 и 1 фиксируются выполняемые каждым рабочим работы. Если данная работа выполняется рабочим, то в соответствующей ячейке - 1, иначе - 0. Эта таблица должна обладать свойствами: 1) Значения в ячейках должны принимать только два целочисленных значения 0 или 1, 2) Суммы строк и столбцов должны принимать значение равное 1. Таблица 2. Загрузка рабочих
В качестве целевой функции для перемножения и суммирования элементов массивов удобно использовать функцию суммы произведений, в качестве аргументов которой использовать два диапазона: таблицу затрат и таблицу загрузки. Например, СУММПРОИЗВ(В2:Е5;А8:D11). Для ограничений на 0 и 1 в ячейках таблицы загрузки удобно использовать двоичные значения. В результате решения получим ответ на то, какой рабочий какую работу выполняет и минимальные суммарные затраты равные 18 условным единицам – (проверить). Лабораторная работа №6 Транспортная задача линейного программирования Цель работы: научиться решать транспортные задачи и задачи распределения ресурсов в среде MS Excel Содержание работы: 1. Изучение видов транспортной задачи и методов её решения. 2. Изучение видов распределительной задачи и методов её решения. Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических разработках и практическом применении на транспорте ив промышленности. Особенно большое значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта. Транспортная задача – это задача, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям. Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции. Пример 1. Три поставщика одного и того же продукта располагают в планируемый период следующими запасами этого продукта: первый- 120 условных единиц, второй- 100 и третий 80 единиц. Этот продукт должен быть перевезен к трем потребителям, спросы которых соответственно равны 90, 90 и 120 условных единиц. Приведенная ниже таблица содержит показатели затрат, связанных с перевозкой продукта из i-го пункта отправления в j-й пункт потребления. Требуется перевезти продукт с минимальными затратами.
1 Составим математическую модель задачи. Пусть  –I поставщиком, А-му потребителю, тогда  ,  – количество единиц продукта перевозимого этим же поставщиком Б-му и В-му потребителю соответственно.Целевая функция в этом случае имеет вид:  При следующих ограничениях (первые три ограничения – по запасам продуктов, последние три – по спросу потребителей): 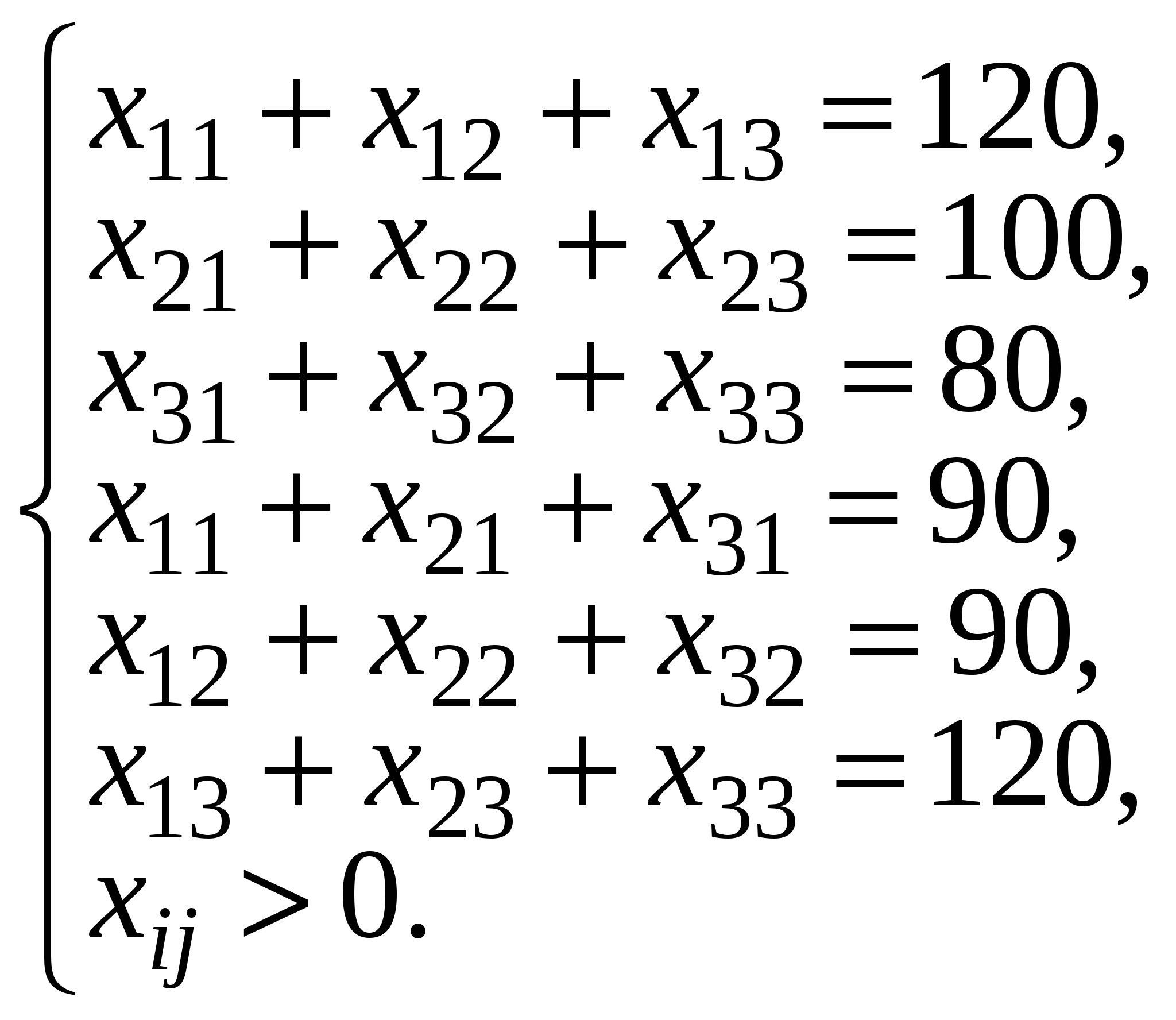 2 Решение задачи в программе "Поиск решения" Вид электронной таблицы Excel, созданной для решения задачи, в режиме отображения формул, представлен на рис. 1. Искомые значения  находятся в блоке ячеек B4:D6. Адрес данного блока входит в поле ввода Изменяя ячейки в окне “Поиск решения”. Требования к ограничениям по спросу и запасам представлены соответственно в ячейках B7:D7 и E4:E6. Коэффициенты ЦФ, означающие затраты на доставку расположены в блоке ячеек B12:D14.Формулы целевой функции и ограничений находятся соответственно в ячейке F8 и ячейках B8:D8 (ограничения по спросу), F4:F6 (ограничения по запасам). 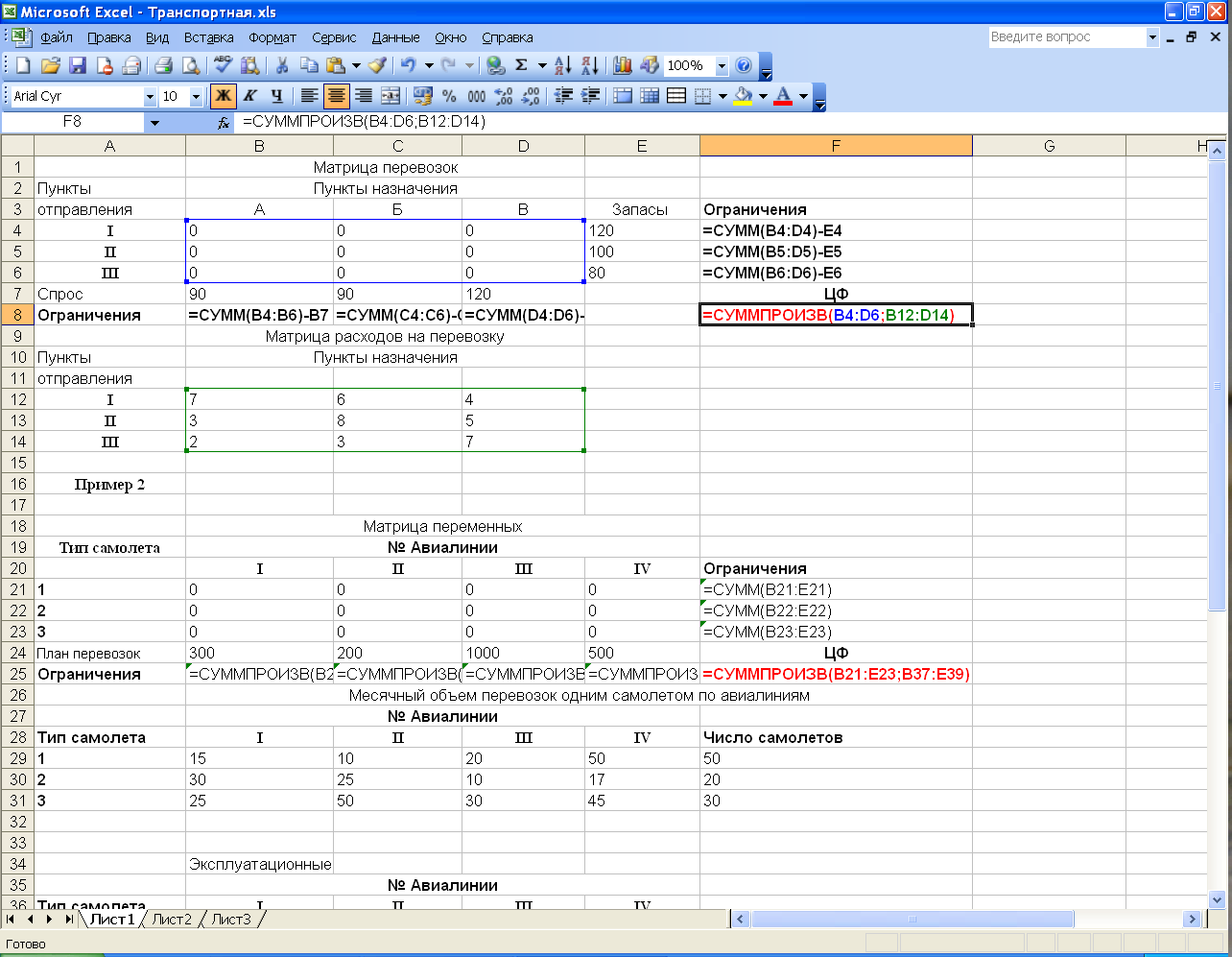 Рис.1 Результаты поиска решения представлены на рис. 2. Значение ЦФ=1060. 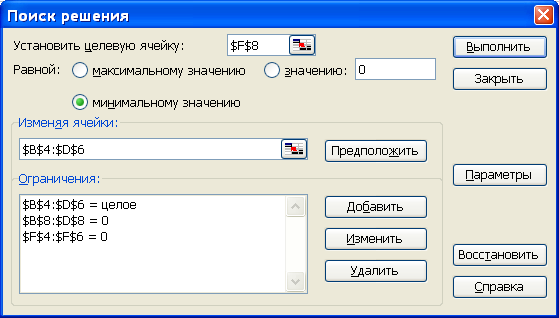 Рис. 2 Данная задача является сбалансированной, в ней общее наличие продукта у поставщиков равно общей потребности в продукте потребителей. На практике возможны случаи, когда эти параметры не совпадают. Тогда в рассмотрение вводятся фиктивная фабрика или фиктивный магазин, которые позволяют свести задачу к сбалансированной. Методом транспортной задачи решаются экономические задачи, которые по своему характеру не имеют ничего общего с транспортировкой груза, поэтому коэффициенты целевой функции могут иметь различный смысл (в зависимости от конкретной задачи. Они могут означать стоимость, расстояние время, производительность и т. д. Рассмотрим постановку и математические модели некоторых задач. Пример 2. Три типа самолетов требуется распределить между четырьмя авиалиниями. В приводимых ниже таблицах задано число самолетов каждого типа, месячный объем перевозок каждым самолетом на каждой авиалинии и соответствующие эксплуатационные расходы. Требуется распределить самолеты по авиалиниям так, чтобы при минимальных суммарных эксплуатационных расходах перевезти по каждой из четырех авиалиний соответственно не менее 300, 200, 1000 и 500 единиц груза.
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:  Ограничения имеют вид: 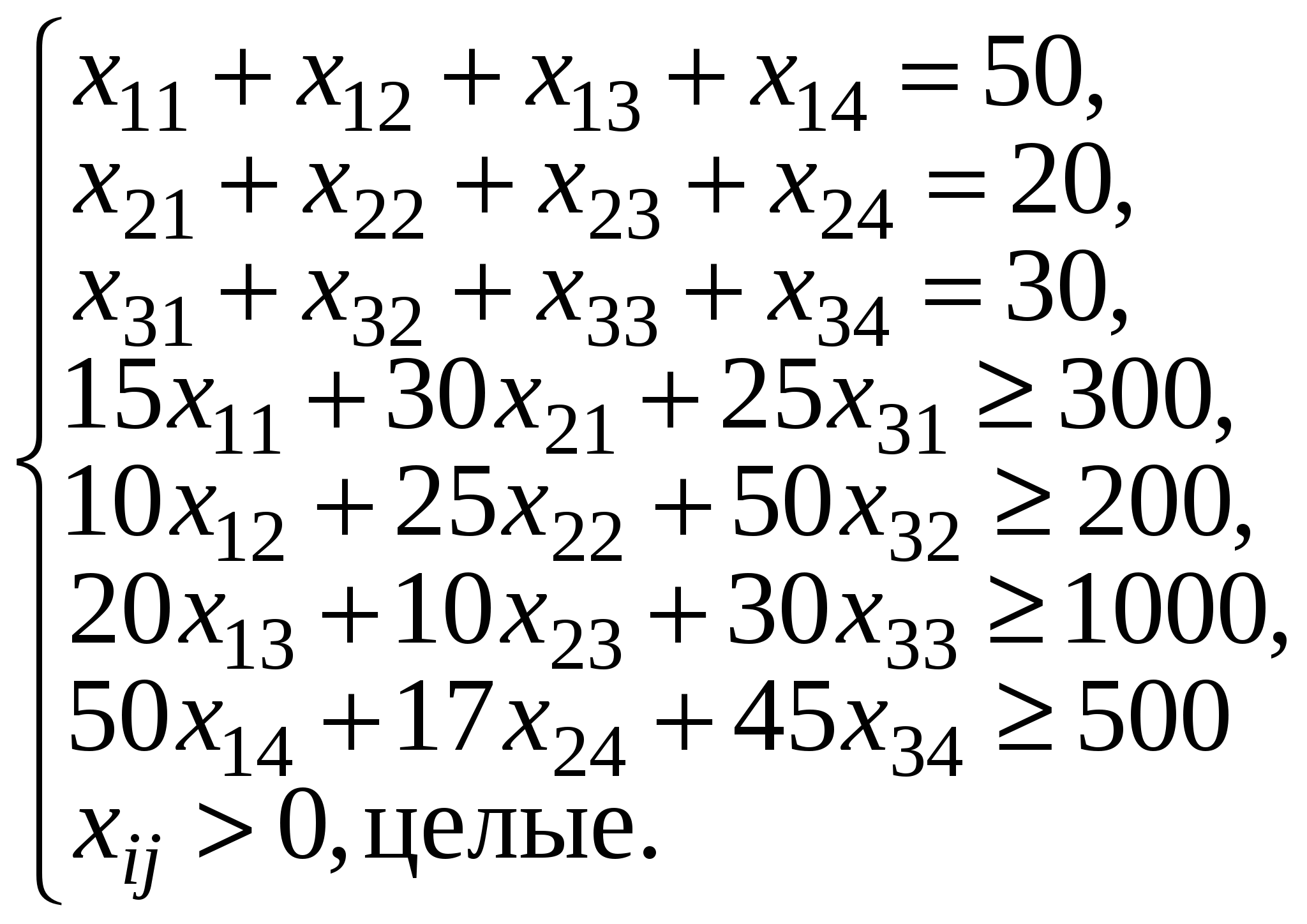 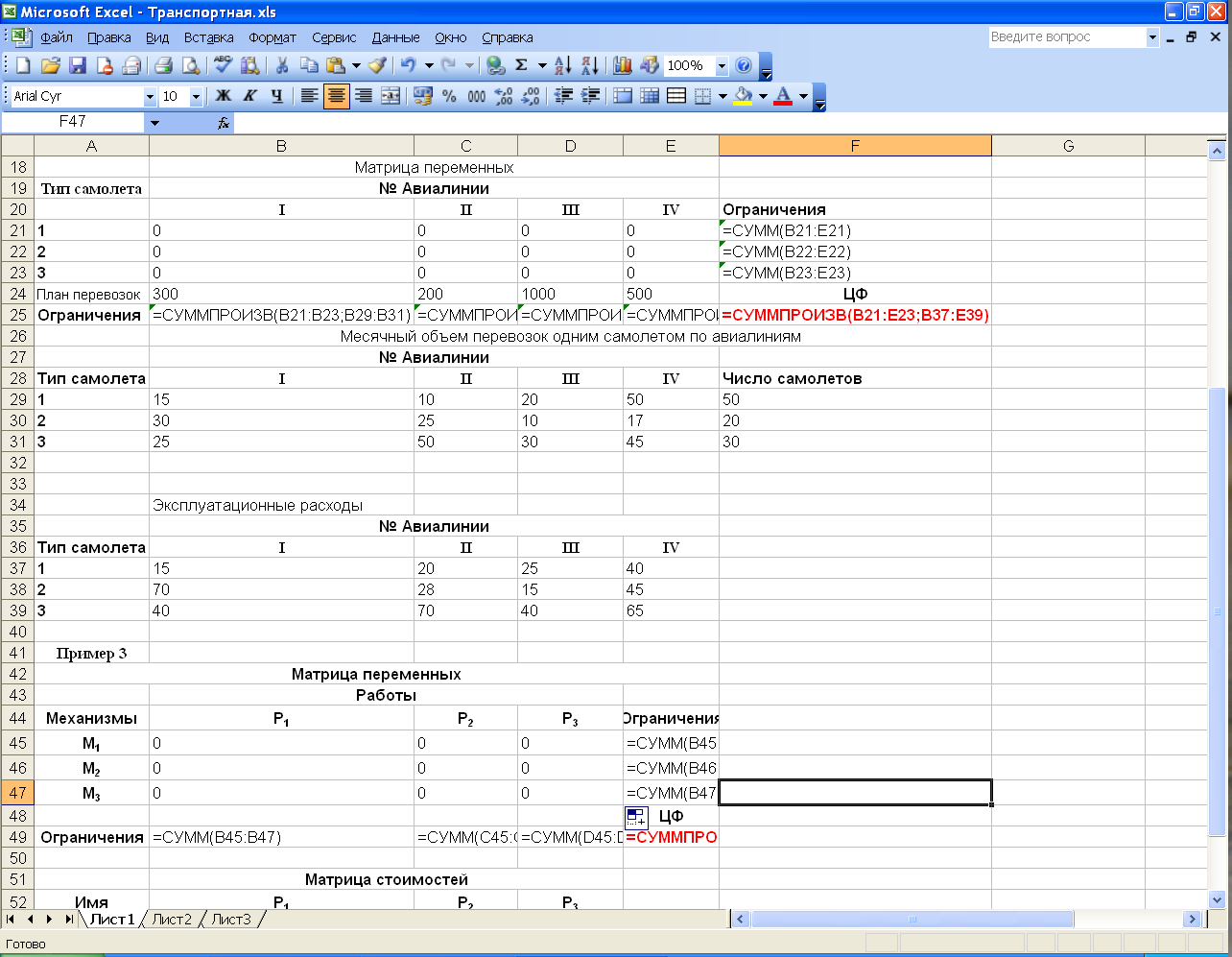 Рис. 3 Вид электронной таблицы Excel, созданной для решения задачи, в режиме отображения формул, представлен на рис. 3. Значения переменных 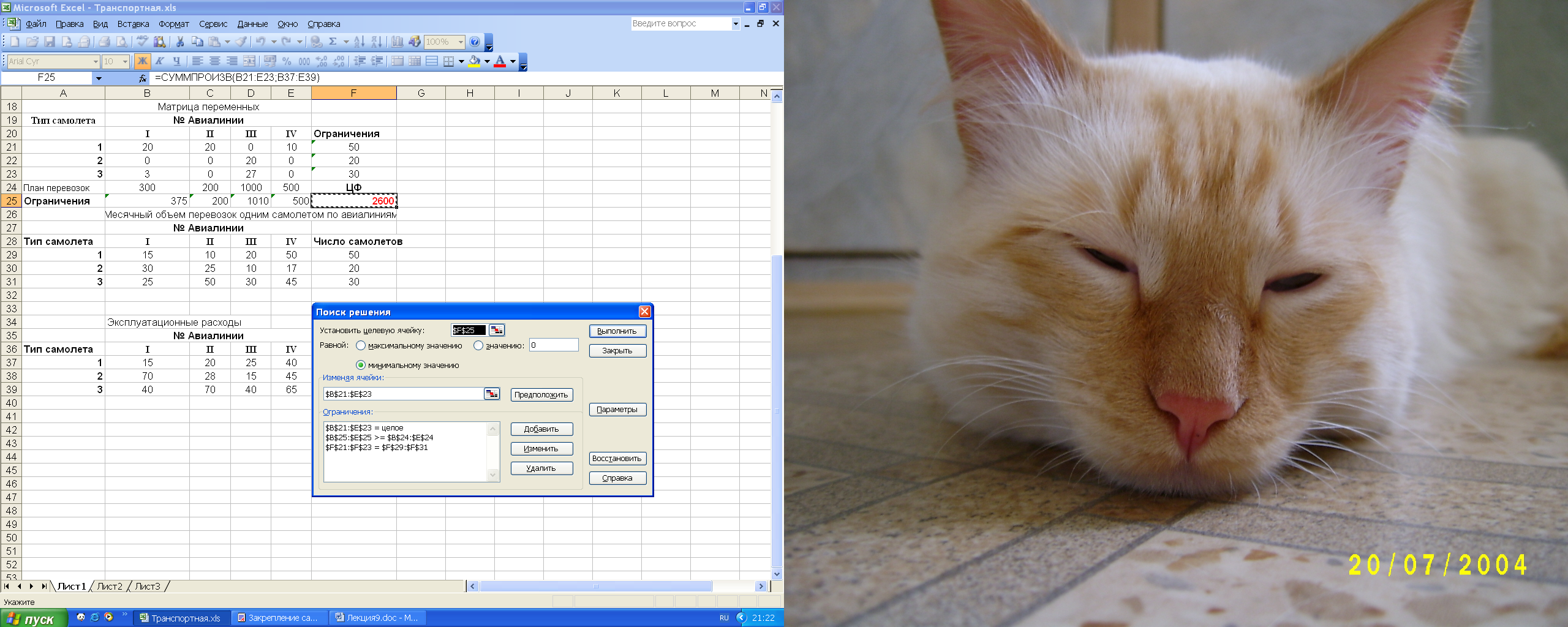располагаются в блоке ячеек B21:E23. Коэффициенты целевой функции, отражающие расходы на перевозку находятся по адресам B37:E39. Данные о месячных объемах перевозок одним самолетом имеются в блоке B29:E31. Задан план перевозок и число самолетов – соответственно блоки B24:E24 и F21:F21. Формулы целевой функции и ограничений находятся соответственно в ячейке F25 и ячейках B25:E25 (ограничения по плану), F21:F23 (ограничения по количеству самолетов). Результаты поиска решения приведены на рис. 4. Рис.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||