Диплом. Министерство образования

• Название: Министерство образования
• Дата: 21.10.2022
• Размер: 5.27 Mb.
• Имя файла: Диплом.docx
• Тип: Урок; #746919
• страница: 4 из 10

1.3. Методические аспекты формирования вычислительных навыков у младших школьников

Одной из основных задач обучения математике на I ступени общего среднего образования является формирование у учащихся вычислительных навыков, обеспечивающих овладение математическим инструментарием для изучения других дисциплин и применения для решения практических проблем.

Проблеме формирования у учащихся вычислительных умений и навыков посвящены исследования М.А. Бантовой, Е.С. Дубинчук, О.А. Ивашовой,  Н. Б. Истоминой, С.С. Минаевой, М.И. Моро, Н.Л. Стефановой, А.А. Столяра,  С.Е. Царевой, Я.Ф. Чекмарёва и др.

На I ступени общего среднего образования учащиеся сначала осваивают приёмы устных вычислений, затем приобретают прочные навыки. «Овладение навыками устных вычислений имеет большое образовательное, воспитательное и практическое значение. Они помогают усвоить многие вопросы теории арифметических действий» [15]. Так, у младших школьников формируются представления о конкретном смысле арифметических действий, свойствах действий, связи между результатами и компонентами, изменением результатов действий в зависимости от изменений одного из компонентов.

Устный счет имеет широкое практическое значение в повседневной жизни: он развивает мышление детей, вызывая у них необходимость, подбирать приемы вычислений, удобные для данного конкретного случая. Устный счёт служит основой для письменных вычислений и помогает лучшему их усвоению, так как последние включают в себя элементы устных вычислений. «Быстрота и правильность устных вычислений особенно необходимы, когда письменно выполнить действия не представляется возможным» [2].

Именно в первые годы обучения закладываются основные приёмы устных вычислений, которые активизируют мыслительную деятельность учеников, развивают у детей память, речь, способность воспринимать на слух сказанное, повышают внимание и быстроту реакции [2].

Вычислительный навык – это вычислительный приём, доведенный до автоматизма или высокая степень овладения вычислительным приёмом. Приобрести вычислительные навыки - значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, причём выполнять эти операции достаточно быстро.

Работа над формированием вычислительного навыка начинается с освоения вычислительного приёма и проходит в несколько этапов: подготовка к введению приёма; ознакомление с новым вычислительным приёмом; формулировка способа действия; закрепление приёма и выработка вычислительного навыка.

Для достижения правильности и беглости устных вычислений в течение всех четырех лет обучения на каждом уроке математики необходимо выделять 5-10 минут для проведения упражнений, предусмотренных программой каждого класса. Навыки устных вычислений формируются в процессе выполнения детьми разнообразных упражнений, связанных как с нахождением значения числового выражения, так и в процессе решения текстовых задач.

Включая устные упражнения в уроки математики, необходимо их логически связывать не только с темой урока, но и с жизненными ситуациями, с которыми обучающиеся сталкиваются в окружающем мире. Это позволит им лучше понять учебный материал, а в жизни научиться находить новые взаимосвязи и закономерности [4].

В методической литературе выделяют следующие цели устного счёта как этапа урока:

— достижение поставленных целей урока;

— формирование вычислительных навыков;

— развитие математической культуры, речи;

— умение обобщать и систематизировать, переносить полученные знания на новые задания [10].

При отборе материала для организации устного счёта необходимо придерживаться следующих требований:

1. 
   Упражнения для устного счета выбираются не случайно, а целенаправленно, обеспечивая достижение цели урока.
   
2. 
   Задания должны быть разнообразными, не слишком лёгкими, но и не слишком «громоздкими».
   
3. 
   Тексты упражнений, чертежей и записей должны быть приготовлены заранее.
   
4. 
   К устному счету должны привлекаться все учащиеся.
   
5. 
   При проведении устного счёта должны быть продуманы критерии оценки (поощрение).
   
6. 
   Упражнения должны соответствовать требованиям учебной программы по математике.
   

Рассмотрим примеры заданий:

• 
  Домино (рис.1.1.)
  

рис. 1.1.

В 1 классе хорошо использовать домино. Работа с ним способствует формированию навыков табличного сложения и вычитания в пределах 10, а также знанию соответствующих случаев состава чисел. Работа с "домино" проводится с постепенным повышением трудностей.

Представленное на картинке домино закрепляет у детей умения на соотнесение количества предметов с цифрой.

• 
  Счетные закладки (абак) (рис. 1.2.)
  

рис. 1.2.

Это пособие позволяет первоклассникам не только производить сложение и вычитание, но и сравнивать число.

Например, можно попросить детей показать сложить 12 и 20 на абаке. Для этого детям задаются такие вопросы: «Сколько десятков в числе 12?», «Сколько единиц?». Дети же сами откладывают нужное количество кругов на ленте десятков и единиц. Таким же образом проводится работа с абаком по сложению и вычитанию чисел.

• 
  Числовой веер (рис. 1.3.)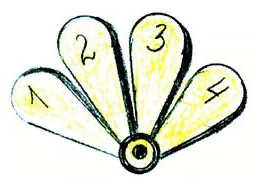
  

рис. 1.3.

Хорошо использовать при проведении математического диктанта в 1-2 классах. Сам же диктант активизирует внимание и мышление детей, способствует формированию вычислительных навыков.

• 
  Ромашка (рис. 1.4.)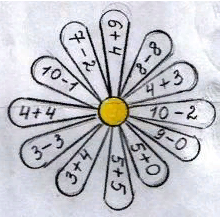
  

рис. 1.4.

На лепестках цветка написаны числа от 1 до 10, а в середине знак (+, -) (x, : ) и прорезь, куда вставляются числа. Это пособие помогает проводить игру "Молчанка".

• 
  Кошка (рис. 1.5.)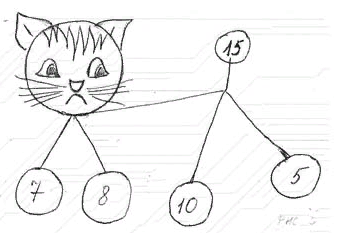
  

рис. 1.5.

Хорошо применять при изучении сложения и вычисления, умножения и деления как табличных, так и внетабличных случаев.

На листе ватмана нарисована кошка. Кружки - это кармашки для цифр, они должны быть прозрачными. В 1 классе при изучении темы "Нумерация чисел от 1 до 10" дети усваивают все случаи состава чисел в пределах 10. Например, состав числа 8. Число 8 вставляют в красный кружок, на хвосте, а числа 5, 3, 6, 2 и т.д. в кружки на лапках. Дети отвечают: 8 - это 5 и 3, 6 и 2 и т.д. Во 2 классе включаю табличные случаи умножения и деления. Спрашиваю, как можно найти число 6. Дети отвечают 6- это частное чисел 12 и 2, 18 и 3, произведения 2 и 3, разность 18 и 12. И таких заданий можно придумать неограниченное число.

• 
  Задачи в стихах
  

При проведении устного счёта так же можно использовать задачи в стихотворной форме. Эти упражнения оживляют работу класса, вносят элементы занимательности. Рифмованные задачи помогают усваивать таблицы сложения и вычитания, умножения и деления.

В начальных классах важно систематически тренировать учащихся в устном решении примеров. Для этого используют карточки, покрытые целлофаном:

1. 
   Лесенка
   
2. 
   Лабиринт
   

На карточках могут быть написаны различные задания, но главное, что прозрачность целлофановой плёнки даёт возможность их использовать несколько раз. Изготовление их занимает меньше времени. Работа с карточками способствует лучшему усвоению учебного материала, формированию вычислительных навыков, вызывает интерес к учебе.

Такие задания не только формируют вычислительные навыки, но и развивают устойчивость внимания, увеличивают его объем, учат распределять и переключать его.

Вывод

Формирование вычислительных навыков является одной из основных задач, которые необходимо решать при обучении детей в начальной школе, поскольку вычислительные навыки необходимы при изучении арифметических операций. Устные вычисления способствуют развитию мышления учащихся, их сообразительность, математической зоркости и наблюдательности. Следовательно, система устных упражнений доказывает свою эффективность - дети становятся активными и заинтересованы заниматься на уроках математики.