|
|
Контрольные по математике 1 курс спо. 1 семестр-1. Нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной)
Практическая работа № 9
Тема: Декартова система координат в пространстве. Уравнение окружности, сферы, плоскости. Расстояние между точками
Продолжительность: 1 час
Материалы для подготовки к практической работе:
Конспект лекции по теме;
Материалы учебника М.И. Башмакова Математика Глава 5 Занятие 1;
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Координаты в пространстве. Система координат: https://resh.edu.ru/subject/lesson/5724/main/21896/
Образец работы:
Вариант 1
|
Вариант 2
|
(2 балла) Задание 1. Найдите расстояние от точки А до точки В.
|
А(1; 2; -3); В(0; -1; 1)
|
А(3; -2; 1); В(-1; 1; 0)
|
(4 балла) Задание 2. Отрезок, концы которого расположены в точках А и В, разделён на 4 равных части. Найдите координаты точек деления.
|
А(12;-4;3), В(-16;0;8)
|
А(-16;0;4), В(8;-4;2)
|
(2 балла) Задание 3. Напишите уравнение одной из плоскостей, проходящей через точку
|
Р(-6, 1, -4).
|
Q(1, 2, -5).
|
(2 балла) Задание 4. Запишите уравнение
|
сферы с центром в т.А(2;1;-5) и радиусом 5
|
сферы с центром в т.А(2;-5;1) и радиусом 3
|
|
Критерии оценивания:
Оценка
|
Баллы
|
5
|
9-10
|
4
|
7 – менее 9
|
3
|
5 – менее 7
|
2
|
менее 5
|
|
Образец выполнения работы:
Задание 1. Найдите расстояние от точки А до точки В, если А(7; 4; -3); В(2; -2; 0).
Решение:
Дано:А(7; 4; -3); В(2; -2; 0)
Найти: расстояние от А до В
Решение:
Для того, чтобы найти расстояние между точками А и В, воспользуемся формулой:
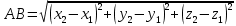
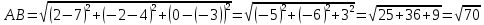
Ответ: 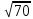 . .
|
Задание 2. Отрезок, концы которого расположены в точках А и В, разделён на 4 равных части. Найдите координаты точек деления.А(16; 20; -10), В(-4; 10; 0)
Решение:
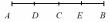
|
Дано: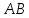 – отрезок – отрезок
А(16; 20; –10), В(–4; 10; 0)
AD=DC=CE=EB
Найти: координаты С, D, E
|
Решение:
C – середина AB. Найдем координаты точки С по формулам:
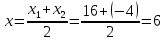
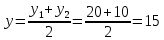
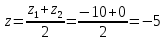
C(6; 15; –5)
D– середина AC. Найдем координаты точки D по формулам:
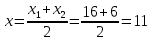
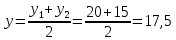
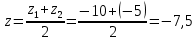
D(11; 17,5; –7,5)
E – серединаCB. Найдем координаты точки С по формулам:
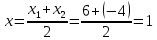
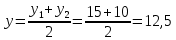
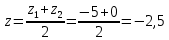
E(1; 12,5; –2,5)
Ответ: C(6; 15; –5), D(11;17,5;–7,5), E(1; 12,5; –2,5)
|
Задание 3. Запишите уравнение сферы с центром в т. А(4; 0; 2) и радиусом 6.
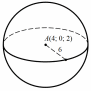
|
Дано: 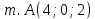 – центр сферы – центр сферы
R=6
Найти: записать уравнение сферы
|
Решение:
Уравнение сферы имеет вид: 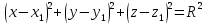 , где , где 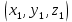 – координаты центра сферы. – координаты центра сферы.
Тогда:
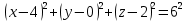
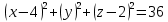 – искомое уравнение – искомое уравнение
Ответ: 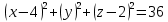
| |
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.
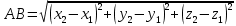
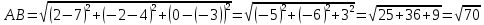
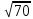 .
.
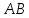 – отрезок
– отрезок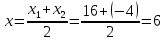
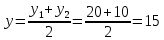
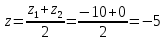
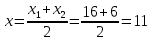
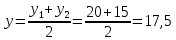
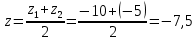
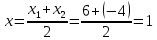
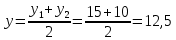
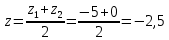

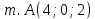 – центр сферы
– центр сферы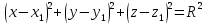 , где
, где 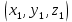 – координаты центра сферы.
– координаты центра сферы.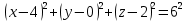
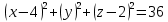 –
–