|
|
Контрольные по математике 1 курс спо. 1 семестр-1. Нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной)
Практическая работа № 10
Тема: Действия с векторами, заданными координатами. Скалярное произведение векторов. Векторное уравнение прямой и плоскости. Использование векторов при доказательстве теорем стереометрии
Продолжительность: 1 час
Материалы для подготовки к практической работе:
Конспект лекции по теме;
Материалы учебника М.И. Башмакова Математика Глава 5 Занятия2-3;
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Скалярное произведение векторов: https://resh.edu.ru/subject/lesson/5723/main/149171/
2. Координатный метод решения задач: https://resh.edu.ru/subject/lesson/6083/main/149233/
Образец работы:
Вариант 1
|
Вариант 2
|
(5 баллов) Задание 1.Векторы 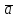 , ,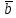 , , 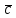 заданы их декартовыми координатами: заданы их декартовыми координатами: 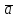 =(1;2;–1), =(1;2;–1), 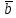 =(3;–1;7), =(3;–1;7), 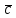 =(0;2;4). Найдите координаты следующих векторов: =(0;2;4). Найдите координаты следующих векторов:
|
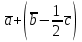 ; ;
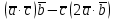 . .
|
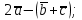
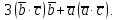
|
(5 баллов) Задание 2. Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ.
|
А(1; 0; –1), В(4; 6; –3)
|
А(3; –4; 5), В(2; 1; –3)
|
|
Критерии оценивания:
Оценка
|
Баллы
|
5
|
6
|
4
|
4 – менее 6
|
3
|
3 – менее 4
|
2
|
менее 3
|
|
Образец выполнения:
Задание 1.Векторы 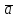 , ,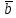 , , 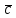 заданы их декартовыми координатами: заданы их декартовыми координатами: 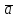 =(6;3;–3), =(6;3;–3), 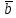 =(2; 1;–1), =(2; 1;–1), 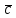 =(0;2;1). Найдите координаты следующих векторов: =(0;2;1). Найдите координаты следующих векторов:
2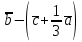 ; ;
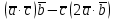 . .
Решение:
Дано: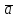 =(6;3;–3), =(6;3;–3), 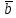 =(2; 1;–1), =(2; 1;–1), 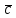 =(0;2;1) =(0;2;1)
Найти: 2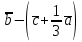 ; ;
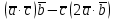 . .
Решение:
1) 2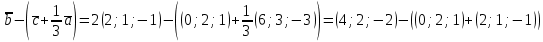 = =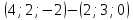 = =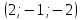
2) 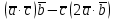 = =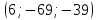
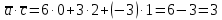
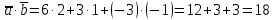
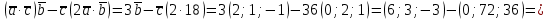
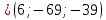
|
Задание 2. Составьте уравнение плоскости, проходящей через точку А(–1, 1, 2) и перпендикулярной прямой АВ, если В(2, 0, 1).
Замечание: Пусть 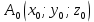 – некоторая точка плоскости. – некоторая точка плоскости.
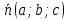 – вектор перпендикулярный плоскости (нормальный вектор), тогда коэффициенты – вектор перпендикулярный плоскости (нормальный вектор), тогда коэффициенты 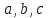 в уравнении плоскости в уравнении плоскости 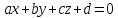 являются координатами вектора являются координатами вектора 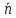 . .
Решение:
|
Дано: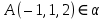
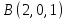
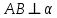
Найти: уравнение плоскости 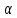
|
Решение:
Уравнение плоскости имеет вид: 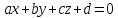 , где , где 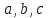 – координаты вектора – координаты вектора
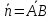 перпендикулярного плоскости. перпендикулярного плоскости.
Найдем координаты нормального вектора:
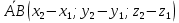
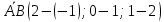
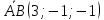
Уравнение плоскости примет вид:
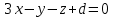
Осталось найти значение 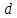 . Подставим в полученное уравнение вместо . Подставим в полученное уравнение вместо 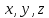 координаты точки координаты точки 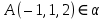 и выполним вычисления: и выполним вычисления:
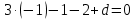
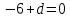
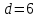
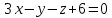 – искомое уравнение плоскости – искомое уравнение плоскости
Ответ: 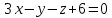 . .
|
|
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.
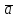 ,
,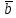 ,
, 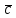 заданы их декартовыми координатами:
заданы их декартовыми координатами: 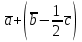 ;
;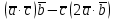 .
.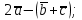
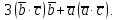
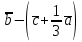 ;
;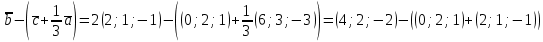 =
=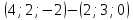 =
=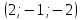
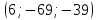
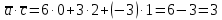
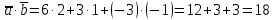
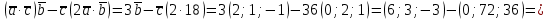
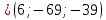
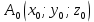 – некоторая точка плоскости.
– некоторая точка плоскости.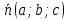 – вектор перпендикулярный плоскости (нормальный вектор), тогда коэффициенты
– вектор перпендикулярный плоскости (нормальный вектор), тогда коэффициенты 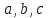 в уравнении плоскости
в уравнении плоскости 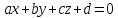 являются координатами вектора
являются координатами вектора 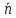 .
.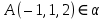
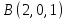
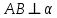
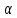
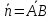 перпендикулярного плоскости.
перпендикулярного плоскости.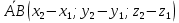
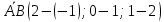
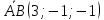
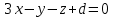
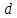 . Подставим в полученное уравнение вместо
. Подставим в полученное уравнение вместо 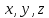 координаты точки
координаты точки 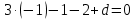
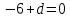
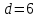
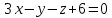 – искомое
– искомое