39 решенных задач по курсу Финансовые вычисления. Наращение по простым процентным ставкам

• Название: Наращение по простым процентным ставкам
• Дата: 30.10.2020
• Размер: 0.66 Mb.
• Имя файла: 39 решенных задач по курсу Финансовые вычисления.doc
• Тип: Задача; #146794
• страница: 8 из 10

8Банковское дисконтирование (банковский учет)

Данная операция применяется при учете векселей. Суть операции заключается в следующем: банк или другое финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (скидкой). При наступлении срока платежа по векселю, банк получает полную сумму, реализуя тем самым процентный доход в виде дисконта.

В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, однако ранее указанного на нем срока.

При учете векселя применяется банковский, или коммерческий, учет. Согласно этому методу проценты за пользование ссудой в виде дисконта (DS) начисляются на сумму, подлежащую уплате в конце срока (FV). При этом применяется специальная ставка, которая называется учетной (d).

8.1Учет по простой учетной ставке

Размер дисконта, или суммы учета, очевидно равен

(14) , где

d ‑ годовая учетная ставка,

n ‑ срок от момента учета до даты погашения в годах.

Таким образом

(15) .

Дисконтный множитель здесь равен

(16) .

Из формулы (15) вытекает, что при n >1/d величина k_д и PV станет отрицательной. Иначе говоря, при относительно большом сроке векселя и (или) большой учетной ставке учет может привести к нулевой или даже отрицательной сумме PV, что лишено смысла.

Учет посредством учетной ставки чаще всего осуществляется при временной базе К = 360 дней, число дней ссуды обычно берется точным (метод 365/360). Однако в практике российских банков на текущий момент чаще применяется метод 365/365.

Для учета при сроках, измеряемых в единицах времени меньше года расчетные формулы имеют вид:

(14.1) ,

(15.1)

(16.1) .

32. 
    Задача
    

Тратта (переводной вексель) выдан на сумму 100 тыс. руб. с уплатой 17 ноября 2006г. Владелец векселя учел его в банке 23 сентября 2006г. по учетной ставке 20% (метод 365/365). Определить сумму, полученную при учете и доход банка, который он получит при предъявлении векселя.

Решение.

Оставшийся до конца срока период равен 55 дням:

Сентябрь	8
Октябрь	31
Ноябрь	17-1=16
Всего дней:	55

 ‑ сумма, полученная при учете.

 или

 ‑ доход банка.

8.2Учет по сложной учетной ставке

В практике учетных операций иногда применяют сложную учетную ставку. В этих случаях процесс дисконтирования происходит с замедлением, так как каждый раз учетная ставка применяется не к большой конечной сумме (как при простой учетной ставке), а к сумме, уменьшенной дисконтированием на предыдущем шаге. Дисконтирование по сложной учетной ставке осуществляется по формуле

(17) ,  где

d ‑ сложная годовая учетная ставка,

(18) ,

(19) ;

А при периодичности начисления дисконта меньше года:

(17.1) ,  где

f ‑ номинальная годовая учетная ставка,

(18.1) ,

(19.1) .

33. 
    Задача
    

Долговое обязательство на сумму 500 тыс. руб., срок оплаты которого наступает через 18 месяцев, продано с дисконтом по сложной учетной ставке 15% годовых с ежемесячным дисконтированием. Каков размер полученной за долг суммы, величина дисконта и дисконтный множитель. Рассчитать также сумму, которая была бы получена при учете по простой ставке того же размера.

Решение.











При учете по простой учетной ставке получаем

34. 
    Задача
    

Сделать оценку современной стоимости долга, который через семь лет составит сумму 1 млн. руб. используя математическое и банковское дисконтирование по простой и сложной ставке 20% годовых и 120% годовых при ежегодном начислении дисконта.

Решение.

1. Ставка 20% годовых.

1.1. Математическое дисконтирование, простая ставка.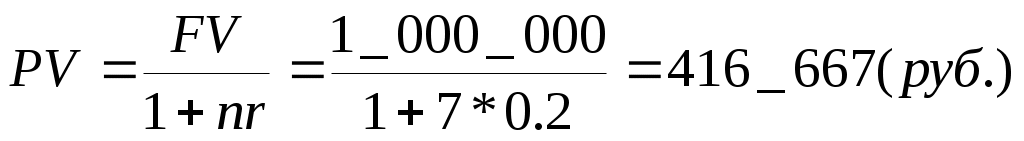



1.2. Математическое дисконтирование, сложная ставка.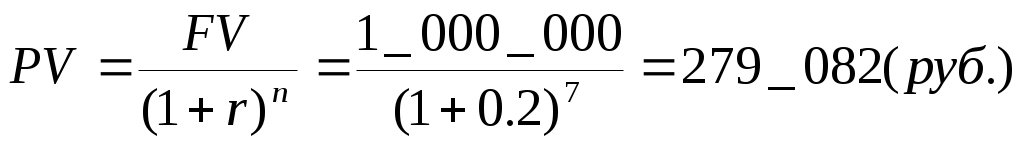



1.3. Банковское дисконтирование, простая ставка.



1.4. Банковское дисконтирование, сложная ставка.



2. Ставка 120% годовых.

2.1. Математическое дисконтирование, простая ставка.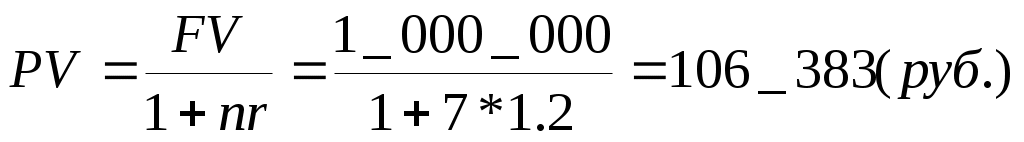



2.2. Математическое дисконтирование, сложная ставка.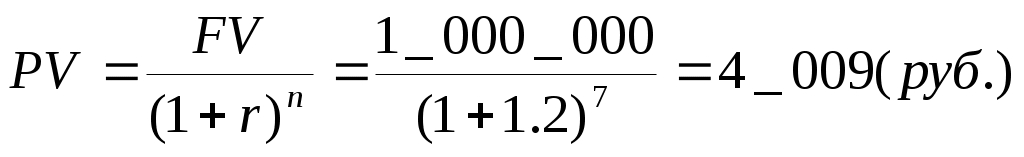



2.3. Банковское дисконтирование, простая ставка.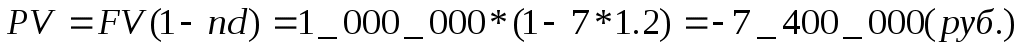



2.4. Банковское дисконтирование, сложная ставка.



Выводы. 1. При математическом дисконтировании по сложной ставке значение PV всегда меньше, чем при математическом дисконтировании по простой ставке (ставки, выраженные в % годовых равны).

2. Банковское дисконтирование в области разумных ставок и сроков дисконтирования, наоборот, дает значение PV меньше в случае применения простой ставки по сравнению со сложной.

3. Банковское дисконтирование является более жестким по сравнению с математическим и всегда дает меньшее значение PV. При больших сроках и (или) ставках зачастую результат банковского дисконтирования приближается к нулю или даже становится отрицательным, что лишено экономического смысла.

Именно поэтому приведение платежей при анализе долгосрочных операций всегда выполняется с применением математического дисконтирования.