39 решенных задач по курсу Финансовые вычисления. Наращение по простым процентным ставкам
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
9Применение дисконтированияОдним из частных случаев применения дисконтирования является сравнение платежей, поступающих в разные моменты времени путем приведения их к одной дате, а также расчет эквивалентных сумм платежей. Приведение осуществляется либо путём дисконтирования к более ранней дате, либо путем наращения к более поздней дате. Сравнение платежей предполагает использование некоторой процентной ставки, которую называют при этом ставкой сравнения (ставкой приведения), полученный результат зависит от выбора её величины. Нетрудно заметить, что с ростом процентной ставки величина PV уменьшается. Таким образом, при некотором ставки будет выполнено равенство PV1=PV2, т.е. современные стоимости платежей совпадут. Платежи, которые оказываются равными при приведении к одному моменту времени, называются эквивалентными, а ставка сравнения в этом случае (r0) называется критической (или барьерной). Уровень этой ставки в случае применения простых процентов может быть вычислен исходя из равенства: (20) 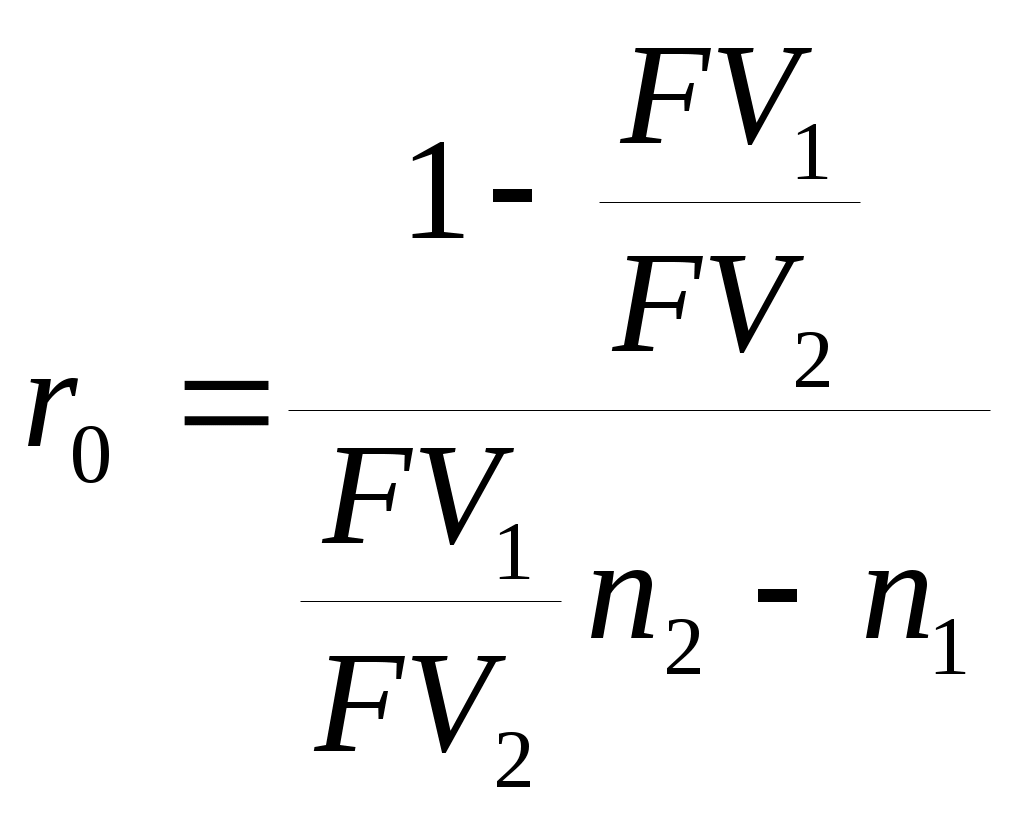 , ,а для случаев, когда период дисконтирования измеряется в единицах времени меньше года: (20.1) 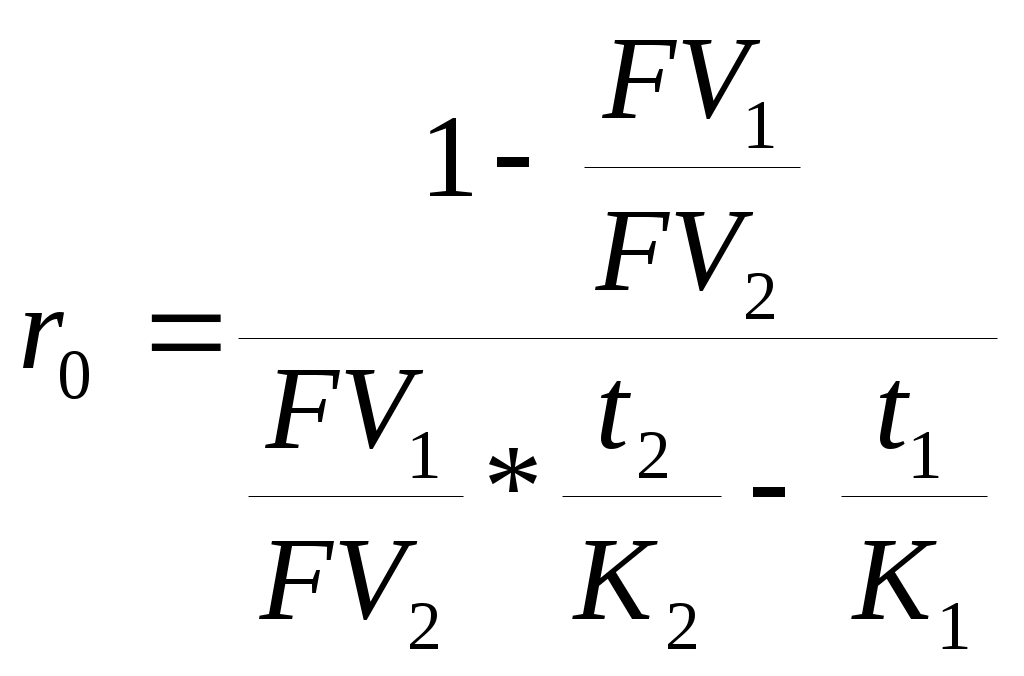 . .При применении сложных процентов формулы расчета барьерной точки выводятся исходя из того же равенства современных стоимостей двух разновременных платежей: 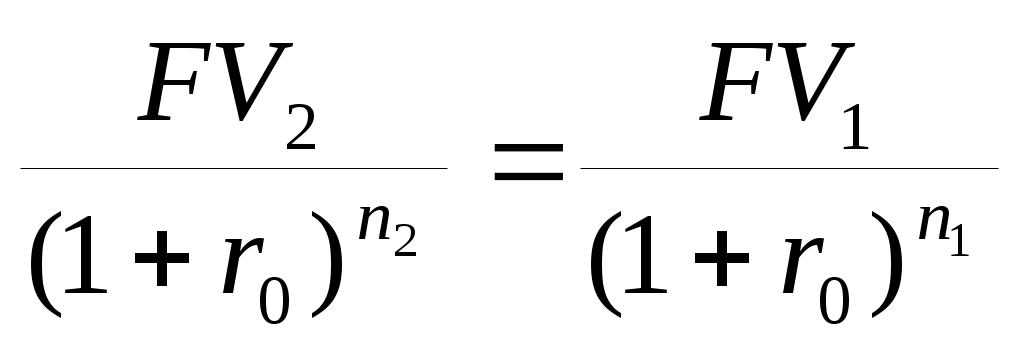 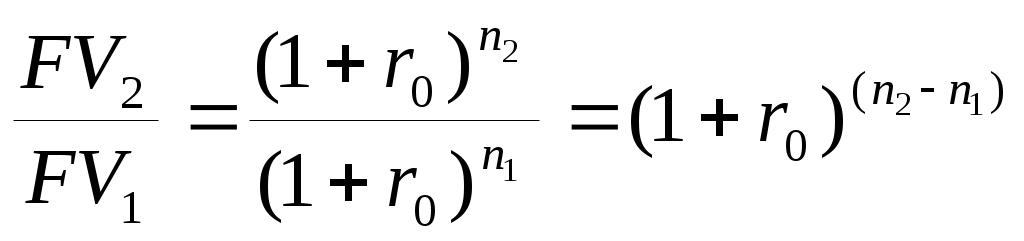 (21) (21.1) 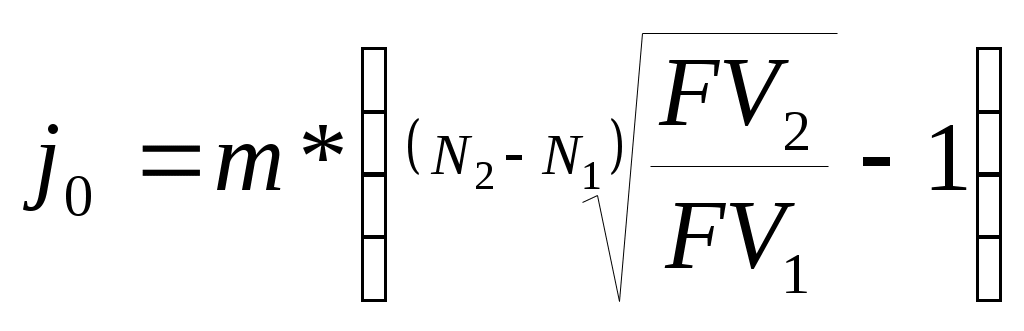 . .Задача Сравнить два платежа: 200 тыс. руб. через 2 года и 230 тыс. руб. через три года при ставках сравнения 10% и 20% годовых (схема – сложные проценты) и найти ставку, при которой платежи эквивалентны (барьерную ставку). 1. Ставка 10% годовых. Вывод. При ставке сравнения 10% годовых второй платеж больше первого. 2. Ставка 20% годовых. Вывод. При ставке сравнения 20% годовых второй платеж меньше первого. 3. Платежи эквивалентны при ставке сравнения (барьерная ставка) Современные финансовые операции часто предполагают совершение не отдельных платежей, а некоторой их последовательности во времени (например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций и т.д.). Каждую такую последовательность называют потоком платежей, а ее отдельные элементы ‑ членами потока. Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке членами являются как положительные (поступления), так и отрицательные величины (выбытия), а соответствующие платежи могут производиться через разные интервалы времени. Члены регулярного потока ‑ либо только поступления средств, либо только их выплаты, причём сами платежи довольно часто (но не всегда) поступают через равные промежутки времени. Современная (настоящая) стоимость потока платежей ‑ сумма всех его членов, уменьшенная (дисконтированная) на величину процентной ставки на определённый момент времени, совпадающий с началом потока платежей, или предшествующий ему. Наращенная (будущая) стоимость потока платежей ‑ сумма всех членов потока платежей с начисленными на них процентами на конец срока, т.е. на дату последней выплаты. Финансовая операция может предусматривать неоднократные и разновременные переходы денежных сумм от одного владельца к другому. Рассматривая поток платежей с позиций одного из них, можно считать все поступления к нему положительными величинами, а все его выплаты ‑ отрицательными. Для оценки финансовой операции в целом используется чистая приведённая величина (net present value, NPV), вычисляемая как сумма всех членов потока, дисконтированная на величину процентной ставки на начальный момент времени. Представим поток платежей в виде графической схемы: С1 С2 С3 С4 С5 Сn __________________________________________________________ … ____ , где t1 t2 t3 t4 t5 tn Сi – платежи, ‑ выбытие денежных средств, ‑ поступление средств, ti – моменты времени, выраженные количеством интервалов начисления процентов. Тогда чистая приведенная величина может быть вычислена по формуле: (22) 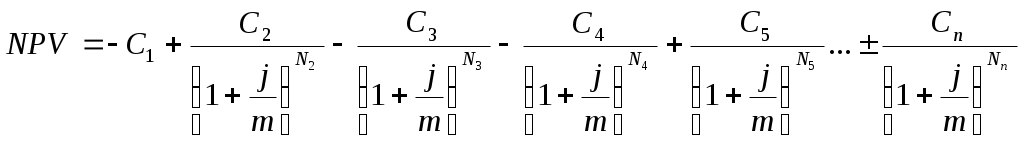 В качестве процентной ставки j, используемой в формуле (22), обычно принимается ставка альтернативного вложения (доходность государственных ценных бумаг или банковская ставка по депозитам с аналогичными сроками), она называется ставкой приведения. При этом начало операции (первая выплата) принимается за начало отсчета времени. Задача Рассчитать NPV потока платежей по данным таблицы. Ставка приведения 15% годовых с ежемесячным начислением. Инвестирование средств и поступления доходов осуществляются в последний день месяца.
Решение. 1. Рассчитываем количество интервалов начисления между датой первой инвестиции и датой каждого из членов потока. 2. Приводим все платежи в потоке к моменту первой инвестиции по формуле (11.1). Для первого члена потока: 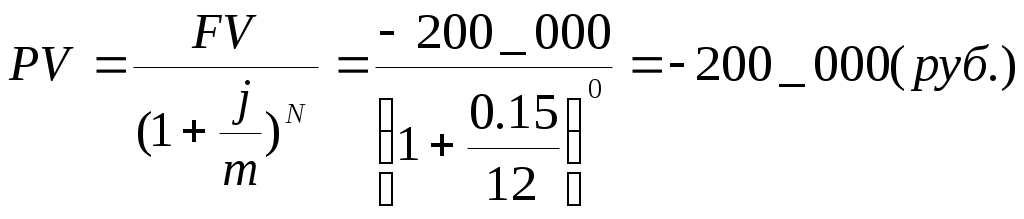
Требование положительности NPV является обязательным при принятии решения о реализации финансовой операции кредитором. Вместе с тем, положительное значение NPV не является достаточным условием для определения степени рациональности и экономической эффективности вложения капитала. С этой целью вводится понятие эффективной ставки операции (внутренней ставки доходности, IRR) как значения ставки процента, при которой NPV окажется равной нулю. При этом аналитический вид зависимости внутренней ставки доходности от временных и числовых параметров членов потока платежей, как правило, не выводится. Задача решается простым подбором значения ставки, при котором NPV становится равным нулю. Если последнюю задачу решить несколько раз, изменяя ставку приведения, то станет очевидным, что при значении ставки 20.285% (20.3%) значение NPV практически становится равным нулю. Таким образом значение 20.3% и является внутренней ставкой доходности инвестиционного проекта (финансовой операции). Выбирая между различными вариантами возможных финансовых операций, инвестор всегда ориентируется на операцию с высшей внутренней ставкой доходности. Задача Данная задача уже решалась ранее (задача 13). Было выяснено, что начисление процентов по условиям договора (методика, часто используемая банками при потребительском кредитовании) приводит к тому, что заемщик переплачивает банку по сравнению с начислением процентов «справедливым» актуарным методом сумму 1 005.55(руб.). 60 тыс. руб. выдано под 20% годовых на условиях потребительского кредита сроком на три месяца. Проценты начисляются на всю сумму первоначального долга методом 360/360 и причисляются к основному долгу в момент открытия кредита. Гашение общей суммы долга производится тремя равными частями по истечении каждого месяца с даты выдачи ссуды. Определить общую сумму гашения, размер ежемесячного платежа и внутреннюю ставку доходности данной финансовой операции для банка. Решение. Сумма процентов за весь срок ссуды: Общая сумма гашения составляет 60 000 + 3 000 = 63 000(руб.) Размер ежемесячного платежа составляет 63 000 / 3 = 21 000(руб.)
Для первого члена потока при ставке приведения 20% годовых: 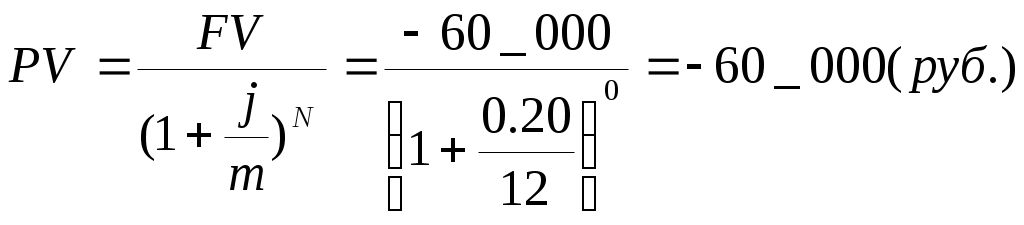 Значение NPV, близкое к нулю, достигается при использовании ставки приведения 29.8% годовых, но это сложная ставка. Поскольку банк объявляет, что кредит выдается под простую ставку 20% годовых, для чистоты эксперимента найдем внутреннюю ставку доходности в простых процентах, для чего продисконтируем члены потока по формуле (8.1): 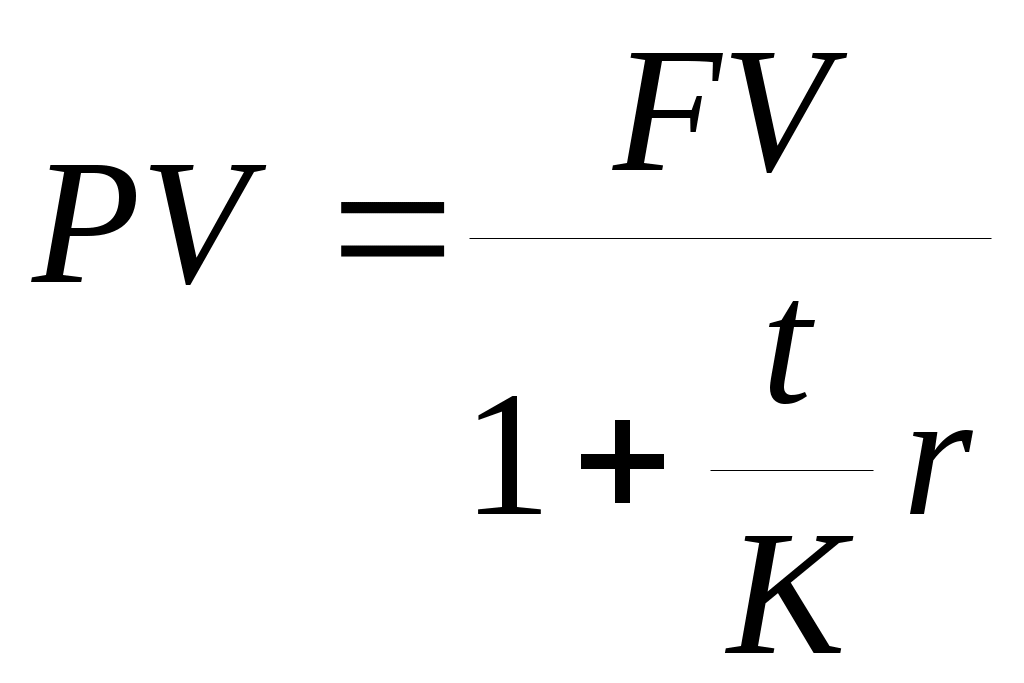
Очевидно, что при дисконтировании по простой ставке, внутренняя ставка доходности кредита для банка еще выше и составляет 30.2% годовых. Значение IRR приближается к объявленной банком процентной ставке в случае, когда проценты начисляются и уплачиваются в соответствии с актуарным методом. В задаче 13 ранее был рассчитан последний платеж при условии начисления процентов актуарным методом, он составил 19 994.45руб. Два первых платежа оставлены без изменений. Определим IRR в этом случае.
Значение IRR для данных условий погашения кредита и процентов по нему составляет приблизительно 20.3%. Оно очень близко к записанной в договоре процентной ставке, но все же больше его. Это объясняется тем, что полученные банком суммы гашения и проценты до момента окончания договора вновь размешаются в кредиты и приносят дополнительный доход. И лишь в одном случае – когда и сам кредит, и проценты по нему гасятся по окончании срока ссуды, объявленная простая процентная ставка и внутренняя ставка доходности совпадают абсолютно:
Данное совпадение ставок объясняется тем, что в этом случае банк не имеет возможности повторного использования ресурсов и получения дополнительного дохода. |
