39 решенных задач по курсу Финансовые вычисления. Наращение по простым процентным ставкам

• Название: Наращение по простым процентным ставкам
• Дата: 30.10.2020
• Размер: 0.66 Mb.
• Имя файла: 39 решенных задач по курсу Финансовые вычисления.doc
• Тип: Задача; #146794
• страница: 5 из 10

4Начисление сложных процентов при дробном числе лет

Часто срок в годах для начисления процентов не является целым числом. В этом случае применяют два метода: общий и смешанный.

1. Согласно общему методу, расчет ведется непосредственно по формулам 4, 5 и 6, при этом показатель степени дробный.

2. Смешанный метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов:

(7)  , где

n = a + b - срок ссуды,

a - целое число лет,

b - дробная часть года.

Аналогичный метод применяется и в случаях, когда интервалом начисления является полугодие, квартал или месяц.

При выборе метода расчета следует иметь в виду, что множитель наращения по смешанному методу оказывается несколько больше, чем по общему, причем наибольшая разница наблюдается при дробной части, равной 0.5.

17. 
    Задача
    

Кредит в размере 3 млн. руб. выдан на 3 года и 160 дней под 16.5% сложных годовых.

Рассчитать сумму долга на конец периода.

Решение.

n = 3 + 160/365 = 3.43836

1. Общий метод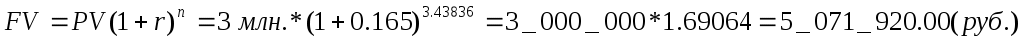

2. Смешанный метод

Вывод. Смешанный метод дает больший результат.

5Начисление сложных процентов несколько раз в году. Номинальная ставка

В современных условиях проценты капитализируются обычно не один, а несколько раз в году – по полугодиям, кварталам, ежемесячно. Для расчета процентов и наращенной суммы в этом случае пользуются модифицированной формулой (4) .

Параметр n в этих условиях будет означать число интервалов начисления, а под ставкой r следует понимать ставку за соответствующий период (не годовую!).

На практике, как правило, в контрактах обычно фиксируется не ставка за интервал начисления, а годовая ставка, которая называется номинальной. Одновременно указывается период начисления процентов. Например, «18% годовых с поквартальным начислением» процентов.

Формулу наращения теперь можно представить следующим образом:

(4.1) , где

m - число интервалов начисления в году,

N = n * m общее число интервалов начисления,

n - продолжительность периода начисления в годах,

j - номинальная ставка наращения, выраженная в долях единицы.

При этом:

(5.1)   - коэффициент наращения.

(6.1)  - сумма начисленных процентов.

18. 
    Задача
    

Какой величины достигнет долг, равный 10 000 руб. через пять лет, при росте по сложной ставке 15.5% годовых и капитализацией процентов раз в год, раз в полугодие, раз в квартал, ежемесячно и ежедневно.

Решение.

Все расчеты проводим по формуле (4.1) .

1. 
   раз в год:
   

2. 
   раз в полугодие:
   

3. 
   раз в квартал:
   

4. 
   раз в месяц:
   

5. 
   ежедневно:
   

Вывод. Чем чаще начисляются сложные проценты, тем быстрее идет процесс наращения, при этом наибольший эффект в увеличении темпа наращения дает переход от ежегодной капитализации к полугодовой, а наименьший – переход от ежемесячной к ежедневной.

19. 
    Задача
    

Вам удалось разместить в очень надежном банке вклад на 1 000 руб. под номинальную ставку 5% годовых сроком на 300 лет с ежемесячной капитализацией. Какую сумму получит ваш правопреемник по окончании срока вклада?

Решение.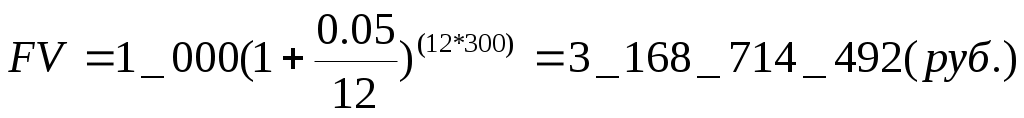



Вывод. Очень большой период начисления сложных процентов с высокой частотой капитализации приводит к устрашающим результатам. Именно поэтому срок действия любых финансовых соглашений всегда ограничен